桶排序算法的思想是:
把待排序数据,按照一定的规则,分配到不同的桶中,使得桶与桶之间形成有序的关系。然后每个桶内再单独排序,这样整个数列就全局有序了。
因此,桶排序的核心要点,包括:
1)桶的数量
2)数据分配到桶的规则
3)桶内排序的算法
桶的数量如果太多,可能会导致有些桶没有数据,白白浪费这些桶的空间。如果桶的数量太少,可能会导致桶内数据太多,桶内排序时间过长。
数据分配到桶的规则,如果与数列不匹配,可能会导致有些桶分配数据过多,有些桶数据很少甚至没有数据的情况发生。
桶内排序的算法,可以使用任意排序算法。
用个例子来说明:
待排序数列为:
8, 35, 13, 29, 16, 30, 2, 22
分配4个桶。
数据分配到桶的规则为:0号桶存放从0到9闭区间的数据,1号桶存放10到19闭区间的数据,2号桶存放20到29闭区间的数据,3号桶存放30及更大的数据。
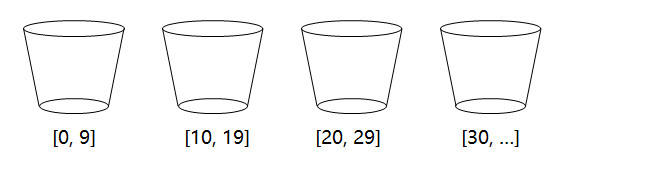
按照数据分配到桶的规则,将待排序数列中的数据,分配到桶:
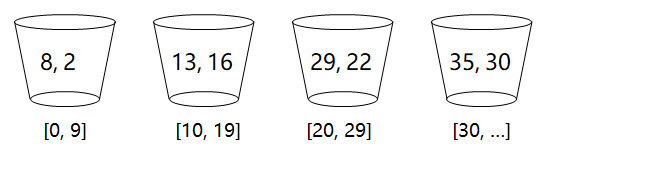
然后每个桶内进行排序:
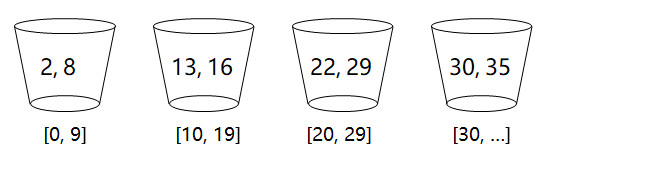
最终,所有桶的数据,就形成了最终排好序的数列。
桶排序算法,C语言实现的代码如下:
(ivec_t 是动态变长数组,存储integer 数据。类似c++中的vector,代码实现见后面)
void bucket_sort(int* parr, int count) {
int bucket_num = 4;
ivec_t* pbuckets = (ivec_t*)malloc(bucket_num * sizeof(ivec_t));
for (int i = 0; i < bucket_num; i++) {
ivec_init(pbuckets + i, 4);
}
// distribute integers to buckets
for (int i = 0; i < count; i++) {
int bucket_idx = parr[i] / 10; // each bucket storage [bucket_idx*10, (bucket_idx+1)*10 - 1]
if (bucket_idx >= bucket_num) {
bucket_idx = bucket_num;
}
ivec_append(pbuckets + bucket_idx, parr[i]);
}
// sort each bucket, store them back to parr
int idx = 0;
for (int i = 0; i < bucket_num; i++) {
ivec_t* pbucket = pbuckets + i;
int* pdata = ivec_buf(pbucket);
int len = ivec_len(pbucket);
if (len > 0) {
quick_sort(pdata, 0, len - 1); // sort bucket
// store them back to parr
for (int k = 0; k < len; k++) {
parr[idx++] = pdata[k];
}
}
}
// destroy buckets
for (int i = 0; i < bucket_num; i++) {
ivec_destroy(pbuckets + i);
}
free(pbuckets);
}
上述代码中,使用了 ivec_t 这样的数据结构及相关函数,实现对桶的数据管理。ivec_t 的实现代码如下:
typedef struct ivec_t {
int cap;
int len;
int* pbuf;
} ivec_t;
int ivec_init(ivec_t* pvec, int cap);
int ivec_append(ivec_t* pvec, int val);
int ivec_len(ivec_t* pvec);
int* ivec_buf(ivec_t* pvec);
int ivec_destroy(ivec_t* pvec);
int ivec_init(ivec_t* pvec, int cap) {
pvec->len = 0;
pvec->cap = cap;
pvec->pbuf = (int*)malloc(cap * sizeof(int));
return 0;
}
int ivec_append(ivec_t* pvec, int val) {
if (pvec->len >= pvec->cap) { // need expand
int new_cap = pvec->cap * 2;
int* pnew_buf = realloc(pvec->pbuf, new_cap * sizeof(int));
if (!pnew_buf) {
return -1;
}
pvec->pbuf = pnew_buf;
pvec->cap = new_cap;
}
pvec->pbuf[pvec->len++] = val;
return 0;
}
int ivec_len(ivec_t* pvec) {
return pvec->len;
}
int* ivec_buf(ivec_t* pvec) {
return pvec->pbuf;
}
int ivec_destroy(ivec_t* pvec) {
free(pvec->pbuf);
memset(pvec, 0, sizeof(*pvec));
return 0;
}
我的微信号是 实力程序员,欢迎大家转发至朋友圈,分享给更多的朋友。





 本文介绍桶排序算法的基本思想,包括桶的数量、数据分配规则和桶内排序算法的选择,并通过实例演示了排序过程。提供了C语言实现代码,展示了如何利用动态数组管理桶数据。
本文介绍桶排序算法的基本思想,包括桶的数量、数据分配规则和桶内排序算法的选择,并通过实例演示了排序过程。提供了C语言实现代码,展示了如何利用动态数组管理桶数据。
















 3353
3353

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








