第8章 基于表格型方法的规划和学习(3) 优先遍历

优先遍历

均匀采样浪费了资源

在 Dyna 类智能体中，规划是指利用内部环境模型生成模拟经验（即模拟的状态转移 $(s,a,r,s^{\prime })$），并通过这些模拟经验更新价值函数，从而在不与真实环境交互的情况下改进策略。 传统方法（如 Dyna-Q）在规划阶段采用均匀采样策略：从所有曾被访问过的“状态-动作”对 $(s,a)$ 中等概率地随机选取一个，使用模型预测其转移结果 $(r,s^{\prime })$，并执行一次价值更新（例如 Q-learning 更新）。然而，这种策略效率低下，因为大多数采样到的更新对当前价值函数几乎不产生实质性影响，其 TD 误差接近于零，导致价值估计无有效改进，却消耗了计算资源。

并非所有“状态-动作”对在当前时刻都值得更新。价值函数的更新仅在能引起有意义的变化时才具有实际效用。然而，均匀采样策略忽略了这一事实，导致大量“无效计算”。例如，假设智能体刚刚首次到达目标状态（即获得正奖励的终止状态）。此时，只有紧邻目标的前一个状态（记为 $s^{\ast }$）在执行某个特定动作 $a^{\ast }$ 时能获得正奖励 $R$。因此，仅有 $Q(s^{\ast },a^{\ast })$ 的值会从初始值（如 0）更新为正值（即 $R$，因为 ${\gamma }^{0}R=R$）。而所有其他状态（尤其是远离目标的区域）的动作价值仍为 0，因为它们尚未通过自举感知到目标的存在。若在此时从所有历史经历过的 $(s,a)$ 对中进行均匀采样以执行模拟更新，绝大多数采样到的转移将导向价值仍为 0 的后继状态 $s^{\prime }$。其对应的 TD 目标为：
$$R+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })=0,$$
与当前估计 $Q(s,a)=0$ 一致，因此 Q-learning 更新结果为：
$$Q(s,a)\leftarrow Q(s,a)+\alpha (0-0)=Q(s,a),$$
不产生任何变化。这类更新徒耗计算资源，却对策略改进毫无贡献。

随着智能体与环境交互的增多，它会逐步发现通往目标的路径。价值信息从目标状态开始，通过自举逐步向远处的状态传播：例如，目标前一步的状态首先获得正价值；随后，目标前两步的状态在后续更新中也能获得正价值；依此类推，形成一个不断向外扩展的有效更新区域。随着时间推移，越来越多的状态-动作对变得值得更新。然而，尽管有效区域持续扩大，均匀采样策略无法识别哪些 $(s,a)$ 对当前最具信息价值。它仍然以相同的概率对所有历史经历过的状态-动作对进行采样。在大规模状态空间中，这种盲目采样方式极其低效。

反向聚焦

在迷宫等任务中，从终点（目标状态）反向传播价值信息能够显著缩小需要更新的状态范围。然而，大多数实际强化学习问题并不显式指定目标状态。例如，奖励函数可能在多个状态上非零，或奖励稀疏且分布广泛。因此，需要一种不依赖于目标状态假设、适用于任意奖励结构的通用规划机制。 在此背景下，目标状态仅作为一个启发性的特例，用于直观理解价值传播的方向性，进而引导设计更普适的高效规划算法。

当任意状态 $s$ 的价值估计发生显著变化（无论增加或减少），该状态即被视为一个信息更新源。此时，应反向追溯所有能一步转移到 $s$ 的前驱状态-动作对 $(\bar{s},\bar{a})$。由于这些前驱对的价值估计依赖于 $s$ 的新价值，因此应优先对其进行更新。更新后，若某前驱的价值也发生显著变化，则继续将其作为新的更新源，反向传播至其自身的前驱；该过程持续进行，直至价值变化低于预设阈值或不存在前驱状态为止，此时信息传播自然终止。

并非所有状态都需要立即更新。唯一有用的单步更新，是那些其后继状态价值已发生变化的状态-动作对。通过这种链式的反向更新机制，价值变化的影响得以高效且有序地扩散至相关区域。这种从价值发生变化的状态出发，反向逐层更新其前驱的规划策略，称为 反向聚焦。

反向聚焦适用于任意奖励函数和任意价值变化源（例如新发现的高奖励、环境动态改变等），不依赖于任务是否具有明确的目标状态，为优先级遍历等高效规划算法提供了理论基础。该策略从价值发生变化的状态出发，进行反向传播式更新，仅更新那些其后继状态价值已发生变化的状态-动作对。若某状态的价值发生改变，则其前驱状态（即存在某个动作 $\bar{a}$，使得执行 $\bar{a}$ 后能一步转移到该状态的状态 $\bar{s}$）的价值估计也可能需要修正。此过程递归进行，沿反向路径逐层传播，直至价值变化的影响衰减至可忽略程度或无前驱可追溯为止。

优先级遍历算法

优先级遍历是反向聚焦思想的具体实现。当价值函数在某个状态发生显著变化时，这一变化会沿反向路径影响其前驱状态。然而，并非所有受影响的“状态-动作”对都同等重要：价值变化幅度越大，其前驱状态就越可能需要大幅更新。

在随机环境中，更新的紧迫性还受到转移概率估计不确定性的影响。因此，应依据某种优先级度量（例如 TD 误差的绝对值）对更新任务进行排序。优先级遍历通过维护一个按优先级排序的队列，将计算资源集中于最可能引发价值显著变化的更新上，从而显著提升规划效率。

算法机制

对于任意“状态-动作”对 $(s,a)$，其优先级定义为：
$$P=\left|R+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })-Q(s,a)\right|,$$
其中 $(R,s^{\prime })=\text{Model}(s,a)$ 是由内部确定性模型给出的唯一转移结果。该优先级即为当前 TD 误差的绝对值，用于衡量此次更新可能引起的动作价值变化幅度。

每当一个 $(s,a)$ 被更新后，算法会找出所有能一步转移到 $s$ 的前驱状态-动作对 $(\bar{s},\bar{a})$（即满足 $\text{Model}(\bar{s},\bar{a})$ 的后继状态为 $s$ 的对）。对每个这样的前驱，重新计算其优先级 $P$；若 $P>\theta$（$\theta >0$ 为预设阈值），则将其以优先级 $P$ 插入优先队列。若某前驱已在队列中，则保留优先级更高的版本（实践中可通过允许重复插入或更新队列项实现，避免低效冗余更新）。

由于价值变化的影响在反向传播过程中随折扣因子 $\gamma$ 逐步衰减，其优先级通常会逐渐降低。当某状态-动作对的优先级降至阈值 $\theta$ 以下时，其更新对整体价值函数的影响可忽略，传播过程自然终止，从而避免无意义的计算。

算法实现

输入

• 状态集合 $\mathcal{S}$
• 动作集合 $\mathcal{A}(s)$（对每个 $s\in \mathcal{S}$）
• 策略函数 $policy(S,Q)$
• 学习率 $\alpha \in (0,1]$
• 折扣因子 $\gamma \in [0,1)$
• 优先级阈值 $\theta >0$
• 每次交互后的最大规划步数 $n$

初始化

• $\forall s\in \mathcal{S},a\in \mathcal{A}(s)$：
  • $Q(s,a)\leftarrow$ 任意初始值（如 0）
  • $Model(s,a)\leftarrow$ 未定义
• 优先队列 $PQueue\leftarrow \varnothing$

主循环（无限重复）

1. (a) $S\leftarrow$ 当前非终止状态

2. (b) $A\leftarrow policy(S,Q)$

3. © 执行 $A$，观测 $R$ 和 $S^{\prime }$

4. (d) 更新模型：
   $$Model(S,A)\leftarrow (R,S^{\prime })$$

5. (e) 计算优先级：
   $$P\leftarrow \left|R+\gamma \underset{a}{\max }Q(S^{\prime },a)-Q(S,A)\right|$$

6. (f) 若 $P>\theta$，将 $(S,A)$ 以优先级 $P$ 插入 $PQueue$

7. (g) 重复最多 $n$ 次，且当 $PQueue$ 非空时：

   • i. 取出并移除队首项：$(S,A)\leftarrow pop\_max(PQueue)$

   • ii. 获取模型预测：$(R,S^{\prime })\leftarrow Model(S,A)$

   • iii. 更新动作价值：
     $$Q(S,A)\leftarrow Q(S,A)+\alpha [R+\gamma \underset{a}{\max }Q(S^{\prime },a)-Q(S,A)]$$

   • iv. 对所有前驱 $(\bar{S},\bar{A})$ 满足 $Model(\bar{S},\bar{A})=(\bar{R},S)$：

     • 计算新优先级：
       $$P\leftarrow \left|\bar{R}+\gamma \underset{a}{\max }Q(S,a)-Q(\bar{S},\bar{A})\right|$$

     • 若 $P>\theta$，将 $(\bar{S},\bar{A})$ 以优先级 $P$ 插入 $PQueue$（若已存在则保留更高优先级）

实验

迷宫问题

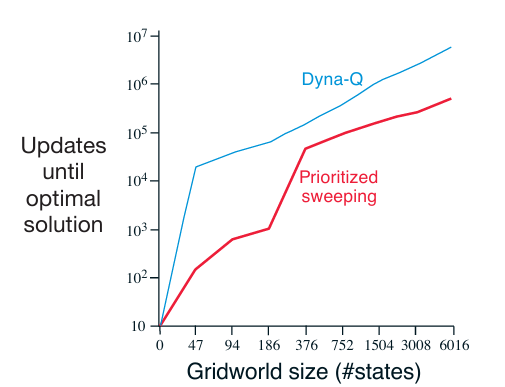
在标准迷宫任务中，优先级遍历相比无优先机制的 Dyna-Q，发现最优策略的速度通常快 5 至 10 倍。实验采用一系列结构相同但网格分辨率不同的迷宫环境。在每次与真实环境交互后，两个系统均执行最多 $n=5$ 次规划更新，其余条件（如学习率、探索策略、模型表示等）保持一致。在此公平比较下，优先级遍历始终展现出显著且稳定的性能优势。该结果验证了：反向聚焦机制与基于优先级的调度策略能够极大提升规划效率，尤其在稀疏奖励、长路径依赖的任务中效果尤为突出。

此外，优先级遍历可自然扩展至随机环境，关键在于对环境模型的表示方式与价值更新规则进行相应调整。具体而言，不再使用单次观测样本直接更新“状态-动作对”的价值，而是采用期望形式的更新，即综合考虑所有可能的后继状态及其转移概率：

$$Q(s,a)\leftarrow \sum _{s^{\prime },r}\hat{\mathcal{P}}(s^{\prime },r\mid s,a)\left[r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })\right],$$

其中 $\hat{\mathcal{P}}(s^{\prime },r\mid s,a)$ 是基于经验估计的转移-奖励联合分布。相应地，优先级也应反映模型更新或价值变化所引起的期望 TD 误差变化量，从而维持高效规划的核心思想。

杆子操控问题

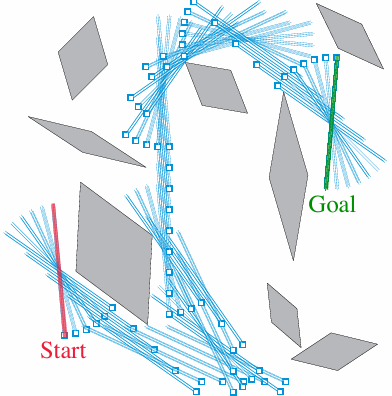
该任务的目标是在一个有限矩形工作空间中，以最少步数将一根杆子从起始位姿移动到目标位姿，同时避开静态障碍物。环境是确定性的，但具有复杂的几何约束。

智能体可执行以下四种离散动作：

• 沿杆子长轴方向平移；
• 沿垂直于长轴方向平移；
• 绕杆子中心顺时针旋转 $10^{\circ }$；
• 绕杆子中心逆时针旋转 $10^{\circ }$。

其中，每次平移的距离约为工作空间边长的 $1/20$，旋转增量固定为 $10^{\circ }$。

状态表示

• 位置：离散化为 $20\times 20$ 的网格；

• 朝向：离散为 $360^{\circ }/10^{\circ }=36$ 个方向；

• 总状态数：
  $$20\times 20\times 36=14,400.$$

部分状态因与障碍物发生几何重叠而被标记为无效状态（不可达）。

算法运行后成功，隐式构建了障碍物地图（通过模型记录导致碰撞的无效转移）；找到了从起点到目标的最短可行路径（即最优位姿序列）。结果可视化清晰展示了障碍物的空间分布与规划出的无碰撞路径。

该问题对非优先规划方法（如标准 Dyna-Q）极具挑战性，因为状态空间规模大（$>10^4$）且奖励极度稀疏（仅在目标状态获得正回报）。在均匀采样的 Dyna-Q 中，价值信息从目标状态向外传播极其缓慢，绝大多数模拟更新发生在远离价值传播前沿（information frontier）的区域，TD 误差接近零，无实质影响。在合理计算预算内，价值信号难以反向传播至起始状态。因此，该问题可能已大到无法用非优先遍历的方法有效解决。

总结

优先遍历在随机环境中使用期望更新，可能浪费计算资源在低概率转移上，引入大量冗余计算。下文中的采样方法和小范围回溯将解决这个问题。