第8章 基于表格型方法的规划和学习(2) Dyna-Q+：基于时间的探索奖励

当模型错误的时候

在上一节的迷宫示例中，模型从空开始，仅填充完全正确的信息，同时模型的变化是相对有限的。然而在一般情况下，模型可能不正确，原因包括在随机环境中仅观察到有限样本；模型由泛化能力较差的函数近似；环境发生变化，而新的动态尚未被观测。当模型错误时，规划过程可能计算出次优策略。

乐观模型有助于快速发现错误

若模型乐观（即预测比实际更高的收益或更优的状态转移），规划会驱使智能体尝试这些虚假机会。智能体很快会发现这些机会不存在，从而感知并修正模型错误。

屏障迷宫案例

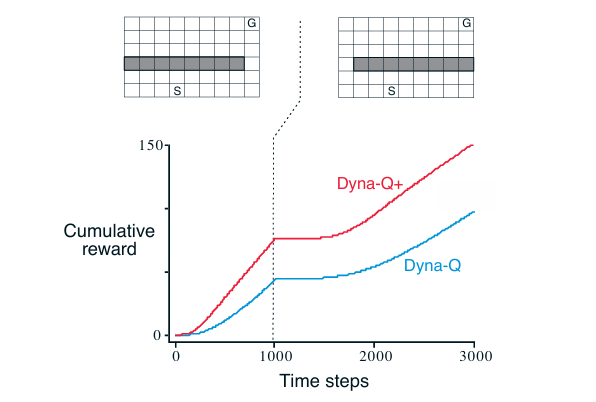
初始环境下最短路径从屏障右侧绕行。 1000 步后环境发生变化，原路径被封锁，新最短路径从左侧绕行。

[!NOTE]

横轴智能体与环境交互的总步数（真实交互步数）。

纵轴累计回报（注意：此处是“累计”，不是“平均”）。

假设每成功到达目标（G）获得 +1 奖励；其他步骤奖励为 0；一幕从起点 S 开始，到 G 结束。

那么累计回报 = 成功次数 × 1（因为每次成功得 +1）；累计回报的增长速率 = 单位时间内成功的次数。

**初期（0–300 步）**策略随机 → 很少成功 → 累计回报增长缓慢（曲线平缓）；**中期（300–800 步）**通过规划和学习 → 找到较优路径 → 成功频率上升 → 累计回报加速增长（曲线变陡）；后期（800–1000 步）策略基本收敛 → 成功频率稳定 → 累计回报以恒定斜率线性增长（即“直线增长”）。因此，“直线增长”表示：智能体已学会最优策略，每幕耗时稳定，单位时间成功次数恒定 → 累计回报随时间线性增加。累计回报进入稳定线性增长阶段，意味着策略已优化至最优水平。

第 1000 步后曲线变平主要是因为环境突变，原最短路径被封锁 → 旧策略失效；智能体仍按旧模型规划 → 尝试走已被堵死的路径 → 无法到达目标；因此不再获得 +1 奖励 → 累计回报停止增长 → 曲线变平。此时累计回报并未下降，只是增长停滞，说明性能暂时退化。

后期Dyna-Q依赖真实交互逐步发现新路径 → 最终恢复增长，但较慢；**Dyna-Q+**因引入“探索奖励”（对长期未尝试的状态-动作给予额外收益）→ 主动试探右侧新路径 → 更快发现新最优路径 → 累计回报更快恢复线性增长。

Dyna-Q+ 在 Dyna-Q 基础上引入额外试探收益，鼓励探索。Dyna-Q 与 Dyna-Q+ 均在前 1000 步内找到最优路径。环境变化后，两者性能暂时下降（曲线变平，智能体在屏障后徘徊，没有得到收益)；但随后均能学习新最优策略。

悲观或静态模型难以发现环境改善

当环境变得更好（如出现新捷径），但原有策略未反映此改善时，智能体可能长期无法发现变化，因为其模型未更新，规划持续依赖错误信息。

捷径迷宫案例

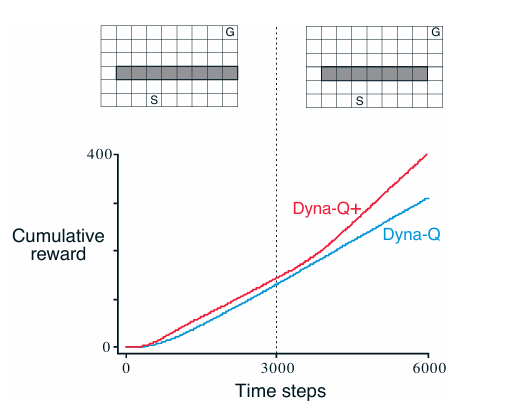
此时初始环境最优路径绕屏障左侧。 3000 步后右侧开启更短路径，原路径仍可用。但是Dyna-Q 从未发现新捷径，其模型认为右侧无通路，规划越频繁，越不会尝试右侧动作。即使使用 $\epsilon$-greedy 策略，试探概率也难以积累足够探索以发现捷径。

试探与开发的矛盾

试探意味着执行动作以改进模型（发现环境变化）； 开发则意味着基于当前模型执行最优动作。我们的目标是在不显著降低平均性能的前提下，有效发现环境变化。 虽无完美解法，但简单启发式方法常有效。

Dyna-Q+ 的启发式试探机制

Dyna-Q+ 引入计算上的好奇心，对每个状态-动作对 $(s,a)$，记录自上次真实交互以来经过的时间 $\tau (s,a)$。若某转移在 $\tau$ 步内未被尝试，则在模拟经验中为其赋予额外收益：
$$r_{\text{modified}}=r+\kappa \sqrt{\tau }$$
其中 $\kappa >0$ 为小常数。该机制鼓励智能体周期性试探长期未访问的状态转移，即使需执行一长串动作。虽有试探成本，但在如捷径迷宫等场景中，收益远大于代价。

练习

为何 Dyna-Q+ 在“屏障迷宫”和“捷径迷宫”的两个阶段均优于 Dyna-Q？

Dyna-Q+ 在“屏障迷宫”（环境变差：原路径被封锁）和“捷径迷宫”（环境变好：新捷径出现）两个场景中均优于 Dyna-Q，其根本原因在于 Dyna-Q+ 引入了基于时间的探索激励机制（即“计算好奇心”），使其能更主动、持续地探测长期未访问的状态-动作对，从而更快适应环境的非平稳变化。

在“屏障迷宫”中（环境恶化）第 1000 步后，原最优路径被封锁，智能体若继续依赖旧模型，将反复尝试无效动作，无法到达目标。Dyna-Q 的局限在于仅依靠 ε-greedy 进行随机探索，试探强度弱且无方向性；在高维或长路径任务中，偶然试探难以触发对新可行路径的完整发现。Dyna-Q+ 的优势在于对长期未执行的状态-动作对（如左侧绕行的动作序列）赋予额外奖励。即使这些动作在旧模型中被认为“无用”，其模拟规划也会因探索奖励而被优先考虑。因此，Dyna-Q+ 能主动重新探索被忽视的区域，更快发现左侧新路径，恢复性能。

在“捷径迷宫”中（环境改善）第 3000 步后右侧出现更短路径，但 Dyna-Q 的模型仍认为右侧不可达（因从未成功穿越），规划始终避开该区域。Dyna-Q 的困境在于模型未更新 → 规划结果持续强化旧策略。ε-greedy 的随机试探概率低，且单次试探不足以完成整条新路径，无法获得正反馈，导致探索无法积累。结果是陷入“模型盲区”，长期无法发现捷径。Dyna-Q+ 的优势在于右侧状态-动作对因长期未被真实执行，其 $\tau (s,a)$ 持续增长，模拟中的探索奖励也随之增大。规划过程会主动构造包含这些高探索奖励动作的轨迹，驱使智能体在真实环境中尝试右侧路径。一旦成功穿越，立即获得 +1 奖励，模型迅速更新，策略快速切换至新最优路径。

Dyna-Q+ 的核心创新在于将探索动机内化到规划过程中不依赖外部随机性（如 ε-greedy）进行低效试探；而是通过时间驱动的内在奖励，系统性地“怀疑”长期未验证的模型假设；这使其既能应对环境恶化（需放弃旧策略），也能抓住环境改善（需发现新机会）。相比之下，Dyna-Q 的模型一旦收敛，就缺乏主动验证其有效性的机制，在动态环境中表现出模型固化。

捷径迷宫案例中，Dyna-Q+ 与 Dyna-Q 的性能差距在第一阶段为何略有收窄？

在第一阶段，环境是静态且已收敛的,最优策略已找到（例如绕左侧路径）；所有状态-动作对中，只有最优路径上的动作能高效到达目标；其他动作（如尝试右侧）在真实环境中无效或低效。然而，Dyna-Q+ 仍会为长期未执行的动作（如右侧探索动作）赋予额外的探索奖励 。这导致规划过程中生成包含非最优动作的模拟轨迹；策略偶尔被“诱惑”去执行这些高探索奖励但实际无效的动作；真实交互中浪费步数尝试无用路径，降低单位时间的成功率；因此，累计回报的增长速率略低于纯开发导向的 Dyna-Q。Dyna-Q+ 为未来的环境变化“预付”了探索成本，牺牲了静态环境下的部分性能。