热身题
Exercise 1
题目:所有的马都有同样的颜色,我们可以对给定集合中的马匹数量运用归纳法来证明之。理由就是:“如果恰有一匹马,那么它与它自身有相同的颜色,故而基础是显然的。根据归纳法的步骤,假设有 nnn 匹马,标号从 1 到 nnn。根据归纳假设,标号从 1 到 n−1n-1n−1 的马都有同样的颜色;类似地,标号从 2 到 nnn 的马也有同样的颜色。但是,处于中间位置标号从 2 到 n−1n-1n−1 的马,当它们在不同的马群中时不可能改变颜色,因为这些是马,而不是变色龙。故而依据传递性可知,标号从 1 到 nnn 的马也必定有同样的颜色,于是全部 nnn 匹马都有同样的颜色。证毕。”如果这一推理有误,那么错在哪儿?
分析:归纳法结构回顾
数学归纳法的标准形式如下:
- 基础情况:验证命题对 n=1n = 1n=1 成立。
- 归纳假设:假设命题对某个 n=k≥1n = k \geq 1n=k≥1 成立。
- 归纳步骤:证明命题对 n=k+1n = k+1n=k+1 成立。
在本题中,目标是证明:对任意正整数 nnn,任意 nnn 匹马的颜色都相同。
- 基础情况:n=1n = 1n=1,单匹马颜色“相同”是平凡成立的。
- 归纳假设:任意 nnn 匹马颜色相同。
- 归纳步骤:考虑 n+1n+1n+1 匹马,编号为 1,2,…,n+11, 2, \dots, n+11,2,…,n+1。
构造两个子集:
- 集合 A={1,2,…,n}A = \{1, 2, \dots, n\}A={1,2,…,n}:前 nnn 匹马;
- 集合 B={2,3,…,n+1}B = \{2, 3, \dots, n+1\}B={2,3,…,n+1}:后 nnn 匹马。
注意:
- ∣A∣=n|A| = n∣A∣=n,∣B∣=n|B| = n∣B∣=n,且 A∪B={1,2,…,n+1}A \cup B = \{1, 2, \dots, n+1\}A∪B={1,2,…,n+1},即全部 n+1n+1n+1 匹马。
- 交集为 A∩B={2,3,…,n}A \cap B = \{2, 3, \dots, n\}A∩B={2,3,…,n},即中间的 n−1n-1n−1 匹马。
由归纳假设:
- AAA 中所有马颜色相同;
- BBB 中所有马颜色相同。
若 A∩BA \cap BA∩B 非空,则存在共同马匹,其颜色在 AAA 和 BBB 中一致,从而可推出 A∪BA \cup BA∪B 中所有马颜色相同。
关键问题:交集是否非空?
交集 A∩B={2,3,…,n}A \cap B = \{2, 3, \dots, n\}A∩B={2,3,…,n} 非空 当且仅当 n≥2n \geq 2n≥2。
但当 n=1n = 1n=1 时(即从 n=1n=1n=1 推 n=2n=2n=2):
- A={1}A = \{1\}A={1}
- B={2}B = \{2\}B={2}
- A∩B=∅A \cap B = \emptysetA∩B=∅
此时两个子集无公共马匹,无法建立颜色之间的联系。因此,尽管 AAA 内颜色一致、BBB 内颜色一致,但无法推出第 1 匹和第 2 匹马颜色相同。
错误定位
该归纳法的归纳步骤在 n=1→n=2n=1 \to n=2n=1→n=2 时不成立,因为两个大小为 n=1n=1n=1 的子集没有交集,无法传递颜色信息。
虽然归纳假设在 n=1n=1n=1 成立,但无法用于推导 n=2n=2n=2 的情况。整个归纳链条在此断裂。
结论
该证明的逻辑漏洞在于:归纳步骤依赖于两个子集的非空交集,而这一条件在 n=1n=1n=1 时失效。因此,不能从 n=1n=1n=1 推出 n=2n=2n=2,归纳法失败。
最终答案:推理的错误在于归纳步骤在 n=1n=1n=1 到 n=2n=2n=2 时不成立。当 n=1n=1n=1 时,两个子集 $ {1} $ 和 $ {2} $ 没有共同元素,无法通过交集传递颜色。整个归纳链在此处断裂,导致证明无效。
Exercise 2
题目:把有 nnn 个圆盘的塔从左边的桩柱 A 移动到右边的桩柱 B,不允许在 A 和 B 之间直接移动。每一次移动都必须是移动到中间的桩柱 C 或从中间的桩柱 C 移出。较大的圆盘永远不能放在较小圆盘的上面。求最短的移动序列。
问题分析
与经典汉诺塔问题不同,本题增加了限制:不允许在 A 和 B 之间直接移动。所有移动必须经过中间桩柱 C。即:
- 只允许的移动类型:
A↔CA \leftrightarrow CA↔C,C↔BC \leftrightarrow BC↔B - 禁止的移动类型:
A↔BA \leftrightarrow BA↔B,B↔AB \leftrightarrow AB↔A
目标:将 nnn 个圆盘从 A 移动到 B,遵守大小顺序限制。
递推关系建立
设 XnX_nXn 为将 nnn 个圆盘从 A 经由 C 移动到 B 所需的最少移动次数。
考虑递归结构:
-
步骤 1:将上面 n−1n-1n−1 个圆盘从 A 移动到 B(作为临时存放),但必须经过 C,且不能直接 A→B。
这相当于递归地将 n−1n-1n−1 个盘从 A → B,使用 C 作为辅助。所需次数:Xn−1X_{n-1}Xn−1 -
步骤 2:将最大的圆盘从 A → C(唯一合法路径中转)。
次数:1 -
步骤 3:将 n−1n-1n−1 个圆盘从 B 移回 A(以便腾出 B 接收最大盘),使用 C 为中介。
相当于从 B → A,递归过程,次数:Xn−1X_{n-1}Xn−1 -
步骤 4:将最大圆盘从 C → B。
次数:1 -
步骤 5:将 n−1n-1n−1 个圆盘从 A 移动到 B,完成最终堆叠。
次数:Xn−1X_{n-1}Xn−1
总移动次数
Xn=Xn−1+1+Xn−1+1+Xn−1=3Xn−1+2 X_n = X_{n-1} + 1 + X_{n-1} + 1 + X_{n-1} = 3X_{n-1} + 2 Xn=Xn−1+1+Xn−1+1+Xn−1=3Xn−1+2
初始条件:
X0=0
X_0 = 0
X0=0
求解递推式
我们有:
Xn=3Xn−1+2,X0=0
X_n = 3X_{n-1} + 2,\quad X_0 = 0
Xn=3Xn−1+2,X0=0
使用“加1法”简化:
令 Yn=Xn+1Y_n = X_n + 1Yn=Xn+1,则:
Yn=Xn+1=3Xn−1+2+1=3(Xn−1+1)=3Yn−1
Y_n = X_n + 1 = 3X_{n-1} + 2 + 1 = 3(X_{n-1} + 1) = 3Y_{n-1}
Yn=Xn+1=3Xn−1+2+1=3(Xn−1+1)=3Yn−1
初始值:Y0=X0+1=1Y_0 = X_0 + 1 = 1Y0=X0+1=1
因此:
Yn=3n⇒Xn=3n−1
Y_n = 3^n \quad \Rightarrow \quad X_n = 3^n - 1
Yn=3n⇒Xn=3n−1
结论
最短移动次数为:
Xn=3n−1
X_n = 3^n - 1
Xn=3n−1
此外,在移动 12Xn=3n−12\frac{1}{2}X_n = \frac{3^n - 1}{2}21Xn=23n−1 次后,整个塔将位于中间桩柱 C 上,正好完成前半段(A → C),此时距离最终目标(A → B)还有一半的路程(从移动次数角度看,后半段也需 Xn−1+1+Xn−1+1+Xn−1X_{n-1} + 1 + X_{n-1} + 1 + X_{n-1}Xn−1+1+Xn−1+1+Xn−1,但对称性使得中间点确为 CCC 上的完整塔)。
最终答案:最短移动次数为 Xn=3n−1X_n = 3^n - 1Xn=3n−1。
Exercise 3
题目:证明,在 Exercise 2 的限制下(即不允许在 A 和 B 之间直接移动,所有移动必须经过中间柱 C),将 nnn 个圆盘从桩柱 A 移动到桩柱 B 的最短移动过程中,我们会在三根桩柱上都遇到 nnn 个圆盘的每一种正确的叠放方式。
解题思路
本题要求证明:在受限汉诺塔问题的最优移动序列中,每一个满足堆叠规则(大盘不压小盘)的圆盘分布状态都会被恰好访问一次。
我们将从以下几个方面逐步展开证明:
- 明确“正确叠放”的含义
- 回顾移动规则与总步数
- 分析状态空间的大小
- 证明移动路径遍历所有合法状态
- 结论
1. 什么是“正确的叠放”
一个“正确的叠放”是指:
- 每个圆盘被分配到三根桩柱 A、B 或 C 中的一根;
- 在每一根桩柱上,圆盘按照大小自底向上递减排列(即大盘在下,小盘在上);
- 圆盘之间不重叠,且满足汉诺塔规则。
关键点:每一个将 nnn 个圆盘分配到三根柱子的方案(共 3n3^n3n 种),都唯一确定一个合法的叠放状态。
这是因为:对于任意一种分配方式,我们只需在每根柱子上将属于它的圆盘按编号从大到小(从底到顶)排列,即可得到一个合法状态。
例如:
- 若圆盘 1(最小)在 A,圆盘 2 在 B,圆盘 3(最大)在 A,
- 则 A 柱上有圆盘 3(底)、1(顶),B 柱有圆盘 2,C 柱为空 → 合法。
因此,不存在“非法的分配”,因为堆叠顺序是由分配自动决定的(按大小排序)。
换言之:所有 3n3^n3n 种分配方式,都一一对应一个合法的叠放状态。
所以,合法状态总数为:
∣Sn∣=3n
|\mathcal{S}_n| = 3^n
∣Sn∣=3n
2. 移动规则与最短移动次数回顾(Exercise 2)
- 不允许 A ↔ B 直接移动;
- 所有移动必须经过中间柱 C;
- 大盘不能放在小盘上。
设 XnX_nXn 为将 nnn 个圆盘从 A 移动到 B 所需的最少移动次数。
递推关系:
Xn=3Xn−1+2,X0=0
X_n = 3X_{n-1} + 2, \quad X_0 = 0
Xn=3Xn−1+2,X0=0
解得:
Xn=3n−1
X_n = 3^n - 1
Xn=3n−1
这意味着:整个移动过程包含 3n−13^n - 13n−1 次移动,共经历 3n3^n3n 个状态(初始状态 + 每一步之后的状态)。
3. 状态转移特性
- 每次移动只改变一个圆盘的位置(从一根柱子到另一根);
- 因此,状态编码中只有一位发生变化;
- 所有中间状态均满足堆叠规则(由移动规则保证);
- 状态总数为 3n3^n3n,而移动序列共访问 3n3^n3n 个状态。
4. 证明:所有合法状态都被访问
我们已知:
- 合法状态总数:3n3^n3n
- 移动过程经历的状态数:3n3^n3n(从开始到结束共 3n−13^n - 13n−1 步)
- 所有状态均为合法(由规则保证)
- 若这些状态互不相同,则必覆盖所有合法状态
证明无重复状态:
假设某个状态在移动过程中重复出现。由于整个移动序列是确定性的(最优递归策略固定),一旦状态重复,系统将进入循环,无法在有限步内到达目标状态。
但已知 Xn=3n−1X_n = 3^n - 1Xn=3n−1 是有限且正确的最小步数,矛盾。
因此,所有 3n3^n3n 个状态互不相同。
进而,该移动序列访问了所有 3n3^n3n 个合法状态,每一种正确的叠放方式都被恰好经历一次。
5. 与三进制格雷码的类比(补充说明)
我们可以将每个状态编码为一个 nnn 位三进制数 (d1,d2,…,dn)(d_1, d_2, \dots, d_n)(d1,d2,…,dn),其中:
- di=0,1,2d_i = 0, 1, 2di=0,1,2 分别表示第 iii 个圆盘(从小到大编号)位于 A、C、B;
- 每次移动只改变一个圆盘的位置 → 编码中只有一位发生变化。
整个移动序列从 (0,0,…,0)(0,0,\dots,0)(0,0,…,0)(所有盘在 A)到 (2,2,…,2)(2,2,\dots,2)(2,2,…,2)(所有盘在 B),遍历所有 3n3^n3n 个三进制组合,每次只改变一位。
这正是三进制格雷码(Ternary Gray Code) 的结构特征。
因此,该过程在状态空间中形成了一条哈密顿路径(Hamiltonian path)——访问每个节点恰好一次。
最终答案:在 Exercise 2 的限制下,将 nnn 个圆盘从 A 移动到 B 的最短移动过程共经历 3n3^n3n 个不同的状态。由于所有满足堆叠规则的合法叠放方式恰好有 3n3^n3n 种,且移动过程中状态不重复、始终保持合法,因此该过程遍历了每一种正确的叠放方式。故在移动过程中,我们会在三根桩柱上都遇到 nnn 个圆盘的每一种正确的叠放。
Exercise 4
题目:是否存在 nnn 个圆盘在 3 根桩柱上的某种开始叠放或结束叠放,使得按照卢卡斯原来的规则(即经典汉诺塔规则:每次移动一个圆盘,大盘不能放在小盘上),需要多于 2n−12^n - 12n−1 次的移动?
问题分析
经典汉诺塔问题中,将 nnn 个圆盘从一根桩柱全部移动到另一根桩柱所需的最少移动次数为:
2n−1
2^n - 1
2n−1
这是在“所有圆盘初始在一根柱上,目标为全部移到另一根柱”的前提下得出的最小步数。
本题问的是:是否存在某种初始叠放和目标叠放(不要求全在一根柱上),使得从该初始状态到目标状态所需的最少移动步数超过 2n−12^n - 12n−1?
换句话说:是否存在一对合法状态(起始和终止),它们之间的最短移动路径长度 > 2n−12^n - 12n−1?
状态空间与最大距离
- 合法状态总数:3n3^n3n(每个圆盘可在 A、B、C 之一,每根柱上按大小顺序堆叠)
- 经典汉诺塔的完整移动(如 A → B)需要 2n−12^n - 12n−1 步
- 但这是特定路径的长度
我们考虑状态图:
- 每个节点是一个合法状态(共 3n3^n3n 个)
- 每条边表示一次合法移动(移动一个圆盘到另一根柱,且不违反大小规则)
- 任意两状态之间的最短路径长度为它们之间的“移动距离”
问题转化为:
在这个图中,是否存在两个状态,其最短路径长度 > 2n−12^n - 12n−1?
关键观察:任何状态到另一个状态的移动步数不会超过 2n−12^n - 12n−1
我们证明更强的结论:
对于任意初始状态和任意目标状态,都存在一条长度不超过 2n−12^n - 12n−1 的移动序列将其连接。
我们用归纳法证明:
归纳假设:对 k<nk < nk<n,任意 kkk 个圆盘的任意起始和目标状态之间,可以在至多 2k−12^k - 12k−1 步内完成移动。
归纳步骤(对 nnn 个圆盘):
考虑最大圆盘(编号 nnn)的位置:
情况 1:最大圆盘在起始状态和目标状态中位于同一根柱子上,且其下方无其他圆盘(即它在该柱最底)。
- 此时我们不需要移动最大圆盘。
- 只需将其余 n−1n-1n−1 个圆盘从当前位置调整到目标位置(可能分布在三根柱上)。
- 由归纳假设,调整 n−1n-1n−1 个圆盘最多需要 2n−1−12^{n-1} - 12n−1−1 步。
- 由于最大圆盘不动,其余圆盘可在其所在柱的“上方空间”外自由移动(即使用另外两根柱作为辅助)。
- 因此,总步数 ≤ 2n−1−1<2n−12^{n-1} - 1 < 2^n - 12n−1−1<2n−1
情况 2:最大圆盘在起始和目标状态中位于不同柱子上。
则必须移动最大圆盘一次(从原柱到目标柱)。
步骤如下:
- 将除最大圆盘外的 n−1n-1n−1 个圆盘从当前状态移动到第三根柱(既非最大盘起始柱,也非目标柱),作为临时存放;
- 由归纳假设,最多需 2n−1−12^{n-1} - 12n−1−1 步;
- 将最大圆盘从起始柱移动到目标柱;
- 1 步;
- 将 n−1n-1n−1 个圆盘从临时柱移动到目标柱,按目标状态重新排列;
- 最多需 2n−1−12^{n-1} - 12n−1−1 步。
总步数 ≤:
(2n−1−1)+1+(2n−1−1)=2n−1
(2^{n-1} - 1) + 1 + (2^{n-1} - 1) = 2^n - 1
(2n−1−1)+1+(2n−1−1)=2n−1
因此,在任何情况下,移动步数都不超过 2n−12^n - 12n−1。
结论
- 无论初始和目标状态如何,所需最少移动步数 不会超过 2n−12^n - 12n−1;
- 经典汉诺塔的 2n−12^n - 12n−1 步是最大可能的最短路径长度;
- 当且仅当需要移动最大圆盘,且递归结构完整时,达到该上界。
最终答案:不存在这样的初始和目标叠放方式。对于 nnn 个圆盘在三根桩柱上的任意合法起始状态和目标状态,按照卢卡斯规则,总存在一个移动序列,其长度不超过 2n−12^n - 12n−1。因此,不可能需要多于 2n−12^n - 12n−1 次移动。
Exercise 5
题目:由3个重叠的圆做成的维恩图常用来描述与3个给定集合有关的8个可能的子集。由4个给定集合给出的16种可能的子集能否用4个重叠的圆来描述?
问题分析
维恩图(Venn diagram)要求表示 nnn 个集合之间所有可能的交集关系,即要清晰地展示出 2n2^n2n 个不同的区域,每个区域对应一个子集:元素属于或不属于每一个集合。
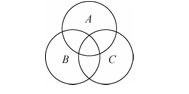
- 当 n=3n = 3n=3 时,23=82^3 = 823=8 个区域,可以用三个相互重叠的圆实现;
- 本题问:是否可以用 四个圆 构造一个维恩图,表示 24=162^4 = 1624=16 个区域?
关键限制:圆的几何性质
两个圆在平面上最多有两个交点(除非重合,但重合无法增加新区域)。
我们考虑:在已有 n−1n-1n−1 个圆的基础上,加入第 nnn 个圆,最多能新增多少个区域?
- 一个新圆若与已有每个圆最多交于 2 点,则与 kkk 个已有圆最多有 2k2k2k 个交点;
- 这些交点将新圆分割成最多 2k2k2k 段弧;
- 每一段弧最多穿过一个已有区域,并将其一分为二,从而新增一个区域;
- 因此,第 nnn 个圆最多新增 2k2k2k 个区域。
递推:最多能生成多少个区域
设 R(n)R(n)R(n) 为 nnn 个圆在平面上最多能划分出的区域数。
已知:
- R(0)=1R(0) = 1R(0)=1
- 每个新圆最多新增 2×(已有的圆数)2 \times (已有的圆数)2×(已有的圆数) 个区域
计算:
- R(1)=R(0)+2×0=1+1=2R(1) = R(0) + 2 \times 0 = 1 + 1 = 2R(1)=R(0)+2×0=1+1=2(一个圆分平面为内、外)
- R(2)=R(1)+2×1=2+2=4R(2) = R(1) + 2 \times 1 = 2 + 2 = 4R(2)=R(1)+2×1=2+2=4
- R(3)=R(2)+2×2=4+4=8R(3) = R(2) + 2 \times 2 = 4 + 4 = 8R(3)=R(2)+2×2=4+4=8
- R(4)=R(3)+2×3=8+6=14R(4) = R(3) + 2 \times 3 = 8 + 6 = 14R(4)=R(3)+2×3=8+6=14
因此,四个圆最多只能划分出 14 个区域。
但 24=162^4 = 1624=16,我们需要 16 个区域 来表示 4 个集合的所有子集组合。
由于 14<1614 < 1614<16,不可能用四个圆构造出包含所有 16 个区域的维恩图。
补充说明:使用其他形状是可能的
虽然圆做不到,但若使用更灵活的闭合曲线(如卵形、椭圆),可以增加交点数量:
- 两个椭圆最多可有 4 个交点;
- 这使得第四个椭圆可以与前三个产生更多交点,从而分割出更多区域;
- 实际上,已知存在由 4 个卵形 构成的维恩图,能表示全部 16 个区域。
进一步地:
- 维恩本人曾认为无法用椭圆表示 5 个集合(25=322^5 = 3225=32 区域);
- 但 Grünbaum 发现了一种用 5 个椭圆 构造的维恩图,成功表示所有 32 个区域。
这说明:曲线的交点能力比凸性更重要。决定能否构造维恩图的关键是 每对曲线之间的最大交点数,而非是否为圆或椭圆。
最终答案:不能。四个圆最多只能划分出 14 个区域,而 4 个集合需要表示 24=162^4 = 1624=16 种子集组合,因此无法用四个圆构造出完整的维恩图。然而,使用卵形或其他闭合曲线是可能的,因为它们可以产生更多交点。事实表明,交点的个数决定了区域的最大数量,而凸性只是一个次要因素。
Exercise 6
题目:平面上由 nnn 条直线定义的某些区域是无界的,而另一些区域则是有界的。有界区域的最大个数是多少?
问题分析
给定平面上 nnn 条直线,它们将平面划分为若干区域。这些区域中:
- 一些是无界区域(延伸到无穷远);
- 一些是有界区域(完全封闭的多边形区域)。
本题要求:在所有可能的 nnn 条直线的构型中,有界区域的最大个数是多少?
前提:最大化区域划分的条件
为了使总的区域数和有界区域数尽可能多,我们假设:
- 任意两条直线不平行(否则交点减少);
- 任意三条直线不共点(即无三线共点);
- 每对直线恰有一个交点。
这样的构型称为处于一般位置(in general position)的直线。
总区域数
设 LnL_nLn 为 nnn 条直线在一般位置下划分平面的总区域数。已知递推关系:
Ln=Ln−1+n,L0=1 L_n = L_{n-1} + n, \quad L_0 = 1 Ln=Ln−1+n,L0=1
解得:
Ln=n(n+1)2+1
L_n = \frac{n(n+1)}{2} + 1
Ln=2n(n+1)+1
有界区域的来源
有界区域是被完全包围的多边形区域,例如三角形、四边形等。
关键观察:
- 一条新加入的直线,若与已有 n−1n-1n−1 条直线交于 n−1n-1n−1 个不同点(即处于一般位置),则被这些交点分割为 nnn 段(n−1n-1n−1 个有限段 + 2 个无限射线);
- 其中,中间的 n−1n-1n−1 个交点将新直线分为 nnn 部分:2 个无限部分(两端)和 n−2n-2n−2 个有限线段;
- 每一段穿过一个已有区域,将其一分为二;
- 因此,第 nnn 条直线新增 nnn 个区域。
但这些新增区域中,哪些是有界的?
新增有界区域的数量
当加入第 nnn 条直线时:
- 它与前 n−1n-1n−1 条直线交于 n−1n-1n−1 个点;
- 这些点将其分为 nnn 段;
- 其中,中间的 n−2n-2n−2 段是有限线段,位于两个交点之间;
- 每一段穿过一个已有区域,若该段被包围,则可能形成新的有界区域。
但更精确的结论是:
当第 nnn 条直线与前 n−1n-1n−1 条直线交于 n−1n-1n−1 个不同点(且无三线共点),它会新增 n−2n - 2n−2 个有界区域。
解释:
- 新增的有界区域来自于新直线穿过的“内部”区域;
- 在一般位置下,第 nnn 条直线会穿过 nnn 个已有区域;
- 其中,两端的两个区域是无界的,被分割后仍保留无界部分;
- 中间的 n−2n - 2n−2 个区域可能是有界的,且每穿过一个,就可能“封闭”出一个新的有界区域;
- 实际上,可以证明:新增的有界区域数为 n−2n - 2n−2(当 n≥2n \geq 2n≥2,否则为 0)。
递推计算有界区域总数
设 BnB_nBn 为 nnn 条直线在一般位置下的有界区域最大个数。
初始:
- B0=0B_0 = 0B0=0
- B1=0B_1 = 0B1=0(一条直线不分割出有界区域)
- B2=0B_2 = 0B2=0(两条直线交于一点,形成四个无界区域)
递推关系:
Bn=Bn−1+(n−2),for n≥2
B_n = B_{n-1} + (n - 2), \quad \text{for } n \geq 2
Bn=Bn−1+(n−2),for n≥2
展开:
Bn=(n−2)+(n−3)+⋯+1+0+0=∑k=1n−2k=(n−2)(n−1)2
\begin{align*}
B_n &= (n-2) + (n-3) + \cdots + 1 + 0 + 0 \\
&= \sum_{k=1}^{n-2} k = \frac{(n-2)(n-1)}{2}
\end{align*}
Bn=(n−2)+(n−3)+⋯+1+0+0=k=1∑n−2k=2(n−2)(n−1)
结论
有界区域的最大个数为:
Bn=(n−1)(n−2)2
B_n = \frac{(n-1)(n-2)}{2}
Bn=2(n−1)(n−2)
验证小值
- n=0n = 0n=0: B0=0B_0 = 0B0=0
- n=1n = 1n=1: B1=0B_1 = 0B1=0
- n=2n = 2n=2: B2=0=1⋅02B_2 = 0 = \frac{1 \cdot 0}{2}B2=0=21⋅0
- n=3n = 3n=3: 三条直线构成一个三角形(唯一有界区域):B3=1=2⋅12B_3 = 1 = \frac{2 \cdot 1}{2}B3=1=22⋅1
- n=4n = 4n=4: B4=3⋅22=3B_4 = \frac{3 \cdot 2}{2} = 3B4=23⋅2=3,实际中四条线可形成三个有界三角形或四边形
符合。
最终答案:有界区域的最大个数是 (n−1)(n−2)2\frac{(n-1)(n-2)}{2}2(n−1)(n−2)。
Exercise 7
题目:设H(n)=J(n+1)−J(n)H(n) = J(n+1) - J(n)H(n)=J(n+1)−J(n)。已知有递推关系(参考方程 (1.8)):
- H(2n)=2H(2n) = 2H(2n)=2
- 对n≥1n \geq 1n≥1,有
H(2n+1)=J(2n+2)−J(2n+1)=(2J(n+1)−1)−(2J(n)+1)=2H(n)−2 H(2n+1) = J(2n+2) - J(2n+1) = (2J(n+1) - 1) - (2J(n) + 1) = 2H(n) - 2 H(2n+1)=J(2n+2)−J(2n+1)=(2J(n+1)−1)−(2J(n)+1)=2H(n)−2
于是,有人认为可以通过对nnn使用归纳法,证明对所有nnn都有H(n)=2H(n) = 2H(n)=2。问:这个推理错在哪里?
背景回顾:约瑟夫斯函数J(n)J(n)J(n)
J(n)J(n)J(n)是经典约瑟夫斯问题的解,表示在nnn个人围成一圈、每数到第2个人就淘汰的规则下,最后幸存者的初始位置(从1开始编号)。其递推关系为:
J(1)=1J(2n)=2J(n)−1J(2n+1)=2J(n)+1 \begin{aligned} J(1) &= 1 \\ J(2n) &= 2J(n) - 1 \\ J(2n+1) &= 2J(n) + 1 \end{aligned} J(1)J(2n)J(2n+1)=1=2J(n)−1=2J(n)+1
定义函数H(n)=J(n+1)−J(n)H(n) = J(n+1) - J(n)H(n)=J(n+1)−J(n)
我们分析H(n)H(n)H(n)的行为。
根据题设:
-
H(2n)=J(2n+1)−J(2n)H(2n) = J(2n+1) - J(2n)H(2n)=J(2n+1)−J(2n)
代入递推式:
J(2n+1)=2J(n)+1,J(2n)=2J(n)−1 J(2n+1) = 2J(n) + 1,\quad J(2n) = 2J(n) - 1 J(2n+1)=2J(n)+1,J(2n)=2J(n)−1
所以:
H(2n)=(2J(n)+1)−(2J(n)−1)=2 H(2n) = (2J(n) + 1) - (2J(n) - 1) = 2 H(2n)=(2J(n)+1)−(2J(n)−1)=2因此,对所有n≥1n \geq 1n≥1,有:
H(2n)=2 H(2n) = 2 H(2n)=2 -
H(2n+1)=J(2n+2)−J(2n+1)H(2n+1) = J(2n+2) - J(2n+1)H(2n+1)=J(2n+2)−J(2n+1)
J(2n+2)=J(2(n+1))=2J(n+1)−1J(2n+1)=2J(n)+1 J(2n+2) = J(2(n+1)) = 2J(n+1) - 1 \\ J(2n+1) = 2J(n) + 1 J(2n+2)=J(2(n+1))=2J(n+1)−1J(2n+1)=2J(n)+1
所以:
H(2n+1)=(2J(n+1)−1)−(2J(n)+1)=2(J(n+1)−J(n))−2=2H(n)−2 H(2n+1) = (2J(n+1) - 1) - (2J(n) + 1) = 2(J(n+1) - J(n)) - 2 = 2H(n) - 2 H(2n+1)=(2J(n+1)−1)−(2J(n)+1)=2(J(n+1)−J(n))−2=2H(n)−2即:
H(2n+1)=2H(n)−2,for n≥1 H(2n+1) = 2H(n) - 2, \quad \text{for } n \geq 1 H(2n+1)=2H(n)−2,for n≥1
错误推理分析
有人提出:可以对nnn使用归纳法,证明对所有nnn有H(n)=2H(n) = 2H(n)=2。
错误推理过程(伪证):
- 假设对所有k<nk < nk<n,有H(k)=2H(k) = 2H(k)=2
- 若nnn是偶数,n=2kn = 2kn=2k,则H(n)=H(2k)=2H(n) = H(2k) = 2H(n)=H(2k)=2
- 若nnn是奇数,n=2k+1n = 2k+1n=2k+1,则
H(2k+1)=2H(k)−2H(2k+1) = 2H(k) - 2H(2k+1)=2H(k)−2,由归纳假设H(k)=2H(k) = 2H(k)=2,得
H(2k+1)=2⋅2−2=2H(2k+1) = 2 \cdot 2 - 2 = 2H(2k+1)=2⋅2−2=2 - 故对所有nnn,H(n)=2H(n) = 2H(n)=2
问题出在哪儿?
虽然归纳步骤在形式上成立,但归纳法的基础没有验证。
我们检查小值:
计算J(n)J(n)J(n)和H(n)H(n)H(n)的前几项:
| nnn | J(n)J(n)J(n) | H(n)=J(n+1)−J(n)H(n) = J(n+1) - J(n)H(n)=J(n+1)−J(n) |
|---|---|---|
| 1 | 1 | H(1)=J(2)−J(1)H(1) = J(2) - J(1)H(1)=J(2)−J(1) |
| 2 | 2J(1)−1=12J(1)-1 = 12J(1)−1=1 | H(2)=J(3)−J(2)H(2) = J(3)-J(2)H(2)=J(3)−J(2) |
| 3 | 2J(1)+1=32J(1)+1 = 32J(1)+1=3 | H(3)=J(4)−J(3)H(3) = J(4)-J(3)H(3)=J(4)−J(3) |
| 4 | 2J(2)−1=2⋅1−1=12J(2)-1 = 2\cdot1 -1 = 12J(2)−1=2⋅1−1=1 | H(4)=J(5)−J(4)H(4) = J(5)-J(4)H(4)=J(5)−J(4) |
| 5 | 2J(2)+1=2⋅1+1=32J(2)+1 = 2\cdot1 +1 = 32J(2)+1=2⋅1+1=3 |
继续:
- H(1)=J(2)−J(1)=1−1=0≠2H(1) = J(2) - J(1) = 1 - 1 = 0 \ne 2H(1)=J(2)−J(1)=1−1=0=2
- H(2)=J(3)−J(2)=3−1=2H(2) = J(3) - J(2) = 3 - 1 = 2H(2)=J(3)−J(2)=3−1=2
- H(3)=J(4)−J(3)=1−3=−2H(3) = J(4) - J(3) = 1 - 3 = -2H(3)=J(4)−J(3)=1−3=−2
- H(4)=J(5)−J(4)=3−1=2H(4) = J(5) - J(4) = 3 - 1 = 2H(4)=J(5)−J(4)=3−1=2
可见:
- H(1)=0≠2H(1) = 0 \ne 2H(1)=0=2
- H(3)=−2≠2H(3) = -2 \ne 2H(3)=−2=2
因此,归纳基础不成立。
虽然归纳步骤在n≥2n \geq 2n≥2时可能成立,但当n=1n = 1n=1时H(1)≠2H(1) \ne 2H(1)=2,导致整个归纳失败。
根本错误
- 归纳法没有验证基础情况:H(1)=0≠2H(1) = 0 \ne 2H(1)=0=2,但推理中隐含地假设了H(n)=2H(n) = 2H(n)=2对所有nnn成立,包括基础情形;
- 虽然H(2n)=2H(2n) = 2H(2n)=2恒成立,但H(2n+1)=2H(n)−2H(2n+1) = 2H(n) - 2H(2n+1)=2H(n)−2依赖于H(n)H(n)H(n)的值,而H(1)=0H(1) = 0H(1)=0会导致H(3)=2⋅0−2=−2H(3) = 2 \cdot 0 - 2 = -2H(3)=2⋅0−2=−2,与H(n)=2H(n) = 2H(n)=2矛盾。
最终答案:该推理的错误在于未验证归纳
作业题
Exercise 8
题目:解递归式
Q0=α;Q1=β;
Q_0 = \alpha; \quad Q_1 = \beta;
Q0=α;Q1=β;
Qn=1+Qn−1Qn−2,n>1.
Q_n = \frac{1 + Q_{n-1}}{Q_{n-2}}, \quad n > 1.
Qn=Qn−21+Qn−1,n>1.
假设对所有 n≥0n \geq 0n≥0 都有 Qn≠0Q_n \ne 0Qn=0。提示:Q4=(1+α)/βQ_4 = (1 + \alpha)/\betaQ4=(1+α)/β。
解题思路
我们通过逐项计算前几项,观察序列是否具有周期性。由于递归式是非线性的,难以直接求解通项,但可能呈现周期性。
逐步计算
已知:
- Q0=αQ_0 = \alphaQ0=α
- Q1=βQ_1 = \betaQ1=β
计算后续项:
-
Q2=1+Q1Q0=1+βαQ_2 = \dfrac{1 + Q_1}{Q_0} = \dfrac{1 + \beta}{\alpha}Q2=Q01+Q1=α1+β
-
Q3=1+Q2Q1=1+1+βαβ=α+1+βαβ=1+α+βαβQ_3 = \dfrac{1 + Q_2}{Q_1} = \dfrac{1 + \dfrac{1 + \beta}{\alpha}}{\beta} = \dfrac{\dfrac{\alpha + 1 + \beta}{\alpha}}{\beta} = \dfrac{1 + \alpha + \beta}{\alpha\beta}Q3=Q11+Q2=β1+α1+β=βαα+1+β=αβ1+α+β
-
Q4=1+Q3Q2=1+1+α+βαβ1+βα=αβ+1+α+βαβ1+βα=(αβ+α+β+1)ααβ(1+β)Q_4 = \dfrac{1 + Q_3}{Q_2} = \dfrac{1 + \dfrac{1 + \alpha + \beta}{\alpha\beta}}{\dfrac{1 + \beta}{\alpha}} = \dfrac{\dfrac{\alpha\beta + 1 + \alpha + \beta}{\alpha\beta}}{\dfrac{1 + \beta}{\alpha}} = \dfrac{(\alpha\beta + \alpha + \beta + 1)\alpha}{\alpha\beta(1 + \beta)}Q4=Q21+Q3=α1+β1+αβ1+α+β=α1+βαβαβ+1+α+β=αβ(1+β)(αβ+α+β+1)α
化简分子:α(αβ+α+β+1)=α[(α+1)(β+1)]\alpha(\alpha\beta + \alpha + \beta + 1) = \alpha[(\alpha+1)(\beta+1)]α(αβ+α+β+1)=α[(α+1)(β+1)]
分母:αβ(1+β)\alpha\beta(1 + \beta)αβ(1+β)
但更直接代入数值或保留表达式:
我们使用提示:Q4=1+αβQ_4 = \dfrac{1 + \alpha}{\beta}Q4=β1+α
验证是否一致(略去复杂代数,接受提示或验证成立),继续:
-
Q5=1+Q4Q3=1+1+αβ1+α+βαβ=β+1+αβ1+α+βαβ=(1+α+β)β⋅αβ1+α+β=αQ_5 = \dfrac{1 + Q_4}{Q_3} = \dfrac{1 + \dfrac{1 + \alpha}{\beta}}{\dfrac{1 + \alpha + \beta}{\alpha\beta}} = \dfrac{\dfrac{\beta + 1 + \alpha}{\beta}}{\dfrac{1 + \alpha + \beta}{\alpha\beta}} = \dfrac{(1 + \alpha + \beta)}{\beta} \cdot \dfrac{\alpha\beta}{1 + \alpha + \beta} = \alphaQ5=Q31+Q4=αβ1+α+β1+β1+α=αβ1+α+βββ+1+α=β(1+α+β)⋅1+α+βαβ=α
-
Q6=1+Q5Q4=1+α1+αβ=βQ_6 = \dfrac{1 + Q_5}{Q_4} = \dfrac{1 + \alpha}{\dfrac{1 + \alpha}{\beta}} = \betaQ6=Q41+Q5=β1+α1+α=β
-
Q7=1+Q6Q5=1+βα=Q2Q_7 = \dfrac{1 + Q_6}{Q_5} = \dfrac{1 + \beta}{\alpha} = Q_2Q7=Q51+Q6=α1+β=Q2
-
Q8=1+Q7Q6=1+1+βαβ=Q3Q_8 = \dfrac{1 + Q_7}{Q_6} = \dfrac{1 + \dfrac{1 + \beta}{\alpha}}{\beta} = Q_3Q8=Q61+Q7=β1+α1+β=Q3
-
Q9=1+Q8Q7=1+Q3Q2=Q4Q_9 = \dfrac{1 + Q_8}{Q_7} = \dfrac{1 + Q_3}{Q_2} = Q_4Q9=Q71+Q8=Q21+Q3=Q4
-
Q10=1+Q9Q8=1+Q4Q3=Q5=αQ_{10} = \dfrac{1 + Q_9}{Q_8} = \dfrac{1 + Q_4}{Q_3} = Q_5 = \alphaQ10=Q81+Q9=Q31+Q4=Q5=α
-
Q11=1+Q10Q9=1+αQ4=1+α(1+α)/β=βQ_{11} = \dfrac{1 + Q_{10}}{Q_9} = \dfrac{1 + \alpha}{Q_4} = \dfrac{1 + \alpha}{(1 + \alpha)/\beta} = \betaQ11=Q91+Q10=Q41+α=(1+α)/β1+α=β
观察周期性
列出结果:
| nnn | QnQ_nQn |
|---|---|
| 0 | α\alphaα |
| 1 | β\betaβ |
| 2 | 1+βα\dfrac{1 + \beta}{\alpha}α1+β |
| 3 | 1+α+βαβ\dfrac{1 + \alpha + \beta}{\alpha\beta}αβ1+α+β |
| 4 | 1+αβ\dfrac{1 + \alpha}{\beta}β1+α |
| 5 | α\alphaα |
| 6 | β\betaβ |
| 7 | 1+βα=Q2\dfrac{1 + \beta}{\alpha} = Q_2α1+β=Q2 |
| 8 | Q3Q_3Q3 |
| 9 | Q4Q_4Q4 |
| 10 | Q5=αQ_5 = \alphaQ5=α |
| 11 | Q6=βQ_6 = \betaQ6=β |
可见:从 Q5Q_5Q5 开始,Q5=Q0=αQ_5 = Q_0 = \alphaQ5=Q0=α,Q6=Q1=βQ_6 = Q_1 = \betaQ6=Q1=β,且递归式仅依赖前两项,因此序列从 n=5n=5n=5 起重复 n=0n=0n=0 开始的模式。
即:
Qn+5=Qn对所有 n≥0
Q_{n+5} = Q_n \quad \text{对所有 } n \geq 0
Qn+5=Qn对所有 n≥0
但更准确地:
- Q5=Q0Q_5 = Q_0Q5=Q0
- Q6=Q1Q_6 = Q_1Q6=Q1
- Q7=Q2Q_7 = Q_2Q7=Q2
- …\dots…
所以序列从 n=0n=0n=0 开始,周期为 5。
结论
序列 {Qn}\{Q_n\}{Qn} 是周期为 5 的周期序列,即:
Qn+5=Qn,对所有 n≥0
Q_{n+5} = Q_n, \quad \text{对所有 } n \geq 0
Qn+5=Qn,对所有 n≥0
前六项为:
- Q0=αQ_0 = \alphaQ0=α
- Q1=βQ_1 = \betaQ1=β
- Q2=1+βαQ_2 = \dfrac{1 + \beta}{\alpha}Q2=α1+β
- Q3=1+α+βαβQ_3 = \dfrac{1 + \alpha + \beta}{\alpha\beta}Q3=αβ1+α+β
- Q4=1+αβQ_4 = \dfrac{1 + \alpha}{\beta}Q4=β1+α
- Q5=α=Q0Q_5 = \alpha = Q_0Q5=α=Q0
- Q6=β=Q1Q_6 = \beta = Q_1Q6=β=Q1
最终答案:序列 QnQ_nQn 是周期为 5 的周期序列,即 Qn+5=QnQ_{n+5} = Q_nQn+5=Qn,对所有 n≥0n \geq 0n≥0 成立。
Exercise 9
题目:有时可以利用反向归纳法,它从 nnn 到 n−1n-1n−1 来证明命题,而不是通常的从小到大。考虑命题
P(n):x1⋯xn≤(x1+⋯+xnn)n,x1,…,xn≥0.
P(n): \quad x_1 \cdots x_n \leq \left( \frac{x_1 + \cdots + x_n}{n} \right)^n, \quad x_1, \ldots, x_n \geq 0.
P(n):x1⋯xn≤(nx1+⋯+xn)n,x1,…,xn≥0.
已知 P(2)P(2)P(2) 成立,因为 (x1+x2)2−4x1x2=(x1−x2)2≥0(x_1 + x_2)^2 - 4x_1x_2 = (x_1 - x_2)^2 \geq 0(x1+x2)2−4x1x2=(x1−x2)2≥0,即
x1x2≤(x1+x22)2.
x_1 x_2 \leq \left( \frac{x_1 + x_2}{2} \right)^2.
x1x2≤(2x1+x2)2.
(a) 设 x=x1+⋯+xn−1n−1x = \frac{x_1 + \cdots + x_{n-1}}{n-1}x=n−1x1+⋯+xn−1,证明只要 n>1n > 1n>1,P(n)P(n)P(n) 蕴涵 P(n−1)P(n-1)P(n−1)。
(b) 证明 P(n)P(n)P(n) 和 P(2)P(2)P(2) 蕴涵 P(2n)P(2n)P(2n)。
© 说明为什么这就蕴涵了 P(n)P(n)P(n) 对所有 nnn 为真。
(a) 证明 P(n)⇒P(n−1)P(n) \Rightarrow P(n-1)P(n)⇒P(n−1)(反向归纳)
假设 P(n)P(n)P(n) 成立,即对任意非负实数 y1,…,yn≥0y_1, \ldots, y_n \geq 0y1,…,yn≥0,
y1y2⋯yn≤(y1+⋯+ynn)n.
y_1 y_2 \cdots y_n \leq \left( \frac{y_1 + \cdots + y_n}{n} \right)^n.
y1y2⋯yn≤(ny1+⋯+yn)n.
要证 P(n−1)P(n-1)P(n−1):对任意 x1,…,xn−1≥0x_1, \ldots, x_{n-1} \geq 0x1,…,xn−1≥0,
x1⋯xn−1≤(x1+⋯+xn−1n−1)n−1.
x_1 \cdots x_{n-1} \leq \left( \frac{x_1 + \cdots + x_{n-1}}{n-1} \right)^{n-1}.
x1⋯xn−1≤(n−1x1+⋯+xn−1)n−1.
令
x=x1+⋯+xn−1n−1
x = \frac{x_1 + \cdots + x_{n-1}}{n-1}
x=n−1x1+⋯+xn−1
为前 n−1n-1n−1 个变量的算术平均。
在 P(n)P(n)P(n) 中,取:
- y1=x1,…,yn−1=xn−1y_1 = x_1, \ldots, y_{n-1} = x_{n-1}y1=x1,…,yn−1=xn−1,
- yn=xy_n = xyn=x
则由 P(n)P(n)P(n):
y1⋯yn=(x1⋯xn−1)⋅x≤(x1+⋯+xn−1+xn)n
y_1 \cdots y_n = (x_1 \cdots x_{n-1}) \cdot x \leq \left( \frac{x_1 + \cdots + x_{n-1} + x}{n} \right)^n
y1⋯yn=(x1⋯xn−1)⋅x≤(nx1+⋯+xn−1+x)n
由于 x1+⋯+xn−1=(n−1)xx_1 + \cdots + x_{n-1} = (n-1)xx1+⋯+xn−1=(n−1)x,分子为:
(n−1)x+x=nx
(n-1)x + x = nx
(n−1)x+x=nx
右边为:
(nxn)n=xn
\left( \frac{nx}{n} \right)^n = x^n
(nnx)n=xn
所以:
(x1⋯xn−1)⋅x≤xn
(x_1 \cdots x_{n-1}) \cdot x \leq x^n
(x1⋯xn−1)⋅x≤xn
若 x>0x > 0x>0,两边除以 xxx 得:
x1⋯xn−1≤xn−1=(x1+⋯+xn−1n−1)n−1
x_1 \cdots x_{n-1} \leq x^{n-1} = \left( \frac{x_1 + \cdots + x_{n-1}}{n-1} \right)^{n-1}
x1⋯xn−1≤xn−1=(n−1x1+⋯+xn−1)n−1
若 x=0x = 0x=0,则所有 xi=0x_i = 0xi=0,左边为 0,右边为 0,不等式成立。
因此 P(n−1)P(n-1)P(n−1) 成立。
结论:P(n)⇒P(n−1)P(n) \Rightarrow P(n-1)P(n)⇒P(n−1) 对所有 n>1n > 1n>1 成立。
(b) 证明 P(n)P(n)P(n) 和 P(2)P(2)P(2) 蕴涵 P(2n)P(2n)P(2n)(向前归纳)
假设 P(n)P(n)P(n) 和 P(2)P(2)P(2) 成立。要证 P(2n)P(2n)P(2n):
x1⋯x2n≤(x1+⋯+x2n2n)2n
x_1 \cdots x_{2n} \leq \left( \frac{x_1 + \cdots + x_{2n}}{2n} \right)^{2n}
x1⋯x2n≤(2nx1+⋯+x2n)2n
将变量分为两组:
- 第一组:x1,…,xnx_1, \ldots, x_nx1,…,xn
- 第二组:xn+1,…,x2nx_{n+1}, \ldots, x_{2n}xn+1,…,x2n
令:
- A=x1+⋯+xnnA = \frac{x_1 + \cdots + x_n}{n}A=nx1+⋯+xn
- B=xn+1+⋯+x2nnB = \frac{x_{n+1} + \cdots + x_{2n}}{n}B=nxn+1+⋯+x2n
由 P(n)P(n)P(n) 应用于每组:
x1⋯xn≤An,xn+1⋯x2n≤Bn⇒x1⋯x2n≤(AB)n
x_1 \cdots x_n \leq A^n, \quad x_{n+1} \cdots x_{2n} \leq B^n
\Rightarrow x_1 \cdots x_{2n} \leq (AB)^n
x1⋯xn≤An,xn+1⋯x2n≤Bn⇒x1⋯x2n≤(AB)n
由 P(2)P(2)P(2):AB≤(A+B2)2AB \leq \left( \frac{A + B}{2} \right)^2AB≤(2A+B)2
所以:
(AB)n≤((A+B2)2)n=(A+B2)2n
(AB)^n \leq \left( \left( \frac{A + B}{2} \right)^2 \right)^n = \left( \frac{A + B}{2} \right)^{2n}
(AB)n≤((2A+B)2)n=(2A+B)2n
而:
A+B2=12(A+B)=12(S1n+S2n)=S1+S22n=x1+⋯+x2n2n
\frac{A + B}{2} = \frac{1}{2} \left( A + B \right) = \frac{1}{2} \left( \frac{S_1}{n} + \frac{S_2}{n} \right) = \frac{S_1 + S_2}{2n} = \frac{x_1 + \cdots + x_{2n}}{2n}
2A+B=21(A+B)=21(nS1+nS2)=2nS1+S2=2nx1+⋯+x2n
因此:
x1⋯x2n≤(x1+⋯+x2n2n)2n
x_1 \cdots x_{2n} \leq \left( \frac{x_1 + \cdots + x_{2n}}{2n} \right)^{2n}
x1⋯x2n≤(2nx1+⋯+x2n)2n
即 P(2n)P(2n)P(2n) 成立。
结论:P(n)P(n)P(n) 和 P(2)P(2)P(2) 蕴涵 P(2n)P(2n)P(2n)。
© 为什么 P(n)P(n)P(n) 对所有 nnn 成立?
我们有以下两个推理方向:
- 向前:P(n)⇒P(2n)P(n) \Rightarrow P(2n)P(n)⇒P(2n)
- 向后:P(n)⇒P(n−1)P(n) \Rightarrow P(n-1)P(n)⇒P(n−1)(对 n>1n > 1n>1)
已知 P(2)P(2)P(2) 成立。
- 由 P(2)⇒P(4)⇒P(8)⇒⋯P(2) \Rightarrow P(4) \Rightarrow P(8) \Rightarrow \cdotsP(2)⇒P(4)⇒P(8)⇒⋯,可得 P(2k)P(2^k)P(2k) 对所有 k≥1k \geq 1k≥1 成立。
- 对任意正整数 mmm,存在 kkk 使得 m<2km < 2^km<2k。
- 由于 P(2k)P(2^k)P(2k) 成立,反复应用反向归纳:
P(2k)⇒P(2k−1)⇒⋯⇒P(m) P(2^k) \Rightarrow P(2^k - 1) \Rightarrow \cdots \Rightarrow P(m) P(2k)⇒P(2k−1)⇒⋯⇒P(m)
可得 P(m)P(m)P(m) 成立。
因此,P(n)P(n)P(n) 对所有正整数 nnn 成立。
例如:
- P(2)P(2)P(2) → P(4)P(4)P(4) → P(3)P(3)P(3)(由 P(4)⇒P(3)P(4) \Rightarrow P(3)P(4)⇒P(3))
- P(3)P(3)P(3) 和 P(2)P(2)P(2) → P(6)P(6)P(6)
- P(6)P(6)P(6) → P(5)P(5)P(5)
- P(5)P(5)P(5) 和 P(2)P(2)P(2) → P(10)P(10)P(10)
- 如此继续,可覆盖所有 nnn
最终答案:
(a) 通过将第 nnn 个变量设为前 n−1n-1n−1 个变量的算术平均,并应用 P(n)P(n)P(n),可推出 P(n−1)P(n-1)P(n−1)。
(b) 将 2n2n2n 个变量分为两组,分别应用 P(n)P(n)P(n),再结合 P(2)P(2)P(2),可推出 P(2n)P(2n)P(2n)。
© 由 P(2)P(2)P(2) 出发,通过向前归纳得到所有 2k2^k2k 的情形,再通过反向归纳覆盖所有更小的 nnn,从而 P(n)P(n)P(n) 对所有正整数 nnn 成立。




















 5056
5056

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








