误差对代数侧信道分析的影响

误差对代数侧信道分析中汉明重量的影响

1 引言

诸如侧信道分析（SCA）之类的攻击会观测系统泄漏的功耗等信息，并利用这些信息来破解算法。功耗分析攻击假设不同的数据和操作会消耗不同量的功耗。由于加密算法的输入包括明文和密钥，因此密钥与任何中间值的泄漏之间存在相关性。通过足够的数据，攻击者能够使用分而治之策略获取密钥。功耗分析攻击最初由[7]提出，并成功应用于数据加密标准（DES）。此后，该攻击也被证明对高级加密标准（AES）的所有常见模式（ECB、CBC、CFB、OFB 和 CTR）有效[6]，以及用于基于扇区的设备数据保护的高级模式XTS‐AES，该模式为每个数据块使用两个密钥和一个额外的调整参数[9]。由于此类攻击针对的是加密算法的实现，即使数学上最安全的算法仍可能受到此类攻击的影响。

然而，攻击的成功取决于侧信道数据的质量和数量。由于测量限制和噪声引起的误差，即使采用复杂的信号处理方法，该攻击通常也需要数百甚至数千条轨迹。

处理方法 [8,13,25,26]。一种较新的方法是将侧信道分析与代数分析相结合[20]。这种攻击将加密算法和侧信道信息建模为一组方程。然后将这些方程输入求解器以求解密钥。代数侧信道分析不仅比纯侧信道分析需要更少的信息，而且在明文/密文未知的情况下也能成功，而侧信道分析则需要知道明文或密文。代数侧信道分析还可以利用算法所有轮次的泄露信息，而侧信道分析只能攻击第一轮或最后一轮。侧信道分析采用分而治之的策略，一次恢复一个字节的密钥，而代数侧信道分析具有较低的数据复杂度，能够一次性恢复整个密钥。

尽管代数侧信道分析（ASCA）使用的信息少于侧信道分析（SCA），但由于来自SCA信息的噪声，它仍然容易受到误差的影响，可能导致不准确的解并增加运行时间。根据模型或方程的规模和复杂性，它也可能具有较高的内存消耗。纯ASCA被建模为一组布尔方程，并使用SAT求解器进行求解。然而，将带有误差的侧信道信息建模为SAT实例较为困难，且非线性操作会显著增加系统的复杂性。[14]没有采用SAT方法，而是将方程建模为考虑误差的非线性伪布尔优化问题，并成功对Keeloq实施了攻击。该求解器能够在18.8%的误差下找到密钥，平均运行时间为3.8小时。另一项攻击在[16]中使用约束求解器 SCIPspx来选择最可能的中间状态而非最可能的密钥。由于信息具有一定的冗余性，因此可以容忍单个状态元素恢复时较低的准确性，从而能够100%获得正确密钥。成功攻击的中位数时间为607秒，最长为6小时。另一种方法SASCA在 [27]中被提出，其中AES Furious和模板信息被建模为因子图，可通过置信传播算法高效解码，从而从低密度奇偶校验码中找出最可能的密钥。在[5]中比较了基于真实数据的SASCA、ASCA和DPA的性能。SASCA的表现优于ASCA，但通常比分治法（DPA）攻击计算量更大。当有大量轨迹可用时，SASCA相对于DPA的优势有限。如果明文或密文未知，则SASCA可能是最佳选择。可利用的泄漏样本的数量和类型决定了SASCA的强大程度。ASCA的求解时间取决于信息量，而在SASCA中则与此信息量无关。

我们的模型利用了约束编程。通过在约束编程模型中使用位向量，密码算法方程组的复杂性大大降低，从而改善了运行时间。即使存在多个满足模型的解，其他求解器也只能输出一个解，该解可能正确也可能不正确，而我们使用的Objective‐C求解器能够输出所有解。由于攻击在内存和运行时间方面的劣势已不再明显，这使得我们能够更深入地探索该攻击。除了减少运行时间之外，另一个值得关注的点是攻击所需的侧信道信息。本文中，我们评估了关于侧信道信息的模型，以及不同子轮的信息如何影响攻击的效果。这不仅将帮助我们更好地理解攻击，并了解误差在何处产生影响，还可能为需要重点保护的内容提供见解，并有助于未来的对抗措施。

本文的其余部分组织如下：第2节概述容错代数侧信道分析（TASCA）攻击。第3节简要介绍攻击模型。第4节说明我们实现该攻击的实验设置。第5节描述实验和结果。最后，第6节对全文进行总结。

2 容错代数侧信道分析

TASCA攻击假设攻击者可以访问一个在加密或解密过程中产生可测量的侧信道泄漏（如功耗）的被测设备（DUT）。该功耗应可通过示波器进行采集，且错误率在求解器可处理的范围内。TASCA方法通过以下步骤从功率轨迹中恢复密钥：

– Identify potential leaks。此处使用的侧信道泄漏为功耗轨迹。大多数智能卡处理器采用CMOS电路实现，其中门切换会引起可观测的电流。汉明重量模型通过统计切换次数，用于建模功率轨迹与和密钥相关的中间变量之间的关系。虽然大多数侧信道信息基于8位微控制器，但侧信道信息仍可被获取并用于攻击大多数使用CMOS电路的设备。先前的研究[19,23,24],表明，功耗分析攻击的变种能够成功攻破在FPGA上实现的椭圆曲线密码、数据加密标准和 RSA。该攻击也已在专用集成电路[18],STC89C52微处理器[4]以及 Cortex‐M3 CPU [1]上实现的高级加密标准中得到验证。

– 分析被测设备并设计解码过程。 本文的目标加密算法是AES‐128。侧信道泄漏，即功率轨迹，是通过模板攻击获取的。在模板攻击中，攻击者应拥有与被测设备相同的实验设备，并能够从该设备收集大量侧信道信息（通常为数千条功率轨迹）。利用这些信息，攻击者使用多元高斯模型设计一个解码过程，将侧信道信息映射到算法[16]中中间值的汉明重量。

– 从被测设备获取功率轨迹并解码汉明重量。在此阶段，攻击者通过示波器访问实际的被测设备，从中收集几条功率轨迹。前一步骤中的模板被用作参考，以从功率轨迹中提取汉明重量。

由于高级加密标准采用字节级操作，每个泄漏的汉明重量表示为一个介于0到8之间的整数。

– 将被测设备和侧信道信息建模为一组代数方程。 被测设备（即AES‐128）的形式化描述、来自侧信道信息的汉明重量以及误差变量都被表示为一个方程组。

– 求解密钥。 给定该模型，以及所需的明文或密文，求解器将寻找满足该模型的解，该解应为正确的密钥。

攻击的目标是使用最少的信息量并在合理时间内以高成功率获取密钥。

3 攻击模型

高级加密标准是一种应用最广泛且研究最多的分组密码。本文研究的变体是 AES‐128。它以128比特的数据块作为输入（明文），将其排列成4×4字节的状态，然后与密钥进行组合。输出需经过10轮次的操作，最终生成密文，如图1所示。

每轮 AES 包含以下四个子轮，如图2所示。

有关高级加密标准结构的更多详细信息，请参见[2]。高级加密标准算法以及侧信道信息均使用位向量和约束编程模型[11]进行描述。通过这种方式，我们可以采用更直接且自然的表述形式，而无需进行线性化处理。

3.1 变量

每个状态变量由16个8位宽的位向量表示。高级加密标准的许多子轮操作（如字节替换和列混淆）都是对8位值进行操作，因此本模型使用8位宽的位向量。侧信道信息和高级加密标准算法的状态被建模为以下决策变量：

– 状态变量 Ssr,i,j对应于每个中间状态。Ssr,i,j表示在子轮 sr中状态字节 i的第 j位的值，其中 sr ∈[0, 40], i ∈[0, 15],j ∈[0, 7]。 S0表示初始明文， S40表示密文。

– 密钥变量 Kr,i,j对应于128位密钥。Kr,i,j表示第 r轮密钥字节 i的第 j位的值，其中 r ∈[0, 10], i ∈[0, 15], j ∈[0, 7]。 K0指密码密钥，而 Kr(r> 0)指通过密钥扩展从密码密钥派生出的轮密钥。– 误差变量Esr,i放宽了SCA约束，以考虑旁道方程中的噪声。在初始实验中，状态变量的实际值允许偏离测量值 ±1 ，在后续实验中偏离 ±2，以覆盖更现实的误差范围。变量Esr,0表示正误差，变量Esr,1表示负误差。

3.2 约束

– 轮密钥加/轮密钥加将状态与通过密钥扩展从密钥导出的轮密钥进行异或。该操作通过两个输入位向量之间的按位异或运算实现。状态的每个字节由以下约束表示：

Ssr,i ⊕ Ksr,i= Ssr+1,i, ∀i={0,…, 15}

– SubByte根据查找表或S盒将状态的每个字节替换为另一个字节。它通过位向量上的元素约束来实现。SubByte约束通过一个位向量上的元素约束对置换 π进行建模：

SBox[A]= B

– 行移位 & 列混淆将状态的四行分别向左移动0、1、2和3个字节，然后将每一列与一个常数矩阵(MC)相乘。这两个操作被合并在一起，并在约束规划编码中使用了8比特高效的列混淆实现。采用位向量约束来表示异或以及 xtime，从而得到每一列的如下结果：

βk= xtime(ak ⊕ a(k+1) mod 4) ∀ k ∈ 0..3
ok=( 3 ⊕
i=0 ai)⊕ βk ⊕ ak ∀ k ∈ 0..3

– 密钥扩展 负责从密码密钥生成轮密钥加操作中使用的轮密钥。为每一轮创建一组表示轮常数的位向量变量 rconi。使用字节替换和异或约束来生成轮密钥。

以下是密钥扩展的编码：

Kr,0= SubByte(Kr−1,13)⊕ Kr−1,0 ⊕ RCr
Kr,1= Kr−1,1 ⊕ SubByte(Kr−1,14)
Kr,2= Kr−1,2 ⊕ SubByte(Kr−1,15)
Kr,3= Kr−1,3 ⊕ SubByte(Kr−1,12)
Kr,i+4= Kr,i ⊕ Kr−1,i+4, ∀i={0,…, 11}

– 侧信道约束 由汉明重量向量生成。count 约束用于统计比特向量中值为1的比特位数，表示实际的汉明重量。约束 Msr,i 表示包含误差的汉明重量：

count(Ssr,i)+ e+ sr,i − e− sr,i= Msr,i

– 目标函数 被建模为错误总数，与整数规划模型相同：

Min: ∑ e + sr,i +∑ e − sr,i

除了提供一组汉明重量（HW）以考虑误差外，TASCA 还更进一步，在目标函数中优先选择最有可能的汉明重量进行分支/搜索。

3.3 搜索

除了表示高级加密标准和汉明重量的方程外，TASCA模型的CP版本的一个重要部分是搜索，该搜索用于优化来自汉明重量的误差。在高级加密标准加密过程中，每个状态字节都会生成一个作为侧信道信息的汉明重量。候选值v ∈ D (Sr,i)具有汉明重量 H(v) = ∑b∈0..7(v|b= 1)，用于表示 v中值为1的比特位数。

TASCA要求 D(Sr,i)被限制为满足条件的值 v
−1 ≤ H(v)− Mr,i ≤ 1
即，测量值 Mr,i 与值 v 之间的差异不超过 ±1。该约束规划模型的目标是最小化在汉明重量中可能出现的错误总数。在目标函数中产生最少错误的值分配上进行分支，将最有效地尽早获得高质量解。当目标函数等于误差之和时，我们有
min
41
∑
j=0 E(j, σ(Sj)) where E(j, v)={0 if H(v)= Mj
1 if H(v)= Mj ± 1
且 σ是当前值分配。

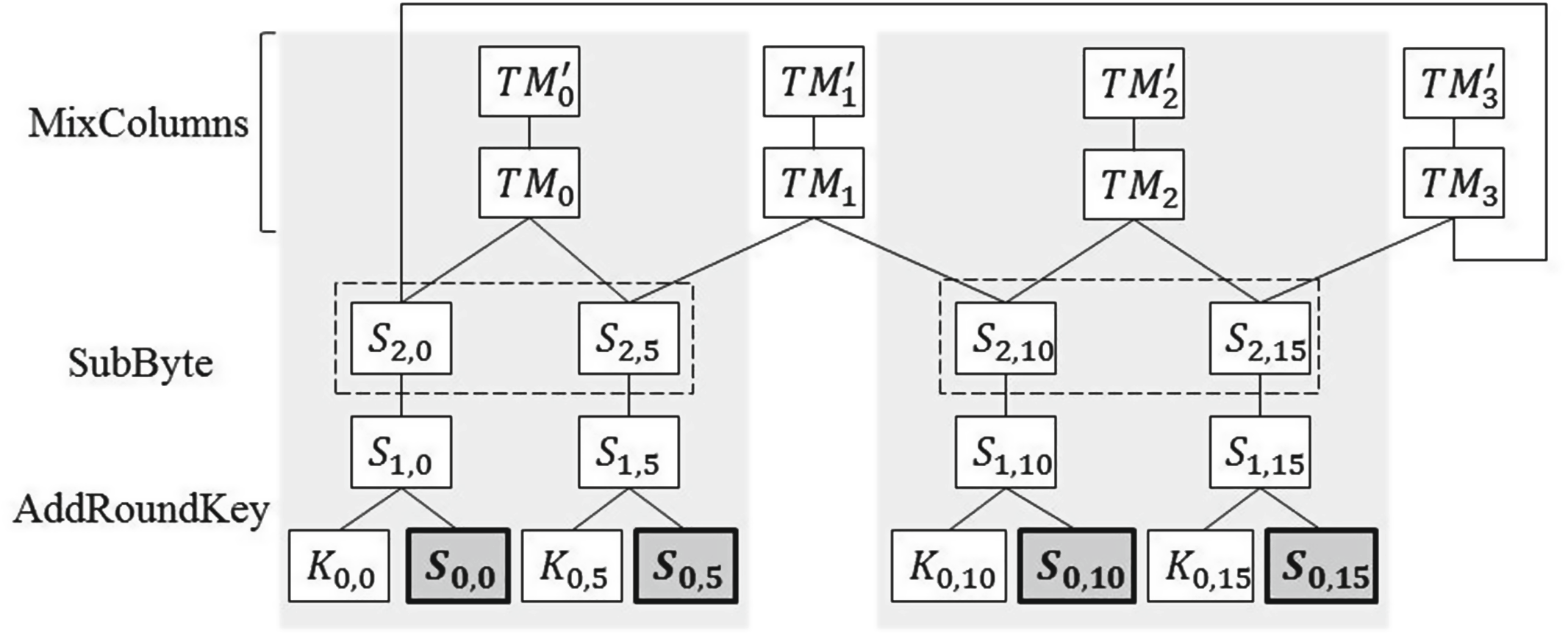
电路视图： 考虑包含全部4个子轮的高级加密标准算法单轮，轮密钥加、字节替换以及列混淆/行移位，图3展示了状态矩阵第一列的子轮。该结构在整个状态上重复四次。状态的列[S0,0S0,5S0,10S0,15] T和子轮密钥的列 [K0,0K0,5K0,10K0,15] T构成图底部的输入。在第1轮中，[S0,0S0,5S0,10S0,15] T是已知的，因为它们表示明文的字节。一旦状态已知，轮密钥加和字节替换将应用双射变换。因此，一旦S2,0,S1,0或K0,0被确定，其余值将通过传播被确定 （这对S2,5,S1,5和K0,5同样成立）。左侧包含S2,0和S2,5的虚线框突出显示了异或运算的输入产生临时值 T M0。电路 T M0′的输出是输出的第一个字节，即 状态S4,0。左侧垂直的浅灰色列为输出字节0所定义关系的描述。 T M0的计算依赖于S2,0和S2,5的值是否可用。注意，例如，如果S2,5被固定，则只需固定S2,10即可实现上下传播，并同时固定K0,10和 T M1′。

变量选择启发式：对 T M0进行分支仅会触发“向上”的传播，因为异或无法向下传递信息。类似地，对S2,0甚至K0,0进行分支，由于底部“支路”中关系的双射性质，其传播范围也将受限。然而，同时为虚线框中的两个变量赋值将触发向上和向下的传播。

这是变量选择策略的一个关键见解。搜索应分支于成对的变量 这些变量能在整个灰色框内触发传播。在图3中，这意味着共有四列，总共需要考虑16对变量作为首次分支决策（请注意该结构被复制了4次）。这四列的顶部变量为 T M′ 0, T M′ 1, T M′ 3。一旦选定了一个变量对，搜索应通过重用第一个变量对中的其中一个变量来创建另一个变量对。例如，如果选择了 〈S2,0,S2,5〉， 那么可以考虑接下来的两对变量 〈S2,5, S2,10〉 和 〈S2,15, S2,0〉，因为 T M1和 T M3的定义域会因第一次选择而缩小。

最后，请注意，并非从S2,0和S2,5的定义域中选取的所有值对都是兼容的。其中一些值对可能会导致误差超过TASCA规定的±1范围。因此，建议遵循首次失败原则，并根据产生符合误差范围的赋值的值对数量来打破变量对之间的平局。

值选择启发式： 目标函数中的误差由状态变量上的测量误差之和驱动。如果搜索考虑一对值
〈a, b〉 ∈ D(S2,0)× D(S2,5)
它可以评估同时赋值 S2,0= a ∧ S2,5= b 对最左侧灰色列中状态变量的误差所产生的影响。这种评估是对赋值所引起的真实误差的一种欠逼近。事实上， T M′ 1 可能会暴露出由于为 S2,5 选择值 b 而导致的错误，但该错误位于灰色列之外，因此被忽略。一种合理的值选择启发式会考虑值对，并使用评分函数 C 来评估其质量。给定一对值 〈a, b〉，其评分过程是
C(〈a, b〉)= Cleg(a,[S2,0, S1,0, K0,0])+Cleg(b,[S2,5, S1,5, K0,5])+Cmc(a⊕b,[T M′ 0])
函数Cleg 和 Cmc用于建模灰色框中一条支路或灰色框顶部（列混淆操作）的误差，而 a⊕ b表示基于连接的异或约束推断出的 T M0的值。 Cleg 和 Cmc用于度量状态变量的值与预期汉明重量之间的差异。给定一对变量和评分函数 C， 该值启发式方法会枚举对目标函数贡献最小的变量对。

最优性剪枝：由于汉明重量引起的误差贡献随着搜索深度的增加而累积，因此可以利用总误差进一步剪枝那些其贡献将导致总误差超过当前最优解总误差的值对。

4 实验设置

我们假设密钥扩展已经预先完成，并且该过程不会产生任何侧信道泄漏。这对应于一种更具挑战性的场景，因为已有研究在[10]中表明，在8位微控制器上实现高级加密标准时，密钥扩展过程中的侧信道泄漏足以恢复完整密钥。因此，本次攻击将聚焦于高级加密标准算法本身。我们的分析考虑了以8位微控制器上模拟实现的AES‐128作为被测设备（DUT）。在本实验所采用的TASCA与约束规划模型攻击中，使用的求解器是Objective‐CP[3]。

实验在配备 macOS Sierra 10.12.6、3.1 GHz Intel Core i5 处理器和 8GB 内存的 Mac 上运行。对于随机实例，明文在 {0, 1}^128 中均匀选择，密钥保持固定。每个实例包含一个已知明文和 100 个汉明重量，这些汉明重量对应于 AES 第一轮。

4.1 子轮比较

先前来自[17]的结果表明，如果泄漏数量减少到少于完整一轮，攻击成功的概率将变得极低。虽然[21]提到在求解系统时，列混淆的汉明重量似乎最为关键，但尚未开展实验来探究来自不同子轮的侧信道信息对攻击的影响。TASCA的一个优势是所需数据极少——在无误差情况下仅需1条迹线的1轮汉明重量。如果某些子轮的汉明重量比其他子轮更重要，那么当使用少于1轮的汉明重量时，攻击是否成功还将取决于遗漏了哪些汉明重量。由于TASCA考虑了误差量，我们可以通过在特定子轮引入误差来观察不同子轮对攻击成功率的影响。

4.2 误差容忍度

已经证明，在[21]中，通过使用误差检测（拒绝导致S盒输入/输出值不一致的侧信道信息）和似然评级（仅使用通过模板提取的所有汉明重量的一个子集，从最有可能的开始），可以从1条功率轨迹中以80%准确率获取汉明重量等侧信道信息。文献中的IASCA通过分析2000条攻击轨迹的分布来探究汉明重量的容错性。误差分布如表1所示。

错误类别	e0	e1	e2	e3	e4
出现次数	28%	44%	24%	4%	0%

误差变量 e0到 e4表示包含0到4个错误的汉明重量集合。错误类别 e0仅包含正确的汉明重量（HW）， e1是包含一个错误的汉明重量集合（HW, HW+1）， e2包含两个错误（HW−1, HW, HW+1）， e3包含三个错误（HW−1, HW, HW+1, HW+2），而e4包含五个错误（HW−2, HW−1, HW, HW+1, HW+2）。对于所有错误类别，均假设正确的汉明重量在该集合内。

5 结果

第一次实验测试了不同子轮对攻击成功率的影响。该实验在10个随机生成的实例上进行，给定第一轮的汉明重量。其中包括AddRoundKey的16字节汉明重量、SubByte的16字节汉明重量、ShiftRow无汉明重量以及MixColumn的 36字节汉明重量。通过在AddKey、SubByte或MixColumn的16字节上引入 ±1误差时的运行时间进行比较来开展实验。表2显示了平均求解时间、解池（满足模型的解的数量）以及成功率（在24小时内成功求解密钥的实例数量）。

存在 ±1误差的子轮	轮密钥加	字节替换	列混淆
求解时间	3,609.93 s	1,871.72 s	940.02 s
解池	8,470	39,323	1,217
成功率	80%	80%	60%

我们的求解器的一个独特之处在于它会输出所有可能的解，因此不会出现错误的解。它要么找不到解（解池为0），要么找到一个解或一组可能的解。[17]已经表明，遍历解集并找到正确密钥只需几秒钟，因此解池大小的差异不如求解时间和成功率重要。实验表明，当所有误差都集中在列混淆的信息上时，攻击更困难，或成功率更低；而当误差集中在轮密钥加和字节替换上时则相对容易。然而，在24小时内可求解密钥的随机实例中，列混淆的求解速度最快，其次是字节替换，最后是轮密钥加。

大多数先前的容错代数侧信道攻击（ASCA）通过使用多条轨迹并仅对误差属于±1或最多到错误类别 e2的汉明重量进行建模来最小化误差。然而，在某些情况下，该范围无法覆盖汉明重量误差的完整范围。将误差容忍度扩展至 e3 甚至 e4，可能使攻击能够利用单条轨迹或甚至在噪声测量条件下成功。由于 TASCA‐CP模型在错误类别最多为 e2和[3]时，在运行时间和内存使用上实现了数量级的提升，本文将该模型扩展至覆盖错误类别e3和 e4，以实现更实际的攻击。虽然我们最初计划在100%错误率下运行代码，但这种约束会抵消搜索函数的作用，导致求解器无法在24小时时间限制内找到解。由于通过某些数据处理可以获得80%准确率的汉明重量[21]，我们转而尝试20%的错误率，即20% 的汉明重量被分配了 −1、+1、 −2或+2的误差。该攻击在10个实例上进行，仅使用第一轮的汉明重量。具有错误类别 e3和 e4的汉明重量模型在[12,15,22]中进行了探索。表3展示了误差容忍度超过 ±1（e2）的代数侧信道分析（ASCA）结果。

	误差率	错误类别	求解时间	成功率	轮	轨
TASCA [15]	20%	e3	1332.07 秒	72.7%	R1	1
IASCA [12]	100%	e3	84 s	100%	R1–R3	1
IASCA [12]	100%	e4	100 秒	50%	R1	1
ETASCA[22]	100%	e4	33.29 秒	-	R1	3
TASCA‐CP	20%	e4	8.6 小时	50%	R1	1

所有攻击均使用已知明文/密文进行。误差率指具有误差的汉明重量的百分比。成功率指在合理时间内输出正确密钥的实例百分比。

6 结论

结果表明，对于成功攻击而言，某些子轮的侧信道信息确实比其他子轮更具影响力。虽然MixColumn子轮中的准确信息对TASCA的成功机会最为重要，但 SubByte存在误差的实例运行速度要快于AddRoundKey存在误差的实例。当攻击者面对包含不同错误的多条轨迹时，此信息非常有用，因为选择 MixColumn子轮中误差较小的轨迹或汉明重量轮次，可能会提高成功攻击的机会。本实验还为改进TASCA的对抗措施提供了依据。由于当前的对抗措施（如随机掩码）非常耗时，因此最好将重点放在特定子轮的侧信道信息掩码上。在我们的情况下，TASCA 的快速运行时间在很大程度上依赖于搜索算法，该算法通过分析不同子轮汉明重量之间误差的相关性来过滤掉可能性较小的汉明重量和误差。因此，当汉明重量的误差范围扩大到 ±2 时，需要更改搜索算法，且运行时间显著增加。

除了进一步改进搜索外，我们还将测试未知明文/密文情况下的容错代数侧信道攻击。目前尚无其他具有误差容忍度的代数侧信道分析在未知明文/密文情况下取得成功，而这一点正是TASCA相较于侧信道分析的一大优势。

定义一次成功攻击的最重要因素是：攻击应快速运行、使用较少的数据/信息且要求宽松，并具有较高的成功率。更高的误差容忍度即使在数据质量较低的情况下，也能提高攻击成功的可能性。然而，结果的差异可能是由于本次攻击中使用的不同求解器和模型所致，而非加密算法本身的属性。为了防止代数侧信道分析，要么需要提高加密算法的代数复杂度，要么应实施对抗措施以增加准确收集侧信道分析信息的难度。

除了本文所展示的内容之外，还有其他值得探索的研究方向。我们可以尝试不同的轮次而非第一轮，或者验证结果在其他分析方法或泄露模型下是否仍然成立。除了汉明重量之外，概率向量被提出作为一种更优的方式表示侧信道信息，以最小化数据丢失。我们还可以对AES‐256或其他AES版本（如 ECB/CBC等）发起攻击。由于侧信道分析对抗措施在设备中正逐渐普及，尝试在掩码版本上进行攻击将非常有意义（这需要了解功率轨迹中与中间值相关的汉明重量的确切位置以及掩码类型）。