Lecture 002-LP introduction

Outline

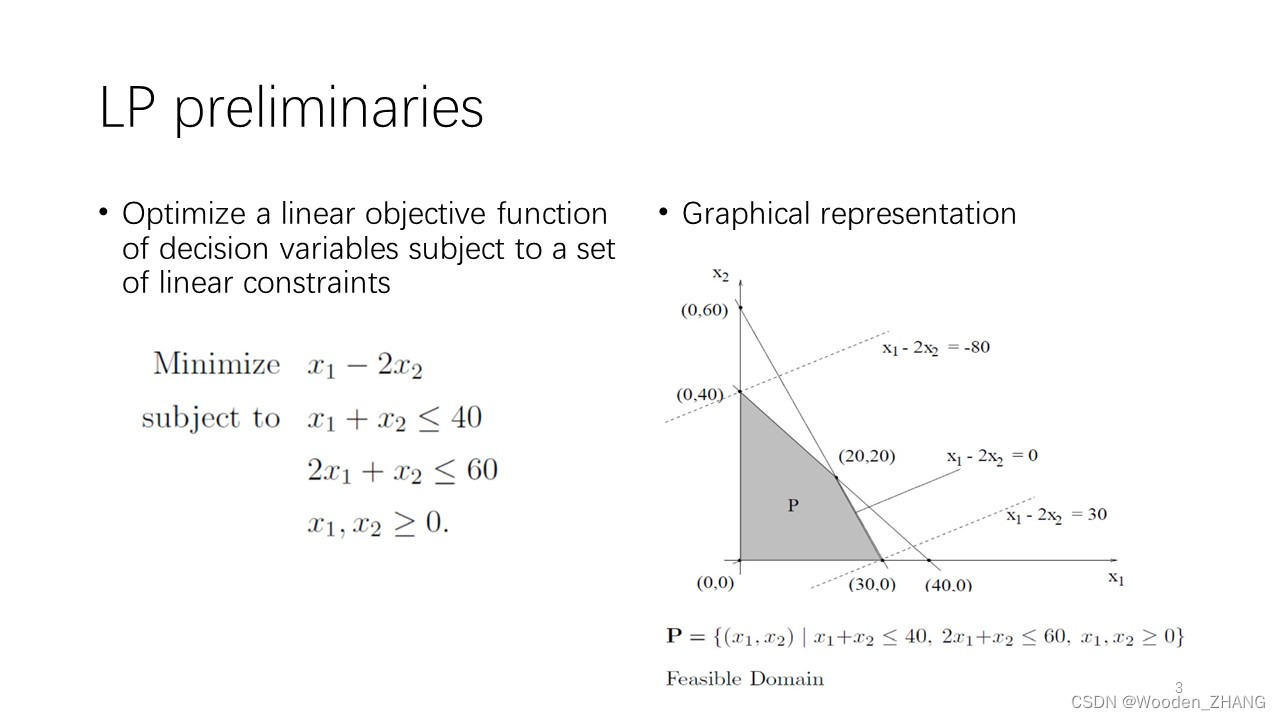
•LP preliminaries

•LP history

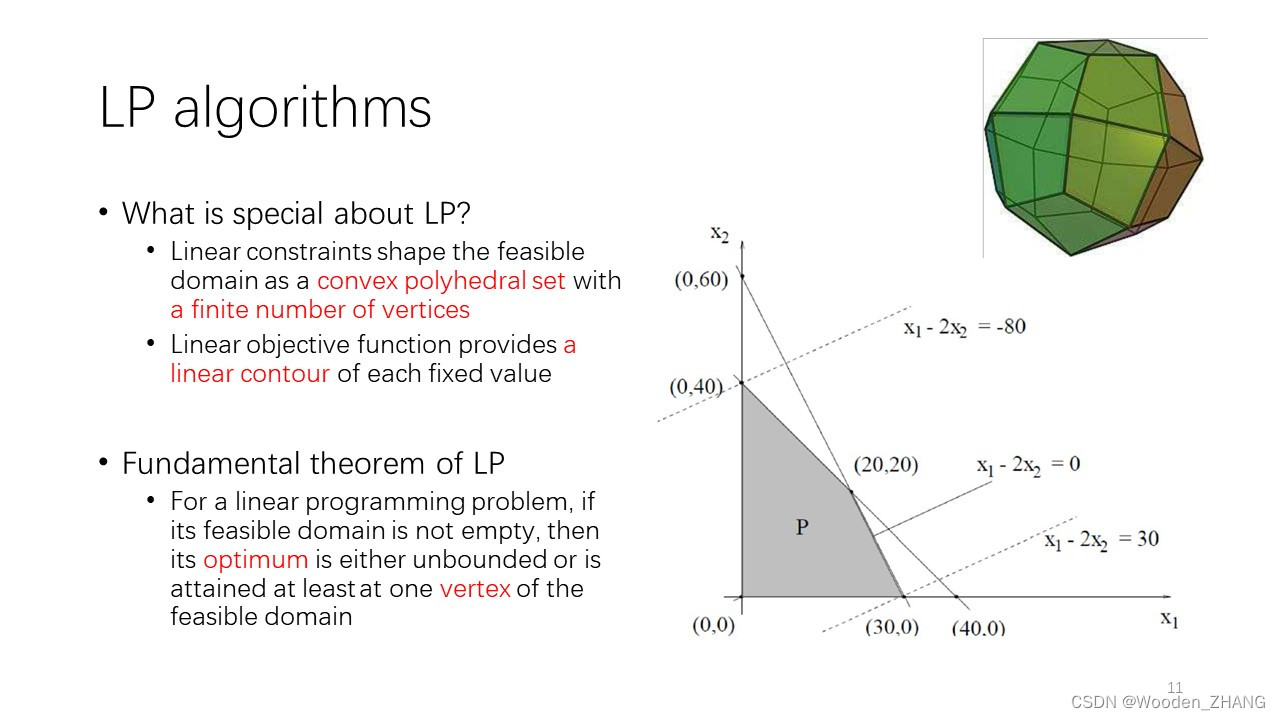
•LP algorithms

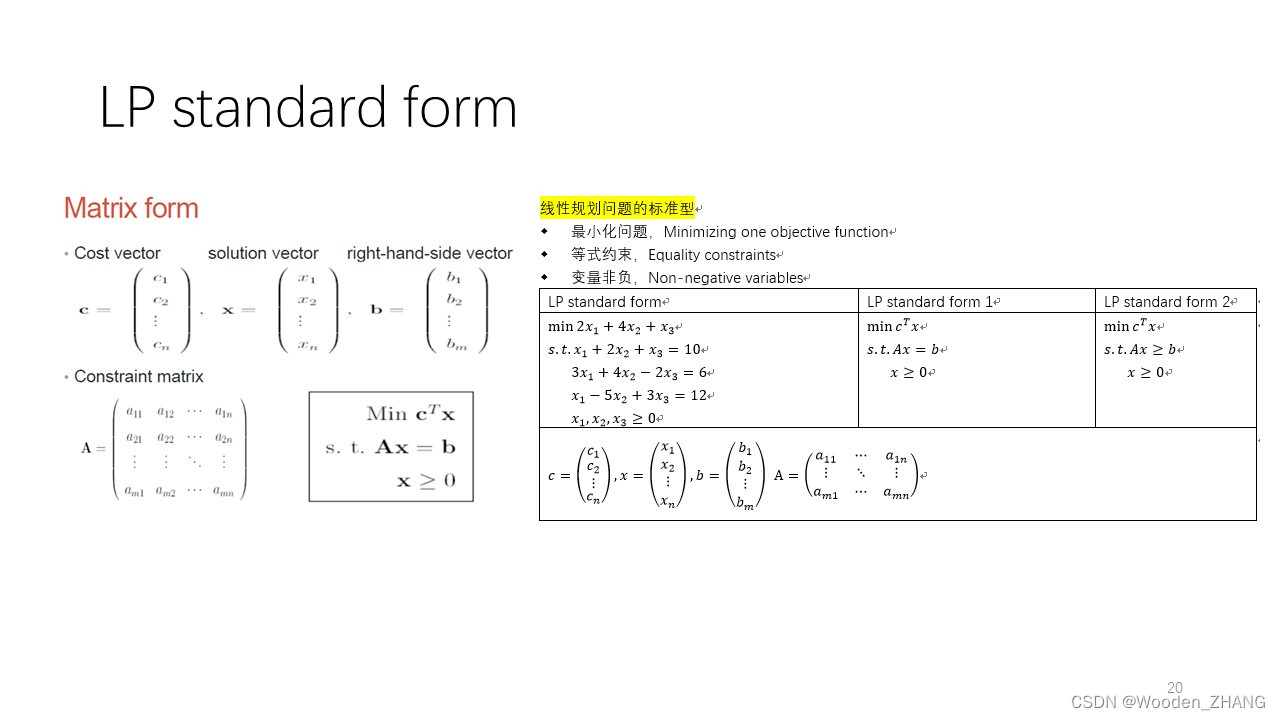
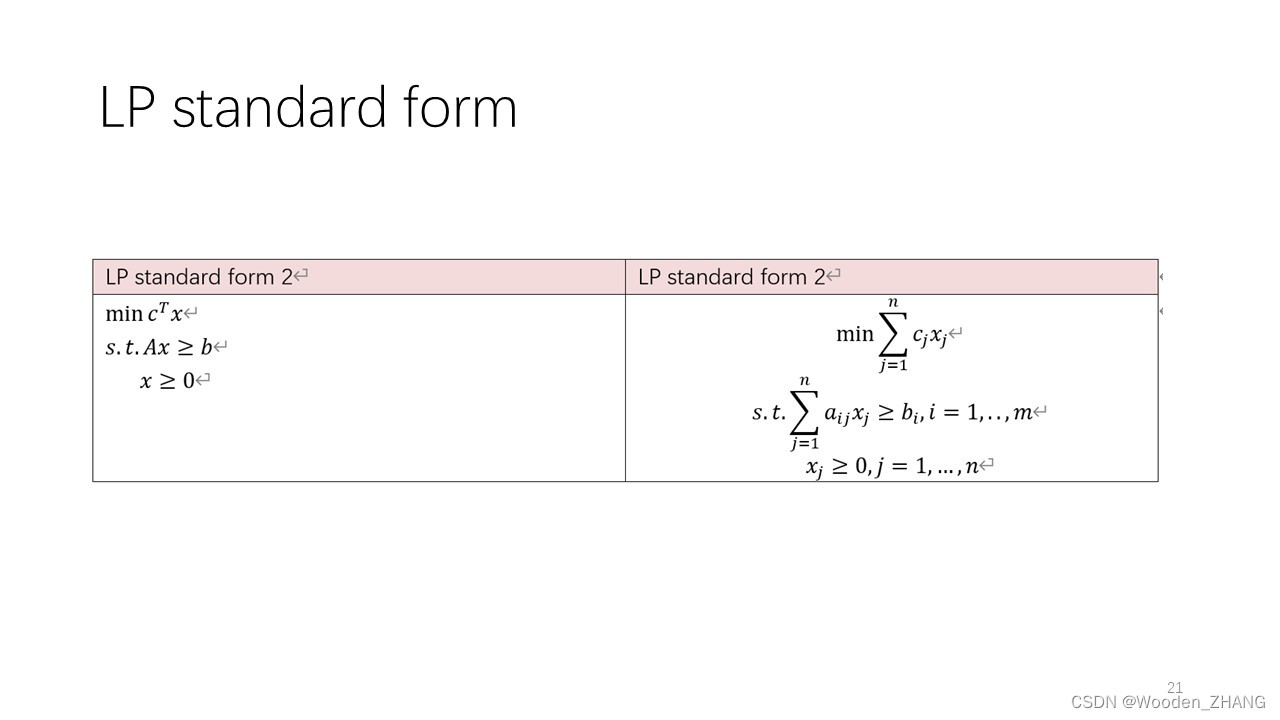
•LPstandard form

---------------------------------------

•LP是优化中最基础的内容，后续的高级内容都需要用到LP的知识。•Non-linear programming (NLP), network flows, integer programming (IP) 难度上差不多在一个层次。 •Conic programming (CP), semi-definite programming (SDP), robust programming难度上再高一个层次，涉及到从vector到matrix的转变。•变量的复杂度是从scalar(标量)--vector(向量)--matrix(矩阵)--tensor(张量)

---------------------------------------

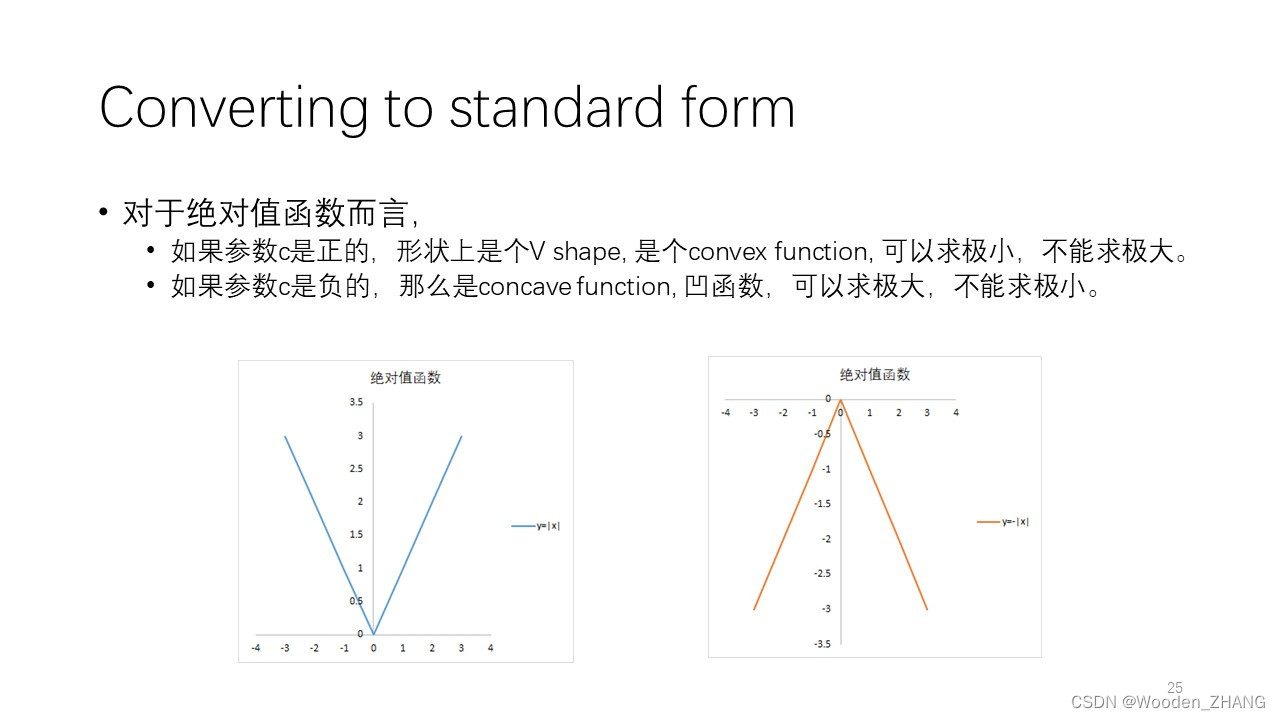
•LP的分析涉及到很多几何分析的概念，是建立在凸分析的基础上的。•比如，LP的求解方法主要是单纯形法(Simplex Method)与内点法(InteriorPoint Method)。•单纯形法是沿着可行域(多边形或者多面体)的边移动，从一个顶点移动到另外一个顶点。而内点法则是在可行域内部移动，不是在边界上移动。•这些都需要我们有几何上的直观概念。

-------------------------------------------

•Geometric intuition •几何直观，能够起到一个guiding principle的作用，让我们对问题有直观的认识，并在此基础上做一些speculation

•Algebraic manipulation •代数运算，是用来精确描述、证明几何上推测的过程，是系统性的求解过程，可重复，有理论支撑，涉及到很多算法和定理

•Computer programming•用计算机来求解问题，一般都是些iterative algorithm framework, 不用再手动去算

---------------------------------------------