分析rgb和yuv文件的通道概率分布和熵的计算--数据压缩部分实验

最新推荐文章于 2022-03-13 17:29:03 发布

文刀赤赤子！

最新推荐文章于 2022-03-13 17:29:03 发布

阅读量291

点赞数 1

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/sendhoh/article/details/114527599

本文档详细介绍了对RGB和YUV文件进行概率分布和熵计算的实验过程。实验者首先使用C++实现了读取RGB文件，计算各通道概率分布和熵的算法，并将结果输出到文本文件。接着，根据YUV4:2:0采样空间的特点，调整代码以处理YUV文件。实验结果显示了RGB和YUV各通道的熵值，整个过程体现了对图像编码和信息熵计算的理解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

作者：赤赤子

实验要求

对down.rgb和down.yuv分析三个通道的概率分布，并计算各自的熵。（编程实现）两个文件的分辨率均为256*256，yuv为4:2:0采样空间，存储格式为：rgb文件按每个像素BGR分量依次存放；YUV格式按照全部像素的Y数据块、U数据块和V数据块依次存放。

实验RGB

储备知识

1.rgb：采用这种编码方法，每种颜色都可用三个变量来表示，红色绿色以及蓝色的强度。记录及显示彩色图像时，rgb是最常见的一种方案。
2.信息熵的计算公式如下：

实验思路以及实现

RGB的思路

鉴于本人语言功底薄弱，所以还是用基础的c艹来实现这个实验。大体思路如下：
将RGB数据从RGB文件中读出，并分别保存到3个数组中，期间计算数据的概率分布和熵，并将这些数据打印到屏幕上即可。
具体思路：
1.首先使用fopen函数打开rgb文件。
fopen函数的用法如下：这里参见另一位博主的文章啦 link！点这里看c艹基本函数用法！.
2.通过fseek函数，先找到文件的末尾，再计算出文件中数据的总大小。
（正常来说应该这么做，不过这个实验是针对特定的已知大小的图片的已在要求内给出，所以其实只需要直接规定数组的长度就可以啦！）
3.将RGB文件中的数据读入一个大数组中，这个大数组的长度就是已知，而由于RGB文件中的排列是B，G，R的顺序，所以我们便可以用循环的方法来得出存储R，G，B相应数据的长度的数组。
这里也就是说RGB文件的顺序上面稍稍需要留心！
4.得出了这样的数组，就可以分别计算其概率分布和信息熵了。
5.最后，利用printf输出RGB的概率分布和熵就~~大功告成~~完成一半了！
纠错：需要三个text文件分别写入RGB的概率分布，直接输出会很混乱。

RGB的实验过程（思路实现）

1.读取文件

FILE* fp = fopen("C:\\Users\\27202\\Desktop\\down.rgb", "rb");   
//地址放在了c盘，这里人各有异

2.创建写入的text文件

   FILE* fp1 = fopen("C:\\Users\\27202\\Desktop\\R.txt", "w");
   FILE* fp2 = fopen("C:\\Users\\27202\\Desktop\\G.txt", "w");
   FILE* fp3 = fopen("C:\\Users\\27202\\Desktop\\B.txt", "w");

3.创建变量及数组（所需要的）

    int h=256;
	int w=256; //这里是长和宽的像素情况
	int i=0;
	int j=0; //这里是循环变量的设定
	unsigned char r[65536];
    unsigned char g[65536];
    unsigned char b[65536]; //这里的数组是256*256的像素数
    unsigned char buffer[196608]; //这是read出来的buffer数组包含RGB三个量的全部
	double frequency_r[256] = { 0 };
    double frequency_g[256] = { 0 };
    double frequency_b[256] = { 0 }; //这里的数组用来存放通道的概率
	double Entropy_r=0;
	double Entropy_g=0;
	double Entropy_b=0; //知识点：entropy是熵的意思
	//这里出现了bug我由于一开始忘记了初始化，再找回来用了很长时间

~~我要是再忘记初始化我就是傻狗。~~

4.循环体的构建
(1).我们先把fp文件读到buffer数组里面

    fread(buffer, 1, 196608, fp);

(2).按照特殊的对应方式将r，g，b分别对应到读出来的buffer的位置上

    for (i=0,j=0;i<w*h*3;i=i+3,j++){
		b[j]= *(buffer+i);
        g[j]= *(buffer+i+1);
        r[j]= *(buffer+i+2);}

(3).计算概率

for（i=0;i<256; i++)
   {for (j=0;j<w*h; j++)
      {if(int(r[j]) == i) {frequency_r[i]++;}
       if(int(g[j]) == i) { frequency_g[i]++; }
       if(int(b[j])==i) {frequency_b[i]++;}
      }
   }
   for (int i = 0; i < 256; i++)
   {frequency_r[i] = frequency_r[i] /double(w * h);
    frequency_g[i] = frequency_g[i] /double(w * h);
    frequency_b[i] = frequency_b[i] /double(w * h);
   }

(4).计算熵并输出

   for (int i = 0; i < 256; i++)
	{
		if (frequency_r[i]!= 0)
		{Entropy_r+=(-1)*frequency_r[i]*(log(frequency_r[i])/log(2.0));} 
		if (frequency_b[i]!= 0)
		{Entropy_b+=(-1)*frequency_b[i]*(log(frequency_b[i])/log(2.0));}
		if (frequency_g[i]!= 0)
		{Entropy_g+=(-1)*frequency_g[i]*(log(frequency_g[i])/log(2.0));}
	} 
	//注意这里除号上下的类型需要保持一致，所以2要写成2.0
	cout<<"entropy of red is"<<Entropy_r<<endl;
	cout<<"entropy of green is"<<Entropy_g<<endl;
	cout<<"entropy of blue is"<<Entropy_b<<endl;

(5).将概率写入文件并将文件关闭

   fprintf(fp1, "Symbol\tFrequency\n");
   fprintf(fp2, "Symbol\tFrequency\n");
   fprintf(fp3, "Symbol\tFrequency\n");
   for (int i = 0; i < 256; i++)
   {
      fprintf(fp1, "%-3d\t%-8f\n", i, frequency_r[i]);
      fprintf(fp2, "%-3d\t%-8f\n", i, frequency_g[i]); 
      fprintf(fp3, "%-3d\t%-8f\n", i, frequency_b[i]); 
   }//这里是规定了位数以及规范的格式，输出更加美观
   fclose(fp);
   fclose(fp1);
   fclose(fp2);
   fclose(fp3);//关闭文件

完整代码段

#include<iostream>
#include<math.h>
#include<stdio.h>
using namespace std;
int main(){
	FILE* fp = fopen("C:\\Users\\27202\\Desktop\\down.rgb", "rb");   
   FILE* fp1 = fopen("C:\\Users\\27202\\Desktop\\R.txt", "w");
   FILE* fp2 = fopen("C:\\Users\\27202\\Desktop\\G.txt", "w");
   FILE* fp3 = fopen("C:\\Users\\27202\\Desktop\\B.txt", "w");
     int h=256;
	int w=256;
	int i=0;
	int j=0; 
	unsigned char r[65536];
    unsigned char g[65536];
    unsigned char b[65536]; 
    unsigned char buffer[196608]; 
	double frequency_r[256] = { 0 };
    double frequency_g[256] = { 0 };
    double frequency_b[256] = { 0 }; 
	long double Entropy_r=0;
	long double Entropy_g=0;
	long double Entropy_b=0; 
	  fread(buffer, 1, 196608, fp);
	      for (i=0,j=0;i<w*h*3;i=i+3,j++){
		b[j]= *(buffer+i);
        g[j]= *(buffer+i+1);
        r[j]= *(buffer+i+2);}
		  for (i=0;i<256;i++)
   {for (int j = 0; j < w * h; j++)
      {if(int(r[j]) == i) {frequency_r[i]++;}
       if(int(g[j]) == i) { frequency_g[i]++; }
       if(int(b[j])==i) {frequency_b[i]++;}
      }
   }
   for (int i = 0; i < 256; i++)
   {frequency_r[i] = frequency_r[i] /double(w * h);
    frequency_g[i] = frequency_g[i] /double(w * h);
    frequency_b[i] = frequency_b[i] /double(w * h);
   }

   fprintf(fp1, "Symbol\tFrequency\n");
   fprintf(fp2, "Symbol\tFrequency\n");
   fprintf(fp3, "Symbol\tFrequency\n");
   for (int i = 0; i < 256; i++)
   {
      fprintf(fp1, "%-3d\t%-8f\n", i, frequency_r[i]);
      fprintf(fp2, "%-3d\t%-8f\n", i, frequency_g[i]); 
      fprintf(fp3, "%-3d\t%-8f\n", i, frequency_b[i]); 
   }
    for (int i = 0; i < 256; i++)
	{
		if (frequency_r[i]!= 0)
		{Entropy_r+=(-1)*frequency_r[i]*(log(frequency_r[i])/log(2.0));} 
		if (frequency_b[i]!= 0)
		{Entropy_b+=(-1)*frequency_b[i]*(log(frequency_b[i])/log(2.0));}
		if (frequency_g[i]!= 0)
		{Entropy_g+=(-1)*frequency_g[i]*(log(frequency_g[i])/log(2.0));}
	} 
	cout<<"entropy of red is    "<<Entropy_r<<endl;
	cout<<"entropy of green is  "<<Entropy_g<<endl;
	cout<<"entropy of blue is   "<<Entropy_b<<endl;
   fclose(fp);
   fclose(fp1);
   fclose(fp2);
   fclose(fp3);
   return 0;}

实验结果以及其截图

cmd执行结果
txt结果如下：
用画图拼的图真的好用！

实验YUV

储备知识

1.yuv：得到rgb后再经过矩阵变换电路得到亮度信号y和两个色差信号b-y（即u）、r-y（即v）最后发送端将亮度和色差三个信号分别进行编码，用同一信道发送出去。这种色彩的表示方法就是所谓的yuv色彩空间表示。.Y 表示亮度(luma)，CbCr 表示色度(chroma）。
2.我觉得可以参考RGB的方法快速完成。
3.通常对 yuv444，yuv422，yuv420 的解释是后面三个数字分别对应前面三个字母。拿 yuv422 来说，y 对应 4，表示四个图形像素中，每个都有亮度值；u 对应 2，表示四个图形像素中，Cb 只占用两个像素；v 对应 2，表示四个图形像素中， Cr 占用两个像素。而420比较特殊，我们通过一张图片来说明：
辛苦从知乎找来的！
图来源于 Chrominance Subsampling in Digital Images（侵权删除哦）~~（伪装大佬）~~
在这个实验中420只是说明4：2：0 水平方向是1/2，垂直方向是1/2，表示一个色度像素对应了四个图形像素。
4.分析之后我们可以得到：视频帧的宽和高分别为w和h，那么一帧YUV420像素数据占用其中前w×h存储Y，接着的wh1/4存储U，最后wh1/4 存储V。也就是大小为1.5wh哦。

在给出的图片格式条件下，可以这么看：
YUV数据的0~65535字节是Y分量值；65536～81919字节是U分量；81920～98303字节是V分量。

实验思路及实现

唉说实话我就觉得pathon会简单很多很多，但是作为一个~~小废物~~（bushi）我实在忘了语法。我最开始也想用matlab来做来着，奈何我也不会写，试了试算了吧。哦想法多么的美好，最后还是铁打的c艹。

YUV的思路

其实这个编程可基于RGB变成稍作改动，同样是读取数据，区别在于YUV读入的数组规模要比图像尺寸256*256略大。

RGB的实验过程（思路实现）

这里只给出需要修改的步骤。
1.读取文件

FILE* fp = fopen("C:\\Users\\27202\\Desktop\\down.yuv", "rb");

2设定数组（初始化）

	unsigned char y[65536];//256*256
    unsigned char u[16384];
    unsigned char v[16384]; //U和V的大小是图形像素数除以4
    unsigned char buffer[98304]; //总数据数（即相加）

3.读取数据以及y,u,v在buffer中的对应关系为

fread(buffer, 1, 98304, fp);
	for (i=0;i<w*h;i=i++){
		y[i]= buffer[i];}
	for (i=65536,j=0;i<81920;j=j++,i=i++){
		u[j]=buffer[i];}
	for (i=81920,j=0;i<98304;j=j++,i=i++){
		v[j]=buffer[i];}

4.概率的计算

 for (i=0;i<256;i++)
   {for (int j = 0; j < w * h; j++)
      if(int(y[j])==i) {frequency_y[i]++;}
     }
  for (i=0;i<256;i++)
   {for (int j = 0; j < w * h/4; j++)
      {if(int(u[j])==i) {frequency_u[i]++;}
      }
   }
    for (i=0;i<256;i++)
   {for (int j = 0; j < w * h/4; j++)
      {if(int(v[j])==i) {frequency_v[i]++;}
      }
   }
   for (int i = 0; i < 256; i++)
   {frequency_y[i] = frequency_y[i] /65536;
    frequency_u[i] = frequency_u[i] /16384;
    frequency_v[i] = frequency_v[i] /16384;//注意这里的概率要对应相应字节数的大小
   }

剩余部分思路完全一致，故不给出说明。

完整代码段

#include<iostream>
#include<math.h>
#include<stdio.h>
using namespace std;
int main(){
	FILE* fp = fopen("C:\\Users\\27202\\Desktop\\down.yuv", "rb");   
    FILE* fp1 = fopen("C:\\Users\\27202\\Desktop\\Y.txt", "w");
    FILE* fp2 = fopen("C:\\Users\\27202\\Desktop\\U.txt", "w");
    FILE* fp3 = fopen("C:\\Users\\27202\\Desktop\\V.txt", "w");
    int h=256;
	int w=256;
	int i=0;
	int j=0; 
	unsigned char y[65536];
    unsigned char u[16384];
    unsigned char v[16384]; 
    unsigned char buffer[98304]; 
	double frequency_y[256] = { 0 };
    double frequency_u[256] = { 0 };
    double frequency_v[256] = { 0 }; 
	long double Entropy_y=0;
	long double Entropy_u=0;
	long double Entropy_v=0; 
	fread(buffer, 1, 98304, fp);
	for (i=0;i<w*h;i=i++){
		y[i]= buffer[i];}
	for (i=65536,j=0;i<81920;j=j++,i=i++){
		u[j]=buffer[i];}
	for (i=81920,j=0;i<98304;j=j++,i=i++){
		v[j]=buffer[i];}
  for (i=0;i<256;i++)
   {for (int j = 0; j < w * h; j++)
      if(int(y[j])==i) {frequency_y[i]++;}
      
   }
  for (i=0;i<256;i++)
   {for (int j = 0; j < w * h/4; j++)
      {if(int(u[j])==i) {frequency_u[i]++;}
      }
   }
    for (i=0;i<256;i++)
   {for (int j = 0; j < w * h/4; j++)
      {if(int(v[j])==i) {frequency_v[i]++;}
      }
   }
   for (int i = 0; i < 256; i++)
   {frequency_y[i] = frequency_y[i] /65536;
    frequency_u[i] = frequency_u[i] /16384;
    frequency_v[i] = frequency_v[i] /16384;
   }
   fprintf(fp1, "Symbol\tFrequency\n");
   fprintf(fp2, "Symbol\tFrequency\n");
   fprintf(fp3, "Symbol\tFrequency\n");
   for (int i = 0; i < 256; i++)
   {
      fprintf(fp1, "%-3d\t%-8f\n", i, frequency_y[i]);
      fprintf(fp2, "%-3d\t%-8f\n", i, frequency_u[i]); 
      fprintf(fp3, "%-3d\t%-8f\n", i, frequency_v[i]); 
   }
    for (int i = 0; i < 256; i++)
	{
		if (frequency_y[i]!= 0)
		{Entropy_y+=(-1)*frequency_y[i]*(log(frequency_y[i])/log(2.0));} 
		if (frequency_u[i]!= 0)
		{Entropy_u+=(-1)*frequency_u[i]*(log(frequency_u[i])/log(2.0));}
		if (frequency_v[i]!= 0)
		{Entropy_v+=(-1)*frequency_v[i]*(log(frequency_v[i])/log(2.0));}
	} 
	cout<<"entropy of y is    "<<Entropy_y<<endl;
	cout<<"entropy of u is    "<<Entropy_u<<endl;
	cout<<"entropy of v is    "<<Entropy_v<<endl;
   fclose(fp);
   fclose(fp1);
   fclose(fp2);
   fclose(fp3);
   return 0;}

实验结果及其截图

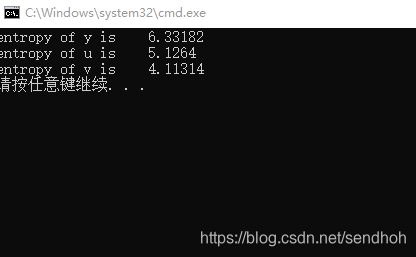
cmd执行结果
txt结果如下：画图拼成的txt结果

总结

其实这次的实验没费多大的事，就是一个读文件加计算的操作，不过既然作为子赫第一次写这个csdn，写博客的时间绝对占用了做实验时间的五倍以上，希望以后能帮到某个陌生人吧（但感觉太简单了也没人会需要）。
在做实验的过程中YUV那个设定数组的时候不小心把v也打成了u，导致后来的v模块的熵一直为零，我反反复复的找问题，浪费了很多时间和心情，而且debug还找不出来，心力憔悴了一小会。不过后来还是发现了，庆幸自己没放弃。
其实我的编程基础很薄弱，有一些知识点早就忘了，但也没借鉴谁的思路，坚持让自己只能百度语法一直到最后，这份心情也值得纪念，毕竟，也好久没有用心的自己做好一件事情了。
子赫加油。
并且有很多大佬用pathon给搞出图形来了，看着也挺羡慕的，也要记住这份遗憾的心情。