二叉树的经典例题、还原二叉树（一）

题目如下：

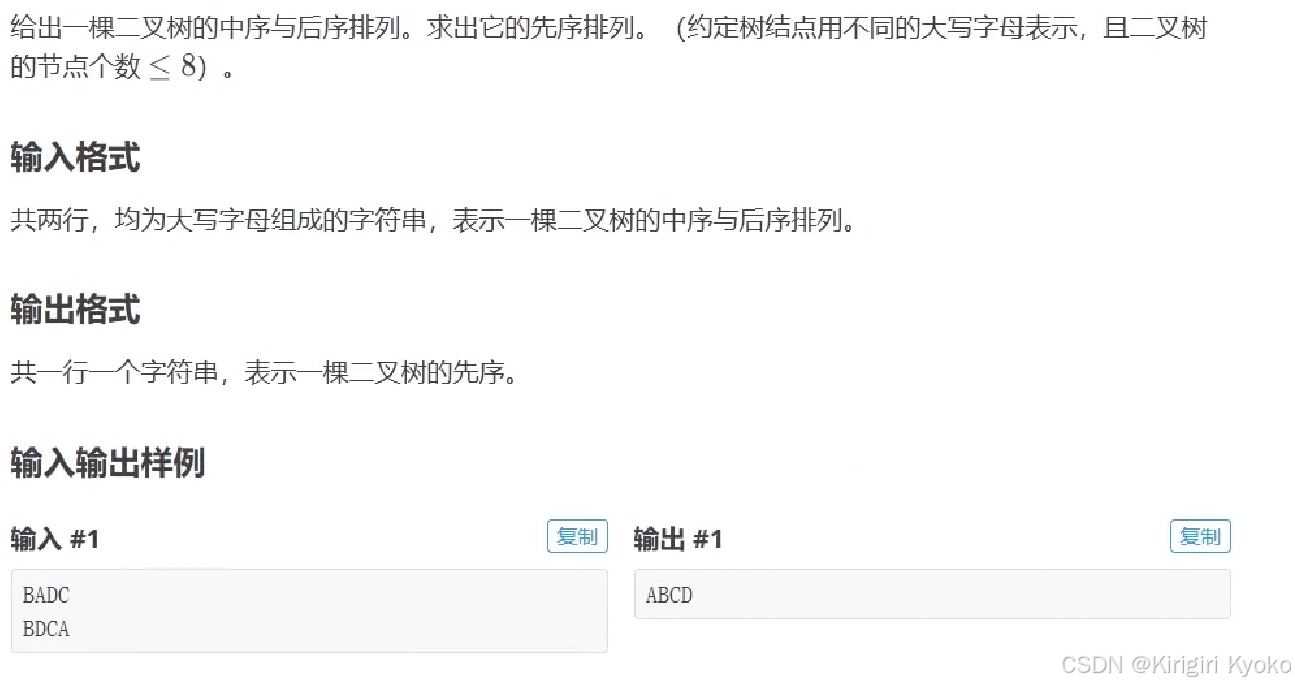
        首先说一下这类题的解法：1、先确定根节点   2、根据根节点，划分出左右子树。那么如何确定根节点呢？我们知道，后序遍历是先遍历左右子树，最后遍历根节点。那么我们可以根据后序遍历的最后一个元素，确定出整颗二叉树的根节点（在本例题中，根节点为A）。找到根节点A之后，我们再回到中序遍历上，此时A就划分出了左右两颗子树（在本例题中，左子树为B，右子树为DC）。然后接着重复上述解法，因此，我们可以用递归来解决。

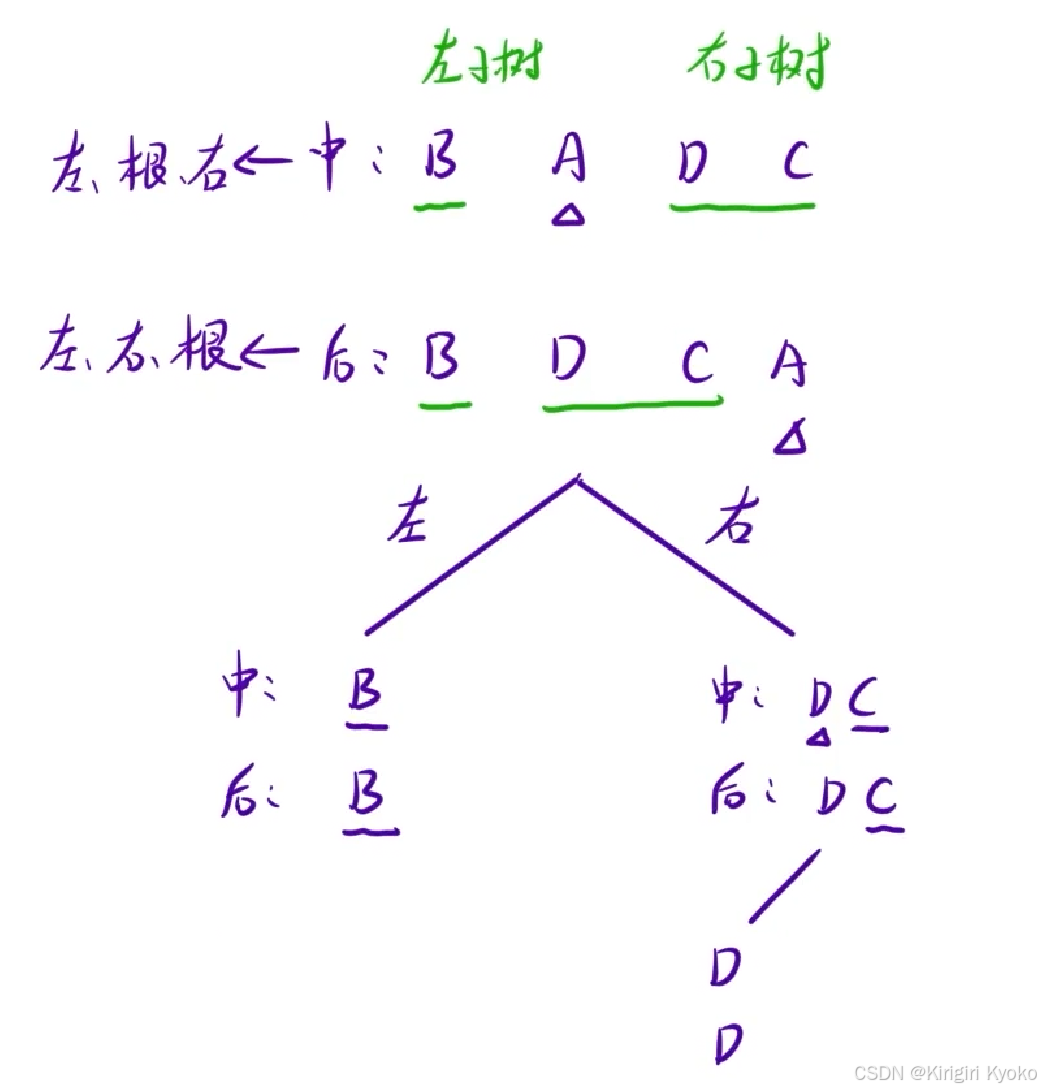
        既然已经知道了要用递归来实现，那么该如何编写这个递归函数（函数名dfs）呢？由上面分析，首先我们可以确定该函数返回值为void，问题就是函数里的参数该怎么写。题目是要先输入两个字符串的 ，当递归到左右子树的时候，我们是相当于拿出了字符串的一部分。因此在传参的时候，我们只需要传入要处理的那一段字符串即可。因此我们定义四个变量：L1标记中序遍历的左端点，L2标记后序遍历的左端点，r1标记中序遍历的右端点，r2标记后序遍历的右端点。在函数体内部，我们还需要定义一个变量p，用来标记中序遍历中根节点的位置。

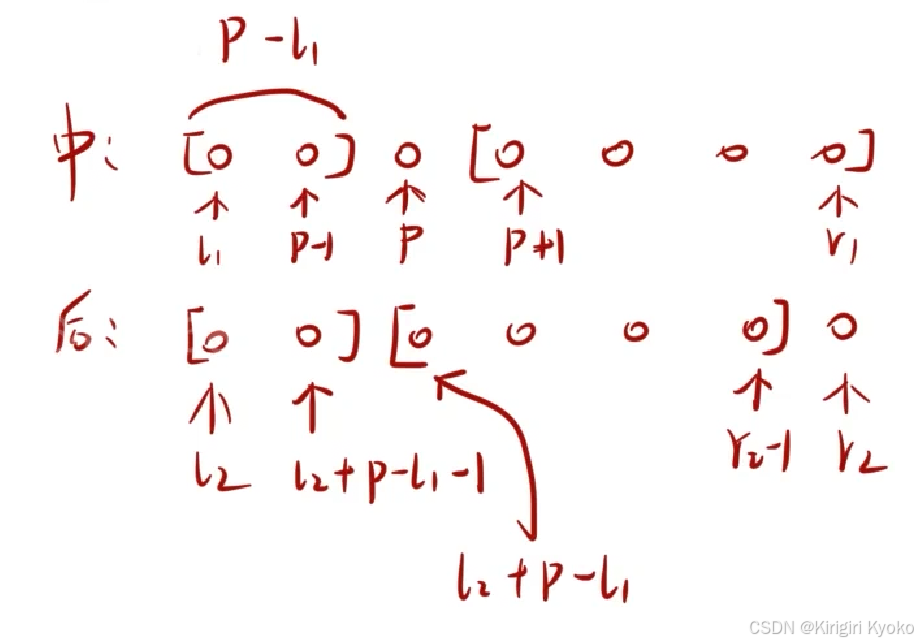
 代码如下：

#include <iostream>
using namespace std;

string s1, s2;

void dfs(int l1, r1, l2, r2)
{
	if(l1 > r1)
	{
		return;		
	}
		
	cout << s2[r2];
	
	int p = l1;
	while(s1[p] != s2[r2])
	{
		p++;		
	}
	
	dfs(l1, p - 1, l2, l2 + p - l1 - 1);
	dfs(p + 1, r1, l2 + p - l1, r2 - 1);
	
}

int main()
{
	cin >> s1 >> s2;
	
	dfs(0, s1.size() - 1, 0, s2.size() - 1);
	
	return 0;
}