基本信息
本赛季由 sunchaoyi \color{purple}\texttt{sunchaoyi} sunchaoyi, jr_zlw \color{orange}\texttt{jr\_zlw} jr_zlw, Skyzhou \color{purple}\texttt{Skyzhou} Skyzhou 组队,全靠大佬带飞~。
中文队名:正在验证该队是否是真人。
英文队名:Verifying we are human.
- 队友 Sky 的记录!被带飞!!!
训练情况总览
| Id \texttt{Id} Id | Date \texttt{Date} Date | Title \texttt{Title} Title | Solved \texttt{Solved} Solved | Dirt \texttt{Dirt} Dirt | Post-contest Solved \texttt{Post-contest Solved} Post-contest Solved |
|---|---|---|---|---|---|
| 1 1 1 | 2025.05.02 2025.05.02 2025.05.02 | The 2023 Guangdong Provincial Collegiate Programming Contest | 8 / 13 8/13 8/13 | 55 % 55\% 55% | 10 / 13 10/13 10/13 |
| 2 2 2 | 2025.05.15 2025.05.15 2025.05.15 | The 2024 ICPC Asia Hangzhou Regional Contest | 6 / 13 6/13 6/13 | 62 % 62\% 62% | 6 / 13 6/13 6/13 |
| 3 3 3 | 2025.05.19 2025.05.19 2025.05.19 | The 2025 ICPC Wuhan Invitational Contest | 5 / 13 5/13 5/13 | 69 % 69\% 69% | 7 / 13 7/13 7/13 |
| 4 4 4 | 2025.05.21 2025.05.21 2025.05.21 | The 2025 ICPC China Zhejiang Province Programming Contest | 6 / 13 6/13 6/13 | 76 % 76\% 76% | 7 / 13 7/13 7/13 |
| 5 5 5 | 2025.05.22 2025.05.22 2025.05.22 | The 2024 ICPC Asia Shanghai Regional Contest | 5 / 13 5/13 5/13 | 73 % 73\% 73% | 7 / 13 7/13 7/13 |
| 6 6 6 | 2025.05.25 2025.05.25 2025.05.25 | The 2024 CCPC Jinan Site | 4 / 13 4/13 4/13 | 50 % 50\% 50% | 7 / 13 7/13 7/13 |
| 7 7 7 | 2025.05.26 2025.05.26 2025.05.26 | The 2024 ICPC Southeastern Europe Regional Contest | 7 / 13 7/13 7/13 | 41 % 41\% 41% | 8 / 13 8/13 8/13 |
| 8 8 8 | 2025.05.27 2025.05.27 2025.05.27 | The 2024 ICPC Central Europe Regional Contest | 5 / 12 5/12 5/12 | 28 % 28\% 28% | 6 / 12 6/12 6/12 |
| 9 9 9 | 2025.05.29 2025.05.29 2025.05.29 | The 2023 ICPC Asia Jinan Regional Contest | 6 / 13 6/13 6/13 | 14 % 14\% 14% | 7 / 13 7/13 7/13 |
| 10 10 10 | 2025.05.30 2025.05.30 2025.05.30 | The 2023 CCPC Guilin Site | 4 / 13 4/13 4/13 | 60 % 60\% 60% | 7 / 13 7/13 7/13 |
| 11 11 11 | 2025.06.02 2025.06.02 2025.06.02 | The 2025 Guangdong Provincial Collegiate Programming Contest | 5 / 13 5/13 5/13 | 62 % 62\% 62% | 8 / 13 8/13 8/13 |
| 12 12 12 | 2025.07.15 2025.07.15 2025.07.15 | 2025牛客暑期多校训练营1 | 4 / 12 4/12 4/12 | 33 % 33\% 33% | 6 / 12 6/12 6/12 |
| 13 13 13 | 2025.07.17 2025.07.17 2025.07.17 | 2025牛客暑期多校训练营2 | 7 / 13 7/13 7/13 | 59 % 59\% 59% | 7 / 13 7/13 7/13 |
| 14 14 14 | 2025.07.22 2025.07.22 2025.07.22 | 2025牛客暑期多校训练营3 | 7 / 13 7/13 7/13 | 42 % 42\% 42% | 7 / 13 7/13 7/13 |
| 15 15 15 | 2025.07.24 2025.07.24 2025.07.24 | 2025牛客暑期多校训练营4 | 4 / 13 4/13 4/13 | 50 % 50\% 50% | 8 / 13 8/13 8/13 |
| 16 16 16 | 2025.07.29 2025.07.29 2025.07.29 | 2025牛客暑期多校训练营5 | 4 / 13 4/13 4/13 | 43 % 43\% 43% | 6 / 13 6/13 6/13 |
| 17 17 17 | 2025.07.31 2025.07.31 2025.07.31 | 2025牛客暑期多校训练营6 | 5 / 13 5/13 5/13 | 29 % 29\% 29% | 8 / 13 8/13 8/13 |
| 18 18 18 | 2025.08.05 2025.08.05 2025.08.05 | 2025牛客暑期多校训练营7 | 5 / 10 5/10 5/10 | 64 % 64\% 64% | 5 / 10 5/10 5/10 |
| 19 19 19 | 2025.08.07 2025.08.07 2025.08.07 | 2025牛客暑期多校训练营8 | 5 / 11 5/11 5/11 | 38 % 38\% 38% | 6 / 11 6/11 6/11 |
| 20 20 20 | 2025.08.12 2025.08.12 2025.08.12 | 2025牛客暑期多校训练营9 | 5 / 13 5/13 5/13 | 55 % 55\% 55% | 6 / 12 6/12 6/12 |
| 21 21 21 | 2025.08.14 2025.08.14 2025.08.14 | 2025牛客暑期多校训练营10 | 5 / 12 5/12 5/12 | 38 % 38\% 38% | 7 / 12 7/12 7/12 |
| 22 22 22 | 2025.08.30 2025.08.30 2025.08.30 | The 2023 CCPC Harbin Site | 6 / 13 6/13 6/13 | 33 % 33\% 33% | 6 / 13 6/13 6/13 |
| 23 23 23 | 2025.08.31 2025.08.31 2025.08.31 | The 2023 CCPC Qinghuangdao Site | 5 / 13 5/13 5/13 | 44 % 44\% 44% | 6 / 13 6/13 6/13 |
| 24 24 24 | 2025.09.05 2025.09.05 2025.09.05 | The 15th Shandong Provincial Collegiate Programming Contest | 7 / 13 7/13 7/13 | 50 % 50\% 50% | 7 / 13 7/13 7/13 |
| 25 25 25 | 2025.09.07 2025.09.07 2025.09.07 | The 2025 ICPC Asia East Continent Online Contest (I) | 6 / 13 6/13 6/13 | 14 % 14\% 14% | 8 / 13 8/13 8/13 |
| 26 26 26 | 2025.09.14 2025.09.14 2025.09.14 | The 2025 ICPC Asia East Continent Online Contest (II) | 4 / 12 4/12 4/12 | 33 % 33\% 33% | 8 / 12 8/12 8/12 |
| 27 27 27 | 2025.09.20 2025.09.20 2025.09.20 | The 2025 CCPC Online Contest | 6 / 13 6/13 6/13 | 45 % 45\% 45% | 8 / 13 8/13 8/13 |
| 28 28 28 | 2025.09.11 2025.09.11 2025.09.11 | The 2023 ICPC Asia Hefei Regional Contest | 4 / 12 4/12 4/12 | 71 % 71\% 71% | 5 / 12 5/12 5/12 |
| 29 29 29 | 2025.09.25 2025.09.25 2025.09.25 | The 2021 ICPC Southeastern European Regional Programming Contest | 8 / 14 8/14 8/14 | 42 % 42\% 42% | 9 / 14 9/14 9/14 |
| 30 30 30 | 2025.10.02 2025.10.02 2025.10.02 | The 2022 ICPC Asia Hong Kong Regional Contest | 6 / 12 6/12 6/12 | 57 % 57\% 57% | 9 / 12 9/12 9/12 |
| 31 31 31 | 2025.10.09 2025.10.09 2025.10.09 | The 2024 ICPC Asia Hong Kong Regional Contest | 5 / 13 5/13 5/13 | 54 % 54\% 54% | 6 / 13 6/13 6/13 |
| 32 32 32 | 2025.10.13 2025.10.13 2025.10.13 | The 2018 ICPC Asia Qingdao Regional Contest | 7 / 13 7/13 7/13 | 12 % 12\% 12% | 8 / 13 8/13 8/13 |
| 33 33 33 | 2025.10.17 2025.10.17 2025.10.17 | The 2024 ICPC Asia Shenyang Regional Contest | 3 / 13 3/13 3/13 | 50 % 50\% 50% | 6 / 13 6/13 6/13 |
| 34 34 34 | 2025.10.19 2025.10.19 2025.10.19 | The 2024 Shandong Provincial Collegiate Programming Contest | 8 / 13 8/13 8/13 | 38 % 38\% 38% | 9 / 13 9/13 9/13 |
| 35 35 35 | 2025.10.23 2025.10.23 2025.10.23 | The 2025 ICPC Asia Xi’an Regional Contest | 5 / 13 5/13 5/13 | 44 % 44\% 44% | 8 / 13 8/13 8/13 |
| 36 36 36 | 2025.10.26 2025.10.26 2025.10.26 | The 2025 ICPC Asia Chengdu Regional Contest | 6 / 13 6/13 6/13 | 33 % 33\% 33% | 9 / 13 9/13 9/13 |
| 37 37 37 | 2025.11.02 2025.11.02 2025.11.02 | The 2025 ICPC Asia Wuhan Regional Contest | 5 / 13 5/13 5/13 | 37 % 37\% 37% | 7 / 13 7/13 7/13 |
| 38 38 38 | 2025.11.05 2025.11.05 2025.11.05 | The 2022 ICPC Asia Nanjing Regional Contest | 7 / 13 7/13 7/13 | 46 % 46\% 46% | 7 / 13 7/13 7/13 |
| 39 39 39 | 2025.11.09 2025.11.09 2025.11.09 | The 2025 ICPC Asia Nanjing Regional Contest | 4 / 13 4/13 4/13 | 42 % 42\% 42% | 7 / 13 7/13 7/13 |
| 40 40 40 | 2025.11.23 2025.11.23 2025.11.23 | The 2025 ICPC Asia Shenyang Regional Contest | 4 / 13 4/13 4/13 | 33 % 33\% 33% | 7 / 13 7/13 7/13 |
| 41 41 41 | 2025.11.30 2025.11.30 2025.11.30 | The 2025 CCPC Chongqing Site | 4 / 13 4/13 4/13 | 20 % 20\% 20% | 4 / 13 4/13 4/13 |
训练记录
省赛备战
2025.05.02 The 2023 Guangdong Provincial Collegiate Programming Contest
备战省赛,也是组队后的第一次训练。
这一场签到题比较多,一小时以内按顺序过了 A,I,C,D,K。接下来我和 Sky 讨论了一下 M 的做法,确定了 O ( n 2 ) O(n^2) O(n2) 的 DP 维护直径,其间 Zlw 一眼 B 板子题,在 1.5h 一发通过了该题。
之后我和 Zlw 尝试口胡 E,F,没错他基本口胡出来了,大力模板。Sky 提交 M 题 RE,我去瞅了眼,发现三点共线导致分母为 0 0 0,立马帮他改成了叉积写法。之后又 WA,看了半天发现是 INF 开的不够大,红温……好在 3.5h 内通过。
然后我开始写 E 的字典树,写了半天发现巨丑还会运行错误,果断叫上 Zlw 来写,在提交了几发后发现神秘错误,在封榜后通过。之后就是 F,和队友确定了线段树二分写法,但是似乎和他的码风不太一样,于是被踹下来。但是由于写得有点屎,赛时没过,知道赛后 40 min 后通过该题。
最后赛时 8 8 8 题收尾(主要由 Zlw 写了一大半的题 orzorzorz,以及 Sky 的难题攻克)!
F 题有点深刻,自己又写了一遍。终于琢磨出为什么赛时会有这么多队伍过,原来还有两支 log \log log 的弱智写法。还是写一下线段树二分的做法吧,借鉴了一下题解,时间复杂度 O ( ∑ k log n ) O(\sum k \log n) O(∑klogn)。
#include <bits/stdc++.h>
#define init(x) memset (x,0,sizeof (x))
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define pii pair <int,int>
using namespace std;
const int MAX = 4e6 + 50;
const int MOD = 1e9 + 7;
inline int read ();
int t,n,q,cnt,ls[MAX],rs[MAX],tree[MAX];
class BIT
{
int n;vector <ll> c;
int lowbit (int x) {return x & (-x);}
public :
BIT (int n) : n (n),c (n + 1,0) {}
void modify (int x,int v) {for (int i = x;i <= n;i += lowbit (i)) c[i] += v;}
ll query (int x) {ll res = 0;for (int i = x;i;i -= lowbit (i)) res += c[i];return res;}
};
void modify (int &cur,int l,int r,int x,int v)
{
if (!cur) cur = ++cnt,ls[cur] = rs[cur] = tree[cur] = 0;
tree[cur] += v;
if (l == r) return ;
int mid = (l + r) >> 1;
if (x <= mid) modify (ls[cur],l,mid,x,v);
else modify (rs[cur],mid + 1,r,x,v);
}
int calc (vector <int> cur)
{
int res = 0;
for (auto v : cur) res += tree[v];
return res;
}
vector <int> next_L (vector <int> cur)
{
for (auto &v : cur) v = ls[v];
return cur;
}
vector <int> next_R (vector <int> cur)
{
for (auto &v : cur) v = rs[v];
return cur;
}
int search_L (vector <int> cur,int l,int r,int pos)
{
if (calc (cur) == r - l + 1) return 0;
if (l == r) return l;
int mid = (l + r) >> 1;
if (pos <= mid) return search_L (next_L (cur),l,mid,pos);
else
{
int res = search_L (next_R (cur),mid + 1,r,pos);
if (!res) return search_L (next_L (cur),l,mid,pos);
else return res;
}
}
int search_R (vector <int> cur,int l,int r,int pos)
{
if (calc (cur) == r - l + 1) return n + 1;
if (l == r) return l;
int mid = (l + r) >> 1;
if (pos > mid) return search_R (next_R (cur),mid + 1,r,pos);
else
{
int res = search_R (next_L (cur),l,mid,pos);
if (res == n + 1) return search_R (next_R (cur),mid + 1,r,pos);
else return res;
}
}
int main ()
{
t = read ();
while (t--)
{
n = read ();q = read ();cnt = 0;
vector <int> val (n + 1),col (n + 1),rt (n + 1,0);
BIT tr (n);
for (int i = 1;i <= n;++i) col[i] = read (),modify (rt[col[i]],1,n,i,1);
for (int i = 1;i <= n;++i) val[i] = read (),tr.modify (i,val[i]);
while (q--)
{
int ty = read ();
if (ty == 1)
{
int p = read (),x = read ();
modify (rt[col[p]],1,n,p,-1);
col[p] = x;
modify (rt[col[p]],1,n,p,1);
}
else if (ty == 2)
{
int p = read (),v = read ();
tr.modify (p,v - val[p]);
val[p] = v;
}
else
{
int st = read (),k = read ();
vector <int> p;
for (int i = 1;i <= k;++i)
{
int x = read ();
p.push_back (rt[x]);
}
int l = search_L (p,1,n,st),r = search_R (p,1,n,st);
printf ("%lld\n",tr.query (r - 1) - tr.query (l + 1 - 1));
}
}
}
return 0;
}
inline int read ()
{
int s = 0;int f = 1;
char ch = getchar ();
while ((ch < '0' || ch > '9') && ch != EOF)
{
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9')
{
s = s * 10 + ch - '0';
ch = getchar ();
}
return s * f;
}
2025.05.15 The 2024 ICPC Asia Hangzhou Regional Contest
上午考完期末,开启暑假生活!
省流: 6 6 6 题收尾。过题顺序 A,K,E,H,M,F。
可能是上午考线代考傻了,签到题写了半小时才过。 A A A 用并查集维护即可,可是一开始写得有点乱,WA 了 2 2 2 次才过。接着队友写 K,不知道怎么回事思路没问题就是过不了。我听完思路直接给他重写了,然后就过了,非常神奇(说明队友码力有点弱,需要加训~)。
接着 Zlw 佬开始敲 B,敲完交了以后才发现把题目理解成了或运算,于是乎,一直只能想到双 log 的做法。我这边看了下 E,一开始认为是 DP,想了一会儿发现更像是贪心。和 Zlw 佬进一步讨论了一下感觉没啥问题。设当前处在 f f f 层,找到 l l l 在 f f f 之下的 r r r 最大的那个,如果不存在,就需要花费额外的能量向上运动。等到达最顶端后在往下降,处理一下剩余的区间,此时不需要额外花费。因此直接可以优先队列维护,从而做到 O ( n log n ) O(n \log n) O(nlogn)。
Sky 这时候在写 M,写完以后发现题目看错,占了一会儿机时。趁着他在调的时候继续口胡下一题,是我最喜欢的构造!不难想到先取最长的链,设长度为 k k k,于是剩下 [ 1 , k − 1 ] [1,k - 1] [1,k−1] 的区间全部能够挂在这条链上。唯一需要考虑的就是有多条长度为 k k k 的链的情况,此时只要前面的区间没有都挂在根节点上就存在解。
M 还有一些问题,于是我把 E,H 这两题都实现了。接下去他俩一起在搞 M,我开始看 F。M 似乎进行数论分析和 ST 维护以后终于过了。F 是图论,容易想到 scc 缩点,难点是处理询问。不过询问又非常特殊,是在一条链上询问,因此就可以通过前缀和处理。但需要注意块内可能询问点并不完整,因此需要更多的处理。突然开窍,然后在比赛结束前 3 分钟通过了!
for (int i = 1;i <= n;++i) ++sz[scc[i]];
for (int i = 1;i <= k;++i)
for (int j = 1;j <= n;++j)
{
pre[i][j] = pre[i][j - 1];
if (scc[a[i][j]] != scc[a[i][j - 1]]) tot[i][j] = 1;
else pre[i][j] += tot[i][j - 1],tot[i][j] = tot[i][j - 1] + 1;
}
while (q--)
{
ll id = read (),l = read (),r = read ();
id = (id + ans) % k + 1;l = (l + ans) % n + 1,r = (r + ans) % n + 1;
if (scc[a[id][l]] == scc[a[id][r]]) ans = pre[id][r] - pre[id][l - 1] - (tot[id][l] - 1) * (r - l + 1);
else ans = pre[id][r] - pre[id][l - 1] - (sz[scc[a[id][l]]] - (tot[id][l] - 1)) * (tot[id][l] - 1);
printf ("%lld\n",ans);
}
总的来说,这场 6 题还是很不错的(似乎能银)。但是罚时过高,速度还是有点慢。看来,还是需要加训滴~
2025.05.16
我开始进一步学习计算几何,争取在省赛前能把这一块的模板弄全。具体内容就放在上面的博客里了。
2025.05.18
自己打了把西安交通大学2025年程序设计竞赛校赛(同步赛),被 F 题硬控了,最后八题收尾。
2025.05.19 The 2025 ICPC Wuhan Invitational Contest
A 签到,I 简单构造,I 无解判断写错 WA 了一发(阿巴阿巴)。
L 算是贪心,容易想到枚举端点位置,但是发现固定最大最小值后中位数位置不确定,于是改为枚举最小值和中位数。队友调了老半天才通过。
F 似乎题解是贪心,但是 Zlw 用背包配合 __int128 通过了,取模没取完整贡献一发罚时。
G 感觉有点典,容易想出把所有颜色分开考虑。这种棋盘就方案数有两种 DP,简单的就直接 O ( n m ) O(nm) O(nm) 遍历;复杂的依赖一种颜色的数量 O ( k ) O(k) O(k),进行 DP 容斥(CF559C)即可。于是想到分块做法,时间复杂度 O ( m n m n ) O(mn \sqrt {mn}) O(mnmn)。
M 超绝计算几何,一直调到最后。大致分为两类,到端点的距离以及与原点和垂足形成的直线到线段的交点的距离。设端点是
S
,
T
\text{S},\text{T}
S,T,首先做平面
OST
\text{OST}
OST,做垂足
F
F
F,若落在直线
OS
,
OT
\text{OS},\text{OT}
OS,OT 的那个区域之外,则只需要考虑前一种情况即可,否则两种情况都要考虑。其次需要考虑
∣
OF
∣
\mid\text{OF}\mid
∣OF∣ 已知时
O
F
\mathbf{OF}
OF 的方向性。最后,需要尤其注意一下精度和垂直的情况。我们写的时候 acos(x) 的参数由于精度问题落在了
[
−
1
,
1
]
[-1,1]
[−1,1] 之外,然后一直输出 nan,非常令人红温。不过在查看数据并 WA 无数次后终于通过了此题。
2025.05.21 The 2025 ICPC China Zhejiang Province Programming Contest
超多罚时场。
B,I 签到,然后我发现 D 是简单构造,三题一遍过,开局还算比较顺利。
接下去开了 L,由奶龙指认的奶龙一定不是奶龙为出发点,提出拓扑加贪心的算法。我开写,脑抽用 set 来维护最优作为奶龙的节点,可是似乎处理上有很大的细节漏洞,于是一直 WAWAWA,导致接下去的一个半小时没有过题。Zlw 和 Sky 在想 F,讨论出了拆点加 bfs 最短路的做法。被踹下去以后他们提交了三发后通过(WA 是 bfs 后忘记 push 新的节点了)。
这时候我在重构了若干次代码之后突然醒悟,只需要 O ( n ) O(n) O(n) 的拓扑排序即可实现。先处理链,遇到一个点标记为奶龙,指向的下一个点标记为非奶龙,然后再把下一个的下一个点入度减一。剩下为环的部分,如果未标记就记录个数 x x x,一段未标记中奶龙的个数就是 x 2 \frac{x}{2} 2x。再次重写,终于通过。【果然,写奶龙题人也会变唐,阿巴阿巴~~~】
Zlw 在之后尝试 A,作为一个数据结构大神,尝试用分块,莫队以及线段树的结合题切题。Sky 在看 G,我看 M。A 上机尝试并通过样例后提交,发现 TLE,调整分块参数后仍然无法通过。而 M 发现交互毫无意义,把题目转化为了已知与一顶点 P P P 到其它不相邻的顶点构成的线段相交的三角剖分数量,然后还原三角剖分。可惜没什么想法。
G 又想了贪心的想法,于是上机写。由于普通的贪心是 O ( T n k ) O(Tnk) O(Tnk) 的,我微微打表观察以后提出了一个先将每个数增加 max ( 0 , k − 100 n n ) \max (0,\frac{k - 100n}{n}) max(0,nk−100n) 后剩余部分再贪心的做法(其实严格来说, 100 100 100 应该替换为 max l i − min l i \max {l_i} - \min {l_i} maxli−minli,但是取极限差不多就是 100 100 100),此时经过估算应该能够通过。可是交上去后仍然 TLE,于是接下去的 n 发提交都是再尝试调参卡精度。Sky 弄了半天仍然不行,趁他上厕所的时候,我把他贪心改成优先队列,然后加了快读快写,把常数减小了 5 5 5 倍左右。终于,+10 以 956 ms 极限卡过此题(一共 113 个测试点可还行 qwq)。后来看了题解,发现是要二分操作的倍率,实在是深刻。
还是 6 题首尾,不知道什么时候可以突破捏~
2025.05.22 The 2024 ICPC Asia Shanghai Regional Contest
又难又屎的一场,赛时 5 题,赛后 7 题。
上来就被 I 签到给恶心了好几发,原因就是求的是最大值的模而非模意义下的最大值,因此取模要非常小心。 0 0 0 以及大于模数的情况都需要考虑到,非常容易出错。半小时才通过此题,而且 WA 了整整 7 次(显然是红温了)。
接下来 Sky 秒了博弈论 C,Zlw 开始写 B。但由于一些答案的合并问题,B 一直被硬控。接下来发现 D 是构造,果断将其丢给我。我手玩 D 发现只需要着重考虑最后四位的情况,于是疯狂分讨。上机写 D,发现样例水得一批,于是直接交,喜提 WA。下机思考,Zlw 终于过了 B,然后我发现有几种情况能够更优的构造,果断修改后通过。这时候 2 小时 4 题,除了罚时外到还行。
之后我又发现 H 是构造,于是又开始手玩。他俩在想 G,似乎是和二分中位数相关。H 玩了很久,由于是最优化步数的构造,我似乎没啥完整的想法,于是开始进击 M 计算几何。
M 似乎好做,很快地将问题分为了四类。设非上下表面的点的个数为 n n n(需要去重),然后将上下表面的点映射到二维平面中。于是有:
- n = 0 n = 0 n=0 恒有解。
- n = 1 n = 1 n=1 判断是否存在一条过定点的直线可以将剩余点归到直线的一侧。直接判断该点是否为凸包上的一点即可。
- n = 2 n = 2 n=2 判断过两个定点的圆能够将使得剩余点均在这个圆中。将点分为直线的两侧,然后根据圆周角的大小,一侧各剩下一点(没有的话肯定合法),判断四点共圆即可。特别地,如果点在直线上,则需要在线段上才符合。
- n = 3 n = 3 n=3 三点共线则不合法。否则取三点作圆,判断剩余点是否在圆上即可。
想完的时候 Zlw 刚好写完 G,于是我上机贺板子写 M。写完以后一直 WA,各种 corner 写挂,最后又被卡精度,直接写崩溃,直到结束也没过。赛后调了很久很久,然后又不断 hack 自己,最终才诞生了一份稍微好一点的屎。
auto f1 = [&] () -> bool
{
sp.push_back (P[0]);
auto hull = convex_hull (sp);
for (auto [x,y] : hull)
if (dcmp (x - P[0].x) == 0 && dcmp (y - P[0].y) == 0) return true;
return false;
};
auto f2 = [&] () -> bool
{
for (auto x : sp)
if (on_line (x,P[0],P[1]) && !on_seg (x,P[0],P[1])) return false;
LD d1 = 1000,d2 = 1000;
Point P1,P2;
for (auto x : sp)
{
if (on_line (x,P[0],P[1])) continue;
if (cross (P[1] - P[0],x - P[0]) > 0) {if (angle (x - P[1],x - P[0]) < d1) P1 = x,d1 = angle (x - P[1],x - P[0]);}
if (cross (P[1] - P[0],x - P[0]) < 0) {if (angle (x - P[1],x - P[0]) < d2) P2 = x,d2 = angle (x - P[1],x - P[0]);}
}
if (d1 == 1000 || d2 == 1000) return true;
Point F1 = foot (P1,P[0],P[1]),F2 = foot (P2,P[0],P[1]);
if (dcmp (dot (F1 - P[0],F1 - P[1])) > 0 && dcmp (dot (F2 - P[0],F2 - P[1])) > 0) return false;
Circle C1 = triangle_circum (P[0],P[1],P1),C2 = triangle_circum (P[0],P[1],P2);
return in_cir (C1,P2) && in_cir (C2,P1);
};
auto f3 = [&] () -> bool
{
if (dcmp (cross (P[0] - P[1],P[0] - P[2])) == 0) return false;
Circle C = triangle_circum (P[0],P[1],P[2]);
for (int i = 3;i < P.size ();++i)
if (dcmp (len (P[i] - C.O) - C.r) != 0) return false;
for (auto x : sp)
if (!in_cir (C,x)) return false;
return 1;
};
事实证明,还是要谨慎开计算几何。赛后发现我精准的选到了 H,M Medium hard \text{Medium hard} Medium hard,而跳过了中间的 F,J(非常离谱,看都没看)。看来策略还是需要在接下去进一步调整!
2025.05.23
补题,发现 H 最后构造出来剩余 . 的个数不会超过四个。于是就开始贪心构造,调整 6 种情况的优先级,试着试着突然发现对了。唯一的坑点就是要小心同色连成连通块,直接暴力判断后调整。放一下屎山代码:
int main ()
{
n = read ();int ans = 0;
vector <vector <char>> a (n + 5,vector <char> (n + 5,'.'));
vector <vector <char>> b (n + 5,vector <char> (n + 5,'.'));
auto check = [&] (int x,int y) -> bool {return !(x < y || x <= 0 || y <= 0 || x > n || a[x][y] != '.');};
auto same = [&] (char ch,int x,int y) -> bool {return ch == a[x][y - 1] || ch == a[x][y + 1] || ch == a[x - 1][y - 1] || ch == a[x - 1][y] || ch == a[x + 1][y] || ch == a[x + 1][y + 1];};
for (int i = n;i;--i)
{
for (int j = 1;j <= i;++j)
{
if (i == n && j == 1) continue;
if (check (i,j) && check (i,j + 1) && check (i - 1,j - 1))
{
while (same (char (op + 'A'),i,j) || same (char (op + 'A'),i,j + 1) || same (char (op + 'A'),i - 1,j - 1)) ++op,op %= 26;
a[i][j] = a[i][j + 1] = a[i - 1][j - 1] = char (op + 'A');
++ans;continue;
}
if (check (i,j) && check (i,j + 1) && check (i - 1,j + 1))
{
while (same (char (op + 'A'),i,j) || same (char (op + 'A'),i,j + 1) || same (char (op + 'A'),i - 1,j + 1)) ++op,op %= 26;
a[i][j] = a[i][j + 1] = a[i - 1][j + 1] = char (op + 'A');
++ans;continue;
}
if (check (i - 1,j - 2) && check (i - 1,j - 1) && check (i,j))
{
while (same (char (op + 'A'),i - 1,j - 2) || same (char (op + 'A'),i - 1,j + 1) || same (char (op + 'A'),i,j)) ++op,op %= 26;
a[i - 1][j - 2] = a[i - 1][j - 1] = a[i][j] = char (op + 'A');
++ans;continue;
}
if (check (i,j) && check (i - 1,j - 1) && check (i - 2,j - 1))
{
while (same (char (op + 'A'),i,j) || same (char (op + 'A'),i - 1,j - 1) || same (char (op + 'A'),i - 2,j - 1)) ++op,op %= 26;
a[i][j] = a[i - 1][j - 1] = a[i - 2][j - 1] = char (op + 'A');
++ans;continue;
}
if (check (i,j) && check (i - 1,j) && check (i - 1,j + 1))
{
while (same (char (op + 'A'),i,j) || same (char (op + 'A'),i - 1,j) || same (char (op + 'A'),i - 1,j + 1)) ++op,op %= 26;
a[i - 1][j] = a[i - 1][j + 1] = a[i][j] = char (op + 'A');
++ans;continue;
}
if (check (i - 1,j) && check (i,j) && check (i - 2,j - 1))
{
while (same (char (op + 'A'),i,j) || same (char (op + 'A'),i - 1,j) || same (char (op + 'A'),i - 2,j - 1)) ++op,op %= 26;
a[i - 1][j] = a[i][j] = a[i - 2][j - 1] = char (op + 'A');
++ans;continue;
}
}
}
for (int i = 1;i <= n;++i)
{
for (int j = 1;j <= n - i;++j) putchar (' ');
for (int j = 1;j <= i;++j)
{
putchar (a[i][j]);
putchar (j == i ? '\n' : ' ');
}
}
return 0;
}
2025.05.24
仍然是调整日。昨天看其它队伍 vp 的时候发现自己的数论实在是太差了,遂补一下 exgcd。
求满足 ∀ i ∈ [ 1 , n ] , n ( n + 1 ) 2 ≡ 0 ( m o d p i ) \forall i \in [1,n],\frac{n(n + 1)}{2} \equiv 0\pmod {p_i} ∀i∈[1,n],2n(n+1)≡0(modpi) 的最小正整数 n n n。
设 l = 2 × lcm ( p 1 , p 2 , ⋯ , p n ) l = 2\times \operatorname{lcm} (p_1,p_2,\cdots,p_n) l=2×lcm(p1,p2,⋯,pn)。转换为最小化 n n n,使得 n ( n + 1 ) ≡ 0 ( m o d l ) n(n + 1) \equiv 0 \pmod l n(n+1)≡0(modl) 成立。
由于 gcd ( n , n + 1 ) = 1 \gcd (n,n + 1) = 1 gcd(n,n+1)=1,因此 l l l 的一种因子只会分给 n n n 或 n + 1 n + 1 n+1 其中一个。由于 l l l 的因子数量最多为 15 15 15 个,因此状压枚举即可。
对于当前状态 s t st st,令 x = ∏ i ∈ s t p i , y = ∏ j ∈ s t ∁ p j x = \mathop{\prod}_{\substack{i \in st}} p_i,y = \mathop{\prod}_{\substack{j \in st^\complement}} p_j x=∏i∈stpi,y=∏j∈st∁pj,则 n = a x , n + 1 = b y n = ax,n + 1 = by n=ax,n+1=by,作差可知 − a x + b y = 1 -ax + by = 1 −ax+by=1。由于 gcd ( a , b ) = 1 \gcd (a,b) = 1 gcd(a,b)=1,方程有解,直接跑 exgcd,然后求 min { a x } \min \{ax\} min{ax} 即可。
终于把上个赛季重庆站的题目给补了。(以下证明部分参考 CCPC2024 重庆_补题记录ADFGH)
命题
若 b = w 2 x 5 y b = w2^x5^y b=w2x5y,则最优条件下 d d d 一定可以表示为 w 2 x ′ 5 y ′ w2^{x\prime}5^{y\prime} w2x′5y′(其中 w , z w,z w,z 不再含有 2 , 5 2,5 2,5 的幂次)。
证明
设 d = z 2 x ′ 5 y ′ d = z2^{x\prime}5^{y\prime} d=z2x′5y′,则 a b + c d = a z 2 x ′ 5 y ′ + w c 2 x 5 y w z 2 x + x ′ 5 y + y ′ \frac{a}{b} + \frac{c}{d} = \frac{az2^{x\prime}5^{y\prime} + wc2^x5^y}{wz2^{x + x\prime}5^{y + y\prime}} ba+dc=wz2x+x′5y+y′az2x′5y′+wc2x5y。接下来处理分子,由于最后是有限小数,一定存在 k k k 使得 a z 2 x ′ 5 y ′ + w c 2 x 5 y = k w z az2^{x\prime}5^{y\prime} + wc2^x5^y = kwz az2x′5y′+wc2x5y=kwz 成立。
把 c , k c,k c,k 看作未知数,写成 exgcd 的标准形式:
( − w 2 x 5 y ) × c + w z × k = a z 2 x ′ 5 y ′ (-w2^x5^y) \times c + wz \times k = az2^{x\prime}5^{y\prime} (−w2x5y)×c+wz×k=az2x′5y′
有解当且仅当 gcd ( − w 2 x 5 y , w z ) = w ∣ a z 2 x ′ 5 y ′ \gcd(-w2^x5^y,wz) = w \mid az2^{x\prime}5^{y\prime} gcd(−w2x5y,wz)=w∣az2x′5y′,也就是 w ∣ a z w \mid az w∣az。由于 gcd ( a , b ) = 1 \gcd (a,b) = 1 gcd(a,b)=1,则 gcd ( a , w ) = 1 \gcd (a,w) = 1 gcd(a,w)=1,因此得到 w ∣ z w \mid z w∣z。
同理,把 a , k a,k a,k 当作未知数,可以得到 z ∣ w z \mid w z∣w。
综上, z = w z = w z=w 成立。
因此, a b + c d = a 2 x ′ 5 y ′ + c 2 x 5 y w 2 x + x ′ 5 y + y ′ \frac{a}{b} + \frac{c}{d} = \frac{a2^{x\prime}5^{y\prime} + c2^x5^y}{w2^{x + x\prime}5^{y + y\prime}} ba+dc=w2x+x′5y+y′a2x′5y′+c2x5y。由于最后是有限小数,所以可以进一步把和表示为 k w w 2 x + x ′ 5 y + y ′ = k w 2 b d \frac{kw}{w2^{x + x\prime}5^{y + y\prime}} = \frac{kw^2}{bd} w2x+x′5y+y′kw=bdkw2。枚举 d d d 中的 x ′ , y ′ x^{\prime},y^{\prime} x′,y′,然后求不定方程
b × c − w 2 × k = − a d b \times c - w^2 \times k = -ad b×c−w2×k=−ad
直接 exgcd 后求出 c c c 的最小值即可。
2025.05.25 第十届中国大学生程序设计竞赛 济南站(CCPC 2024 Jinan Site)
题目好难,就做出 4 题,倒闭!
A,J 签到,但是 A 被我 WA 了一发。之后想 F,Zlw 用了数论做法,还用到了莫比乌斯反演,似乎复杂化了,WA 了好几次以后才过(应该已经是 2.5 h 左右了)。
我看了 E,感觉是个超级分类讨论题,于是开始疯狂推公式。Sky 看 B,是个模拟+暴力题,但是不好写。E 我分了 7 类,感觉差不多了就上机写。由于涉及高精度,于是果断使用 Python。样例真的水的一批,过了样例交然后喜提 WA。
静态调试无果,于是下机看 I 换换脑子,Sky 上机写 B。I 构造容易想到自底往上,同一个子树内的点可以直接合并,然后想到链的做法不太好搞。这时候 Sky 过了 B,于是我就没再细想,把题丢给他俩,然后调 E 去了。
事实证明,这是这场比赛的败笔。接下来的时间内,E 一直被形如 ABAB...A 需要对最后一个 A 调整的 case 所困扰,而他俩直接把 I 想复杂,在做树上 DP。于是一直红温到比赛结束。
后来才发现,E 的 ABAB...A 的调整还需要细化。假设直接按照这个方案会浪费掉
x
x
x 的距离,则有:
-
B最多可以移掉 min ( x , ⌊ D X + Y ⌋ × Y ) \min (x,\lfloor\frac{D}{X + Y}\rfloor \times Y) min(x,⌊X+YD⌋×Y)。 -
变为
AA...ABAB的形式B最多有 min ( D − ⌊ D X ⌋ × X , ⌊ D X ⌋ × Y ) \min (D - \lfloor\frac{D}{X}\rfloor \times X,\lfloor\frac{D}{X}\rfloor \times Y) min(D−⌊XD⌋×X,⌊XD⌋×Y)。
最终代码:
def up (x,y) : return (x - 1) // y + 1
def solve (A,B,C,X,Y,D) :
if D <= X : return A
if D <= X + Y : return min (A + B * (D - X),A * up (D,X),A * (D // X) + B * (D % X))
ans = A * up (D,X) #AA...A
if D % X <= Y : ans = min (ans,(D // X) * A + B * (D % X)) #AA...B
else : ans = min (ans,(D // X) * A + B * Y + (D % X - Y) * C) #AA...BC
ans = min (ans,A + B * Y + (D - X - Y) * C) #ABC
if D % (X + Y) > X : ans = min (ans,(D // (X + Y)) * (A + B * Y) + A + B * (D % (X + Y) - X)) #ABAB...AB
ans = min (ans,D // X * A + min (D - D // X * X,D // X * Y) * B + (D - D // X * X - min (D - D // X * X,D // X * Y)) * C) # AA..ABAB..
ans = min (ans,(D // (X + Y)) * (A + B * Y) + A - B * min (D // (X + Y) * Y,X - D % (X + Y))) #ABAB...A
ans = min (ans,(D // (X + Y)) * (A + B * Y) + C * (D - (X + Y) * (D // (X + Y)))) #ABAB...C
return ans
而 I,那种链的情况也很好做,直接记录下剩余的点然后往上传即可。注意如果一个子树内,优先合并单点,再合并向上传过的点(因为单点不能形成自环)。赛后 Sky 写了 I,一发通过;我也在发现 corner case 以后 WA 了几发后通过。简直破大防!
C 纯构造竟然没发现,感觉非常好做。POP n GOTO n + 1; PUSH n GOTO n 就能形成链,POP n GOTO n + 1; PUSH n GOTO 1 就能翻倍,于是这道题做完了。
void dfs (ll x)
{
if (!x) return ;
if (x / 2 % 2 == 1)
{
dfs (x / 2 - 1);++cnt;
printf ("POP %d GOTO %d; PUSH %d GOTO %d\n",cnt,cnt + 1,cnt,1);
}
else
{
dfs (x - 2);++cnt;
printf ("POP %d GOTO %d; PUSH %d GOTO %d\n",cnt,cnt + 1,cnt,cnt);
}
}
2025.05.26 The 2024 ICPC Southeastern Europe Regional Contest (SEERC 2024)
做点欧洲的区域赛来换换脑子。
开局 Zlw 发现 A 是 n 2 n^2 n2 的做法,于是不需要换根 DP 直接暴力。我在看 D,感觉变种的 Nim 游戏并不是那么好做,但 Sky 发现后手是需要连续操作 n n n 轮,与堆数相同,那么这道题瞬间变唐。于是立刻开写,但被全是 0 0 0 的 corner case 淦了一发罚时。
在 A 通过之后,我发现 G 是一个简单 DP,直接开写,一发通过。之后 Sky 让我看看 J,如果是极值的情况答案很简单,然后发现如果是被最大最小值加在中间时,只需要多一次操作就能将其归约到前一种情况,于是火速过 J。Zlw 在想 L,猜了一个想法并手搓平衡树,竟然一发通过,不知道有没有想复杂。
大家一起看 H,猜测是贪心但是又有点不会证明。这时候 Zlw 想到了一个网络流做法并保证了正确性,由于我和 Sky 对这题都没啥想法,于是就让 Zlw 开写(因此也在与正解越走越晚)。好不容易写完以后,一交 TLE,这下完蛋,被 m m m 很小的点卡了,也没法优化。好,这下被真的卡住了,已经将近 1.5 h 没有过题。
好在 Zlw 重新思考贪心做法,并用尝试优先队列去维护,在四小时不到一点的时候通过。我和 Sky 在开 K,我提出维护最初每一个字符所扩展到的区间 l i , r i l_i,r_i li,ri,Sky 推了推发现是可维护的(虽然要分好几类)。但 Sky 并不是很擅长线段树,于是我先开始上机写区间加和乘,然后让他报给我区间更新的具体内容。本来是报着打完这道题还要调试一万年的,但是我稍微修改了一下我查询写挂的地方,之后竟然直接过样例。直接交!RE!噢是有个地方没开 long long!再交!AC!我们狂喜!
还剩下 20 min,尝试开 C 交互,但是没啥想法,最后 7 题收尾!
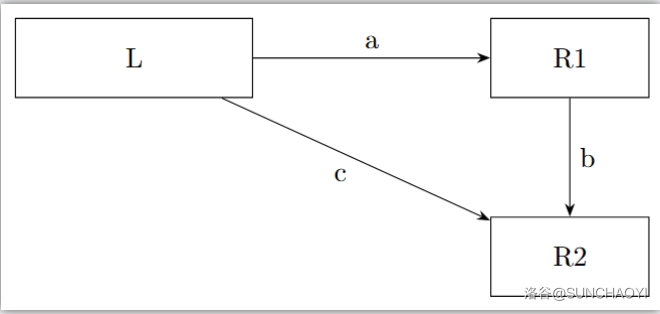
C 从集合与集合之间的询问出发,通过二分找到能与集合连边的单点。具体来说, L L L 与 R = R 1 ∪ R 2 R = R_1 \cup R_2 R=R1∪R2 获得 a + c a + c a+c,然后二分右侧获得 R 1 , R 2 R_1,R_2 R1,R2。之后进行进一步地询问, L ∪ R 1 L\cup R_1 L∪R1 与 R 2 R_2 R2 询问获得 b + c b + c b+c,, L ∪ R 2 L \cup R_2 L∪R2 与 R 1 R_1 R1 询问获得 a + b a + b a+b。若 a + b + a + c = b + c a + b + a + c = b + c a+b+a+c=b+c,则 a = 0 a = 0 a=0,也就说明 R R R 中只有 R 2 R_2 R2 与 L L L 有直接连边。因此 n n n 轮每次获得一个直接相连的点,询问次数在 n + 2 n log n n + 2n \log n n+2nlogn。
2025.05.27 The 2024 ICPC Central Europe Regional Contest
开局 B,C,D 签到。然后看 L,搜索题的变种,一眼猜测需要再加一个维度表示朝向,但是不太想写,丢给 Zlw 了。
看 I,没想法;看 K,以为是构造,但是发现可能是搜索。发现奇数和偶数的位置一定有一种是需要全填的,但是剩余的位置还有 32 个,直接暴力不可过,于是开始各种乱搞。但是怎么尝试都 WA,于是开摆(
Sky 成功把 I 做出来了,真是太有实粒了!先入为主的会去想行与行之间的关系,可是如果考虑列,对于第
i
i
i 个位置,进行变换
k
→
k
+
1
k \to k+1
k→k+1,即
S
k
[
i
]
=
S
k
+
1
[
P
(
i
)
]
S_k[i] = S_{k+1}[P(i)]
Sk[i]=Sk+1[P(i)],将这条约束在
k
=
1
,
2
,
…
,
k
−
1
k=1,2,\ldots,k-1
k=1,2,…,k−1 都写出来:
(
S
1
[
i
]
S
2
[
i
]
⋮
S
k
−
1
[
i
]
)
→
(
S
2
[
P
(
i
)
]
S
3
[
P
(
i
)
]
⋮
S
k
[
P
(
i
)
]
)
\begin{pmatrix} S_1[i] \\ S_2[i] \\ \vdots \\ S_{k-1}[i] \end{pmatrix} \to \begin{pmatrix} S_2[P(i)] \\ S_3[P(i)] \\ \vdots \\ S_k[P(i)] \end{pmatrix}
S1[i]S2[i]⋮Sk−1[i]
→
S2[P(i)]S3[P(i)]⋮Sk[P(i)]
也就是说,用第 1 , ⋯ , k − 1 1,\cdots,k−1 1,⋯,k−1 轮的列向量去匹配第 2 , ⋯ , k 2,\cdots,k 2,⋯,k 轮的列向量,贪心找最小值即可。
Zlw 继续开 F 数据结构,上机写着写着感觉太麻烦了,又开摆(
最后 5 题收尾了(太累了,开启休整模式 qwq)。赛后还是看了下 K 别人的代码,发现就是疯狂减枝的爆搜,这种题都能上区域赛?有点离谱了!
2025.05.29 The 2023 ICPC Asia Jinan Regional Contest
D 签到,鹊巢原理之后就会异常好做(Zlw 佬一开始没看出来,差点写成数位 DP)。Sky 猜了一个 I 的结论,一发通过!我看 A,一下子没想法,和 Zlw 讨论了一下突然会了,只要贪心还原,然后只要有一个右括号的右侧存在一个左括号,并且中间是合法的即可。感觉很对,丢给 Zlw 去写了。
尝试看 K,猜想二分,但是 check 很难写。Zlw 佬看了题,一眼中位数最优,然后尝试用对顶堆去维护,似乎多了一个
log
\log
log,但是好在一发通过!接着 Sky 喂给我一个 G 题的做法,直接上机写并查集,写完后 WA,我思考了一会儿想到 1010 1100 这种既互斥又互补的做法,本来想要特判,但是发现这是一类没有考虑到的情况。Zlw 即时的提出了这就是 2-SAT,直接上扩展域并查集即可。修了好久,总算通过了。其间红温了好久,下机缓了缓,而趁着这个时间他俩讨论出了 E 的网络流做法,并一发 AC,真的太有实粒了!
最后开了 M,想到先求凸包,然后枚举一个基准点,用极角排序和双指针来维护答案,时间复杂度
O
(
n
2
log
n
)
O(n^2 \log n)
O(n2logn)。想得非常正确,但由于对极角排序非常的不熟悉,用 atan2 超时了,然后想要改成叉乘却又发现不对,还剩一个小时但是也没调出来,成罪人了(
好在六题收尾,并且只有一发罚时!
赛后补题,发现 M 的致命错误:
-
制作模板的时候写的是 0-vector,而一开始自己写的却是 1-vector。
-
直接预处理了
atan2后再排序,把超时问题解决了,这个函数是真的慢啊!!! -
判断点是否在三角形内用的是角度的做法,但是有精度误差导致一直 WA 掉。最后改成看穿入穿出的奇偶性之后就对了。
int in_Poly (vector <Point> P,Point A)
{
int cnt = 0,n = P.size ();
for (int i = 0;i < n;++i)
{
int j = (i + 1) % n;
if (on_seg (A,P[i],P[j])) return 2;// on the edge
if (A.y >= min (P[i].y,P[j].y) && A.y < max (P[i].y,P[j].y)) // the intersection is on the right
cnt += dcmp (((A.y - P[i].y) * (P[j].x - P[i].x) / (P[j].y - P[i].y) + P[i].x) - A.x) > 0;
}
return cnt & 1;
}
2025.05.30 第九届中国大学生程序设计竞赛 桂林站(CCPC 2023 Guilin Site)
省赛前最后一训!
G 题面写得实在有点一言难尽,读懂题目后发现是弱智题,速速通过。接着又很快的签完 M。
之后看了 K,发现 n × m ≤ 180 n \times m \le 180 n×m≤180 的数据范围很诡异,发现可以针对 n n n 较小和 m m m 较小写暴力,调了一会儿三发通过(之后看题解发现答案数量有限,直接用 map 跑暴力即可)。
之后看 B,C,发现都不好做,于是开始坐牢。B 的贪心情况很多,Sky 一直在红温,我和 Zlw 尝试做 C。C 的式子很是特殊,由于异或是不进位加法,所以 lcm { a i j } ∣ ⨁ j = 1 m a i j \operatorname{lcm} \{a_{i_j}\} \mid \bigoplus_{j=1}^m a_{i_j} lcm{aij}∣⨁j=1maij 成立只有 ⨁ j = 1 m a i j = 0 \bigoplus_{j=1}^m a_{i_j} = 0 ⨁j=1maij=0 或 ⨁ j = 1 m a i j = lcm { a i j } = max { a i j } \bigoplus_{j=1}^m a_{i_j} = \operatorname{lcm} \{a_{i_j}\} = \max \{a_{i_j}\} ⨁j=1maij=lcm{aij}=max{aij}。对于第一种情况,直接跑线性基,答案为 2 n − r 2^{n - r} 2n−r, r r r 为秩。对于第二种情况,先用 log \log log 复杂度预处理每一个最大值的约数,然后两边同时异或上最大值就规约为第一种情况,再跑线性基即可,放个代码:
int main ()
{
vector <vector <int>> d (200001);
for (int i = 1;i <= 200000;++i)
for (int j = i;j <= 200000;j += i) d[j].push_back (i);
t = read ();
while (t--)
{
n = read ();
vector <int> cnt (n + 1,0);Basis <int> basis (n,20);
for (int i = 0;i < n;++i)
{
int x = read ();++cnt[x];
basis.modify (x);
}
int ans = (qpow (2,n - basis.query ()) + MOD - 1) % MOD;
for (int i = 1;i <= n;++i)
{
if (!cnt[i]) continue;
int tot = 0;
Basis <int> tmp (n,20);
for (auto v : d[i])
if (cnt[v]) tmp.modify (v),tot += cnt[v];
ans = (ans + qpow (2,tot - tmp.query ()) % MOD) % MOD;
}
printf ("%d\n",ans);
}
return 0;
}
之后 Sky 尝试写 B,但是一直在调。我和 Zlw 讨论了 H 并得到了一个感觉相当正确的猜想。Zlw 还看了 I,不过没有什么非常好的想法。
打到后面稍稍有点累,于是 B 没调出来。H 我就最后 10 min 上机尝试写了一下,结果被 corner case 卡了。
屎到底还是要吃的。赛后 Zlw 看了 I 的题解恍然大悟,光速过题;Sky 在发现自己的程序被卡超时后好不容易改成 log \log log 并通过了 B;而我,在发现还要记录叶子节点上 1 1 1 的个数(可以合成一个 2 2 2)后也通过了 H。
auto dfs = [&] (auto self,int u,int fa) -> void
{
w[u] = a[u];one[u] = a[u] == 1;
for (auto v : ve[u])
{
if (v == fa) continue;
self (self,v,u);
w[u] += w[v];
odd[u] = min (odd[u],odd[v]);
even[u] = min (even[u],even[v]);
one[u] += one[v];
}
if (w[u] & 1) odd[u] = min (odd[u],w[u]);
else if (w[u] != 0) even[u] = min (even[u],w[u]);
if (w[u] < k) return ;
if (w[u] == k) ++ans,w[u] = one[u] = 0,odd[u] = even[u] = INF;
else if (w[u] > k)
{
int del = w[u] - k;
if (del % 2 == 1 && odd[u] <= del) ++ans,w[u] = 0,odd[u] = even[u] = INF;
if (del % 2 == 0 && (even[u] <= del || one[u] >= 2)) ++ans,w[u] = one[u] = 0,odd[u] = even[u] = INF;
}
};
害,只不过赛时啥实力不剩,只剩下红温了……
2025.06.02 省赛 The 2025 Guangdong Provincial Collegiate Programming Contest
出征省赛!深圳技术大学的校园真是开放,进出门完全没有人管,校园很大,而且厕所里有空调!

进到机房以后,发现有 vscode,然后监考一会儿说可以用,一会儿又说不可以(笑话)。在延迟了 15 min 左右以后终于开始比赛,好在 PTA 这次没炸。
发现 D 是签到,Zlw 先敲了,然后发现 dev 的 -std=c++14 不能用,改成 c++11,仍然报错!好了,这下直接退化成 c++98,作为一个 auto 选手,直接倒闭(于是接下来,我都拒绝上机。
D 写完后,Sky 开始写模拟 F,写了几发都没过,于是 Zlw 先上机一发过了 G。然后我再听了 Sky 的思路以后,极不情愿的上机开始调,看了半天以后直接重构,一交继续 WA,想了一会儿以后发现思路有问题,加了一个贪心的排序以后再交,还是 WA!我开始红温,再看了很多遍以后发现有个地方忘记写 + 了,赶紧改,终于再 WA6 以后通过,成大罪人了。
之后是 H,发现贪心连边以后直接跑 DP 就能求出所有本质不同的子串,两发通过。然后看了 J,和 Zlw 简单对了思路以后发现用优先队列维护即可。由于我不想再上机写代码,于是继续 push 了 Zlw。
还有将近两小时,看 I,我先想了大概的思路,但是要上机敲代码的时候发现漏考虑了容斥的部分情况。于是 Zlw 继续发力,提出直接暴力考虑三列的情况。写了半天在还有不到半小时以后过了样例,直接交!WA!
坏了,继续调试,发现写得似乎都没问题,继续交了几发,一直到赛后也没过……五题收尾!
本来以为只有 Cu,后来发现 Ag 的比例也有 20 % 20\% 20%,最后 rk62 Ag(还被另一支校队伍从 4 → 6 4 \to 6 4→6 翻盘,真的是不封榜不会写代码了)。
赛后补题:
-
I 发现看错题了,有一只队伍需要强制选择,而我们在一次次转述题意之后出现了差错,导致没过题的惨剧。也就是说,我们的方法做成了更加复杂的版本,因此我加了点补丁以后直接过了。
-
A Zlw 的思路大致正确,于是赛后交了几发以后通过。其间 WA 时因为某些 long long 和 __int128 的问题,最后跪着接(
#define long long __int128) 就过了。 -
我补了 K,直接上哈希。发现答案递增,然后用哈希判断回文,用哈希和等比数列公式验证是否存在循环节。直接枚举答案以及 [ 1 , i ] [1,i] [1,i] 的询问即可。
Hash dl (s);reverse (s.begin (),s.end ());Hash dr (s);
for (int i = 1;i <= n;++i)
{
auto check = [&] (int x) -> bool
{
if (x == 1) return dl.get (1,i) == ((dl.get (1,1) * (Z <ll,MOD> (1) - dl.get_pw (i))) / (Z <ll,MOD> (1) - base));
if (x * 2 - 1 >= i)
{
Z <ll,MOD> dx = dl.get (2 * x - i,x),dy = dr.get (n - i + 1,n - x + 1);
return dx == dy;
}
int r = x * 2 - 1;
Z <ll,MOD> dx = dl.get (1,r),dy = dr.get (n - r + 1,n);
if (dx != dy) return false;
--r;
dx = dl.get (1,r) * (Z <ll,MOD> (1) - (dl.get_pw (r) ^ (i / r))) / (Z <ll,MOD> (1) - dl.get_pw (r));
dx = dx * dl.get_pw (i % r) + dl.get (1,i % r);
return dx == dl.get (1,i);
};
for (int j = res;j <= i;++j)
if (check (j)) {res = j;break;}
ans ^= 1ll * i * res;
}
8-9 月训练
2025牛客暑期多校训练记录
2025.08.30 CCPC 2023 Harbin Site
D,G 被 Zlw 秒了,J,M 被 Sky 秒了,B,L 被 Zlw 救了!
B 看上去是签到,我先上机开写。注意到了多次除以 2 2 2 有可能会造成精度问题,所以就加了个 eps。但是交上去还是 WA 了,这时候被 Zlw 救救,说可以把除以 2 2 2 移项改为乘 2 2 2,然后用 Python 来写。我果断采取建议,修改后通过!
接下去 M 是一道简单模拟,就交给 Sky 来写。花了 20 min 左右,过样例以后一发通过。
我接下去看了 L,想到可以固定第一位数,然后后面的数通过 2 操作在转,类似插入排序的原理。但是在实现上出现了问题,没有考虑到第一个位置数的顺序问题从而无法正确排序。
Zlw 上来就在看 D,一道数论和图论的结合题。佬在想明白只需要考虑价值为 ω ( w ) \omega(w) ω(w) 和 ω ( w + 1 ) \omega(w + 1) ω(w+1) 的边以后就会了,预处理后直接最小生成树即可。后来看了 XCPC board,发现差一发就是一血,是一道 Au 题!
写完 D 后 Zlw 佬看我红温了,于是交流了一下指出我的问题,并把我踹下去重新实现了。
我和 Sky 开始讨论 J 博弈论。Sky 首先列出了很大的一张表格,尝试去找规律。然后我对于一棵树,根据奇偶性,提出了点奇数删边,偶数边删点的猜想。但是在由树变为森林的时候,两条链(3 + 2)构成的情况的答案数量产生了疑问,似乎在一定程度上需要把猜想反过来。
继续手动模拟 SG 函数,突然发现偶数边偶数点的情况下答案都是 0 0 0,又试了几个确定了这个猜想。于是题目变成分类讨论度数即可。
我们卡 G 也有点时间,然后我突然点出墙体只有竖着的,于是简化了问题。主要是连续两行之间的合并,利用双指针就能实现,然后最后只需要根据边数和点数判断是否为一棵树即可。注意,$n \ge 2 $ 时
m
>
2
×
1
0
5
m > 2 \times 10^5
m>2×105 显然为 No,但是
n
=
1
n = 1
n=1 时需要特判。于是我们在这里挂了一发。
总体来说这场打得不错,对照着 XCPC board 似乎差三名就能 Au,怪我 L 写得慢还写红温了……
2025.08.31 CCPC 2023 Qinhuangdao Site
A 是简单构造,花费 2 s 想到解法,全部可以构造成互质的情况,但是第一发 WA。先让 Sky 来写 G,答案就是 ∑ i = 2 n ∣ a i − a i − 1 ∣ + ∣ b i − b i − 1 ∣ \sum \limits_{i = 2} ^ n |a_i - a_{i - 1}| + |b_i - b_{i - 1}| i=2∑n∣ai−ai−1∣+∣bi−bi−1∣。
然后发现 A 题目保证 k ≥ 2 n k \ge 2n k≥2n 但是我只用了 2 n − 1 2n - 1 2n−1 个,发现没有保证第一个数和最后一个数的行列都至少有两个数字,修补一下就过了。
Zlw 看了 J,是一道简单子集枚举的状压,时间复杂度为 O ( 3 n + n 2 n ) O(3^n + n2^n) O(3n+n2n)。
接下来两小时内无人过题……
D 被 Zlw 想到了一个 DP,然后用双指针和平衡树在维护,感觉很是复杂。提交了好几遍都没过,对拍还没拍出来。然后 Sky 还开了 F,要求相邻两数得是质数,然后注意到 1 + 1 = 2 1 + 1 = 2 1+1=2 这个质数比较特殊,接下去没什么进展。
然后我突然灵光一现,想到了 D 可能是个贪心。由于优惠券可以叠加使用,可以先将优惠券按照过期时间排序,然后对于当前优惠券,选择 [ 1 , r i ] [1,r_i] [1,ri] 范围内 a i a_i ai 最小的那个,然后 a i ← a i − w i a_i \leftarrow a_i - w_i ai←ai−wi,最后直接对 a i a_i ai 排序即可。于是上机写,让 Zlw 去看 Sky 的题。
我在写的时候,Zlw 提出一个 DP 的写法, d p i , 0 / 1 / 2 / 3 dp_{i,0/1/2/3} dpi,0/1/2/3 表示填第 i i i 个数时, i i i 改为偶数,不为 1 1 1 的奇数,为 1 1 1,不变这四种情况,然后就能够转移。
D 对于更新 a i a_i ai 没啥好的想法,直接上线段树进行更新,写完以后一遍过样例,直接交,终于 AC!
Zlw 的 F 也过样例了,但是 WA。叫我过去瞅瞅,一行行给我翻译,然后我突然发现有一种情况转移的时候漏掉了固定为 1 1 1 的情况,修改以后直接通过。
接下去看了 M,但是没啥想法,于是下班。事实证明,全队的树形 dp 不太行(牛客的时候遇到树形 dp 的中档题也没解出来)。最后 5 5 5 题,但是我们的 DF 都是三小时的时候才过,于是在 XCPC board 上只能排到 Cu!
2025.09.05 The 15th Shandong CCPC Provincial Collegiate Programming Contest
临时加训了一场简单的 SUA 省赛场,用来增强信心!Zlw 佬还在赛时秒了 E,一开始 TLE,稍微优化了一下就过了,结果还是一血来着!
网络预选赛
2025.09.07 The 2025 ICPC Asia East Continent Online Contest (I)
赛时 6 题,最后两小时有点倒闭,没有过题,在同校中排 rk3(由于前期光速过题,我们是六题队在排在前面的。但是非常可恶,被牢周队在封榜以后反超了)。
G 签到,其实是 Sky 做出来的,一开始 Zlw 以为连通就可以,但是突然发现小的数会卡在前面阻止别人交换。Sky突然说必须要连 1 → 2 → ⋯ → n 1\rightarrow 2\rightarrow\cdots\rightarrow n 1→2→⋯→n,Zlw 觉得有道理,但是由于数组开小了段错误了一发。
接着 A 大模拟,趁着队友上机仔细想了细节,后来上机一发过,这是好的!
刚下机队友就发现 B 是个大诈骗,发现 gcd \gcd gcd 的可能结果是 n n n 的约数,理论上可以枚举,然后计算每个 gcd \gcd gcd 的方案数。一开始看错题了以为 a a a 是给定的,后面发现 a i = i a_i=i ai=i,突然想到对于每一个约数的同余结果是相同的,在想容斥的过程中突然发现只要连续的删除数对于结果的影响理应是相同的。所以直接删 [ 1 , K ] [1,K] [1,K] 理论可行。验证了一下确实与样例结果相同,提交了一下过了。直接输出 1 ∼ k 1 \sim k 1∼k 就过了!
接下去队友发现不太会 D,于是我开始尝试看。他俩开始讨论 M,很明显的分层图最短路,只不过 O ( n m ( log n + log m ) ) O(nm(\log n+\log m)) O(nm(logn+logm)) 的复杂度很劝退。进一步发现可以一层层转移,每一层只需要考虑树上的松弛操作,很容易跑不满,加上单层转移的时候可以做到 O ( n m log n ) O(nm\log n) O(nmlogn) ,比上面的复杂度稍有优化,且常数小不少,写了一下 0.9 s 0.9s 0.9s 跑过。写完以后 pta 在队长机上崩了一会儿,自带罚时,捣鼓两分钟以后才交了上去,好在一发通过。
D 我觉得可能是贪心,考虑链的情况,如果出现峰值,就把差值绝对值小的一边删掉。可是想了一会儿发现 5 3 9 1 的情况会把
3
3
3 的两条链全都删掉,看来贪心不太对。
然后队友看了 I,突然冒出来一堆人通过,于是看了一眼。通过奇妙证明发现,变向不会使得答案变大,于是反过来说变向也不会使得答案变小,于是正反向答案不变。结合大量的通过人数进一步验证,于是从 T T T 出发跑最短路即可。
D 依旧倒闭,三个人都想过了还是不太行。于是看看 C,感觉很贪,一开始想要从小区间扩展到大区间,但是发现 [ 1 , 2 ] , [ 4 , 5 ] , [ 2 , 4 ] [1,2],[4,5],[2,4] [1,2],[4,5],[2,4] 这组数据可以 hack 掉。Zlw 开始发力!一开始又读错题以为 a a a 是给定的,直到看到 1 ≤ n ≤ 1 0 9 1\leq n\leq 10^9 1≤n≤109 才发现又是 a i = i a_i=i ai=i。于是变得非常可做,大部分赋值都会使得答案 − 1 -1 −1。从左到右考虑区间,进一步发现在原本选定的赋值方案后,可以通过在实际上倒着操作来构造合法方案。然后通过各种手玩发现按照 ( r , l ) (r,l) (r,l) 升序排序会比较好处理。问题转化为一个贪心,用 set 分区间维护未删除的点,找到 ≥ l \geq l ≥l 的第一个未删点分配给区间即可。我想了想,感觉很对,于是他又上机写,一发通过!!!!
他俩看了看其它题,D 依旧放着。发现 F 是个好玩的交互,提出了可以一个隔一个的防御,于是 Sky 开始执笔迷题。
至于 D,开局只有队长机能登录,一题题速览,Zlw 看到 D 题题面较短,很快读完发现是个树树题,于是 Zlw 就先到旁边想了,在可以跟榜前没有任何思路,等到发现 G 有人过了就先扔了 D。结果一直到最后卡题的时候才由 Scy 提出了一个神妙贪心,对于一个节点,与下面的节点合并只有三种方式,从头合并,从尾合并以及中间合并。联想到可以分开算贡献,只考虑每一对父亲儿子的贡献即可。但是最后 dp 的时候发现一个后缀和处理错误,以及在考虑两条链合并的时候没有加入其它儿子的贡献,赛时直到最后都没有做出来。
但是写完由于一些神秘的 bug,导致到最后都没过。最后半小时 Sky 还来尝试了 F,但是由于细节太多,这题也没过。最后总排 309,遗憾离场了!
【Scy の补题】
让我们来完整的重新复现一下 D 的思路以及最后的死亡回放:
改完以后就 AC 了,警钟长鸣。
令 d p u , 0 / 1 / 2 dp_{u,0/1/2} dpu,0/1/2 表示 u u u 点放到中间,放到右侧,放到左侧时 u u u 子树内的答案。让我们先来分析一下几种情况。
-
d p u , 1 dp_{u,1} dpu,1 的更新相当于一个原来为向右的箭头, a v a_v av 在最右侧。当 a u > a v a_u > a_v au>av 时,对 d p u , 1 dp_{u,1} dpu,1 的额外的贡献为 a u − a v a_u - a_v au−av,否则为负贡献。
-
d p u , 2 dp_{u,2} dpu,2 的更新同理,其中正的额外贡献为 a v − a u a_v - a_u av−au。若出现负贡献,实际上会在另一种情况中变为正的贡献。
-
d p u , 0 dp_{u,0} dpu,0 稍微复杂一点,分为四种情况:
- → u ← \rightarrow u \leftarrow →u← 且两个箭头不重叠,这一段的贡献更新为 d p k 1 , 1 + d p k 2 , 2 + w k 2 − w k 1 dp_{k1,1} + dp_{k2,2} + w_{k2} - w_{k1} dpk1,1+dpk2,2+wk2−wk1。
- → u ← \rightarrow u \leftarrow →u← 且两个箭头重叠,这一段的贡献更新为 d p k 1 , 1 + d p k 2 , 2 − ( w k 1 − w k 2 ) dp_{k1,1} + dp_{k2,2} -(w_{k1} - w_{k2}) dpk1,1+dpk2,2−(wk1−wk2),减去的就是重叠的那一部分,改为加号其实和第一种情况表达式一致。
- ← u → \leftarrow u \rightarrow ←u→ 且两个箭头是否重叠均可,此时 d p u , 0 dp_{u,0} dpu,0 无法处理贡献,但是该情况会被归类为 d p u , 1 / 2 dp_{u,1/2} dpu,1/2。
综上所述则有
{ d p u , 1 = max k ∈ s o n u { ∑ v ∈ s o n u ∣ v ≠ k max { d p v , 0 , d p v , 1 , d p v , 2 } + d p k , 1 + w u − w v } d p u , 2 = max k ∈ s o n u { ∑ v ∈ s o n u ∣ v ≠ k max { d p v , 0 , d p v , 1 , d p v , 2 } + d p k , 2 + w v − w u } d p u , 0 = max k 1 , k 2 ∈ s o n u ∧ k 1 ≠ k 2 { ∑ v ∈ s o n u ∣ v ≠ k 1 ∧ v ≠ k 2 max { d p v , 0 , d p v , 1 , d p v , 2 } + d p k 1 , 1 + d p k 2 , 2 + w k 2 − w k 1 } \begin{cases} dp_{u,1} = \max \limits_{k \in son_u}\left\{\sum \limits_{v \in son_u \mid v \neq k} \max \{dp_{v,0},dp_{v,1},dp_{v,2}\} + dp_{k,1} + w_u - w_v\right\}\\ dp_{u,2} = \max \limits_{k \in son_u}\left\{\sum \limits_{v \in son_u \mid v \neq k} \max \{dp_{v,0},dp_{v,1},dp_{v,2}\} + dp_{k,2} + w_v - w_u\right\}\\ dp_{u,0} = \max \limits_{k1,k2 \in son_u\wedge k1 \neq k2}\left\{\sum \limits_{v \in son_u \mid v \neq k1 \wedge v \neq k2} \max \{dp_{v,0},dp_{v,1},dp_{v,2}\} + dp_{k1,1} + dp_{k2,2} + w_{k2} - w_{k1}\right\}\\ \end{cases} ⎩ ⎨ ⎧dpu,1=k∈sonumax{v∈sonu∣v=k∑max{dpv,0,dpv,1,dpv,2}+dpk,1+wu−wv}dpu,2=k∈sonumax{v∈sonu∣v=k∑max{dpv,0,dpv,1,dpv,2}+dpk,2+wv−wu}dpu,0=k1,k2∈sonu∧k1=k2max{v∈sonu∣v=k1∧v=k2∑max{dpv,0,dpv,1,dpv,2}+dpk1,1+dpk2,2+wk2−wk1}
对于 d p u , 0 dp_{u,0} dpu,0 的更新,直接做是 O ( n 2 ) O(n^2) O(n2) 的,但是我们可以预处理 d p k 2 + w k 2 dp_{k2} + w_{k2} dpk2+wk2 前后缀最大值,这样就可以在 O ( n ) O(n) O(n) 的时间内更新完。于是这道题做完了,最后时间复杂度为 O ( n ) O(n) O(n),代码如下:
int main ()
{
int n = read ();
vector <int> a (n + 1);
vector <vector <int>> ve (n + 1);
vector <vector<ll> > dp (n+1,vector<ll>(3,0));
for (int i = 1;i <= n;++i) a[i] = read ();
for (int i = 1;i < n;++i)
{
int u = read (),v = read ();
ve[u].push_back (v);ve[v].push_back (u);
}
auto dfs = [&] (auto self,int u,int fa) -> void
{
vector <ll> pre (ve[u].size (),0),suf (ve[u].size (),0);
ll mx1 = -1e18,mx2 = -1e18;int c = 0;
for (auto v : ve[u])
{
if (v == fa) continue;
self (self,v,u);
ll gv = max ({dp[v][0],dp[v][1],dp[v][2]});
mx1 = max (mx1,dp[v][1] + (a[u] - a[v]) - gv);
mx2 = max (mx2,dp[v][2] + (a[v] - a[u]) - gv);
pre[c] = suf[c] = dp[v][2] + a[v] - gv;
dp[u][1] += gv,dp[u][2] += gv,dp[u][0] += gv;
++c;
}
dp[u][1] = max (dp[u][1],dp[u][1] + mx1);
dp[u][2] = max (dp[u][2],dp[u][2] + mx2);
--c;
for (int i = 1;i <= c;++i) pre[i] = max (pre[i],pre[i - 1]);
for (int i = c - 1;i >= 0;--i) suf[i] = max (suf[i],suf[i + 1]);
int cc = 0;ll res = 0;
for (auto v : ve[u])
{
if (v == fa) continue;
ll mx = -1e18,gv = max ({dp[v][0],dp[v][1],dp[v][2]});
if (cc) mx = max (mx,pre[cc - 1]);
if (cc != c) mx = max (mx,suf[cc + 1]);
res= max (res,dp[u][0] + dp[v][1] - a[v] + mx - gv);
++cc;
}
dp[u][0] = res;
};
dfs (dfs,1,0);
printf("%lld\n",max({dp[1][0],dp[1][1],dp[1][2]}));
return 0;
}
【Sky の补题】
题目大意很简单,就是一个棋盘,我先手,一次可以随便下一个位置,然后机器人有一个初始位置,一次可以往八个方向随便走一格,目标就是堵住机器人。
注意到题目给了最大步数限制 T = 1000 T=1000 T=1000,以及机器人最大初始位置 ( 20 , 20 ) (20, 20) (20,20),考虑建一堵横着 30 30 30,竖着 30 30 30 的墙,把机器人围在墙内,然后在里面随便填,最多也就 30 × 30 = 900 30 \times 30=900 30×30=900 步(现在想了下好像都不用 30 30 30 那么远,但赛时为了方便就直接选了 30 30 30)。
我们先手,是个很有用的条件,如何利用好这个条件是解体的关键。当然,开局要先堵 ( 30 , 30 ) (30,30) (30,30),这个其实比较神秘,因为开局不知道机器人怎么走的话,堵其他地方都会浪费。
在草稿纸上玩了半个小时后,发现如果机器人离边界比较远的话,其走的八个方向可以分为四类:
- 左、左下、下。这一类不会威胁我建墙,随便建即可。
- 左上、上。这一类会威胁我建上面的墙,我需要在机器人当前坐标的正上方(顶到 30 30 30)的左边两格建墙。
- 右下、右。这一类会威胁我建右边的墙,同理,我需要在机器人当前坐标的正右方(顶到 30 30 30)的下面两格建墙。
- 右上。这是威胁最大的,同时影响我建上面和右边的墙,所以我记录一个布尔变量 t f tf tf,用于轮流建上面和右边的墙。
当然,如果这种方式需要建的墙被堵住了,在它旁边能建的位置建一个就好了,反正要尽快建墙。
但是,如果机器人走到离边界比较近的地方,具体就是差 2 2 2 格的位置,我们就要考虑结合上面的策略,不要让机器人走出去。
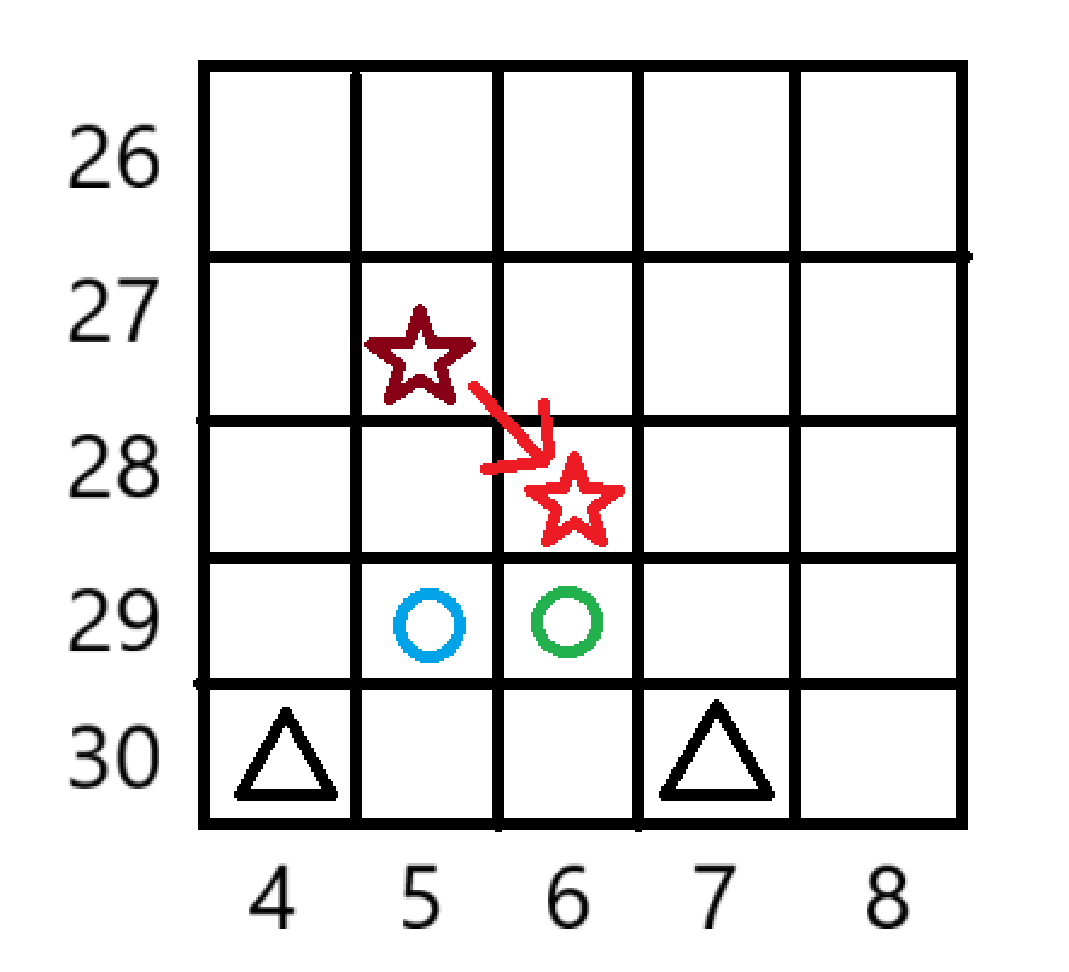
比如上图这种情况,我们的上面的策略其实是可以保证机器人快到边界的时候,不会出现它能到达的五个边界格子 ( 4 , 30 ) , ( 5 , 30 ) , ( 6 , 30 ) , ( 7 , 30 ) , ( 8 , 30 ) (4,30),(5,30),(6,30),(7,30),(8,30) (4,30),(5,30),(6,30),(7,30),(8,30) 有三个连续空缺的情况,这种情况聪明的机器人肯定能走出去。那么假设遇到了上图这种漏洞比较大的情况,我们肯定要优先堵住 ( 6 , 30 ) (6,30) (6,30),然后根据它的移动再去堵下一个。
我们要保证一个事情:机器人离下边界的时候只有 2 2 2 格的时候,它的正下方及周围一共五个格子,必须有至少两个是填上的;以及,机器人离下边界只有一个格子的时候,它的正下方及周围一共三个格子,必须有至少两个是填上的(这个好理解)。
然后墙就建完啦!剩下的就是把机器人围在墙里面,一点一点堵死,感觉机器人应该会很兴奋吧!😋
2025.09.14 The 2025 ICPC Asia East Continent Online Contest (Ⅱ)
C 看了一眼 Zlw 和 Sky 都认为是签到,按照套路先二分,然后尝试贪心分配。发现可以封装一个函数从小到大硬分配每一种题目,然后中间分类讨论如何把前面的东西补到后面然后再用之前那个函数补齐前面,分类讨论少了一点,大概 30 分钟写完。
接下来是 D 题。
【Sky 推柿子】考虑一个子序列的元素被一个一个卖掉所能得到的最大价值是,先将子序列从小到大排序( a 1 a_1 a1 到 a n a_n an),然后从后往前卖,这样后面大的价值可以累积到前面,我们会得到最大价值:
W i = a 1 + a 2 + 2 a 3 + 2 2 a 4 + ⋯ 2 n − 2 a n W_i = a_1 + a_2 + 2 a_3 + 2^2 a_4 + \cdots 2^{n-2} a_n Wi=a1+a2+2a3+22a4+⋯2n−2an
然后我们先将原本给定的序列排序,对于所有子序列,只需要考虑
a
i
a_i
ai 作为子序列的第
j
j
j 个数的贡献。Zlw 佬推了一下式子发现总的答案就是
W
=
∑
i
=
1
n
(
∑
j
=
2
i
(
i
−
1
j
−
1
)
⋅
2
j
−
2
⋅
2
n
−
i
+
2
n
−
i
)
=
∑
i
=
1
n
2
n
−
i
(
∑
j
=
2
i
(
i
−
1
j
−
1
)
⋅
2
j
−
2
+
1
)
=
∑
i
=
1
n
2
n
−
i
⋅
(
3
i
−
1
−
1
2
+
1
)
=
∑
i
=
1
n
2
n
−
i
⋅
3
i
−
1
−
1
2
\begin{align} W &= \sum_{i=1}^n \left( \sum_{j=2}^i \binom{i - 1}{j - 1} \cdot 2^{j-2} \cdot 2^{n-i} + 2^{n-i} \right) \\\ &= \sum_{i=1}^n 2^{n-i} \left( \sum_{j=2}^i \binom{i - 1}{j - 1} \cdot 2^{j-2} + 1 \right) \\\ &= \sum_{i=1}^n 2^{n-i} \cdot \left( \frac{3^{i-1}-1}{2}+1 \right) \\\ &= \sum_{i=1}^n 2^{n-i} \cdot \frac{3^{i-1}-1}{2} \end{align}
W =i=1∑n(j=2∑i(j−1i−1)⋅2j−2⋅2n−i+2n−i)=i=1∑n2n−i(j=2∑i(j−1i−1)⋅2j−2+1)=i=1∑n2n−i⋅(23i−1−1+1)=i=1∑n2n−i⋅23i−1−1
这里要注意两个细节:
-
一个是最大价值序列的系数并不是一个 2 i 2^i 2i 的序列,其第一项和第二项都是 1 1 1,在计算答案的时候要处理一下。
-
第二个就是二项式定理,要确保不算错。
【Zlw 推柿子】尝试计算 a i a_i ai 在最终答案中的出现次数。可以枚举 a i a_i ai 在答案中的排名 r r r,相同 a i a_i ai 约束为按原序列的顺序即可。得到:
f i = [ ∑ i = 2 r ( r − 1 i − 1 ) 2 n − r × 2 i − 2 ] + 2 n − r = 2 n − r × ( ∑ i = 0 r − 1 ( ( r − 1 i ) 2 i − 1 ) − 1 2 ) + 1 ) = 2 n − r 3 r − 1 + 1 2 f_i=[\sum_{i=2}^{r} \binom{r-1}{i-1}2^{n-r}\times 2^{i-2}]+2^{n-r}=2^{n-r}\times(\sum_{i=0}^{r-1}(\binom{r-1}{i}2^{i-1})-\frac{1}{2})+1)=2^{n-r}\frac{3^{r-1}+1}{2} fi=[i=2∑r(i−1r−1)2n−r×2i−2]+2n−r=2n−r×(i=0∑r−1((ir−1)2i−1)−21)+1)=2n−r23r−1+1
然后乘上系数加起来即可。
我在看 E,看着 n , m n,m n,m 均为 1 0 9 10^9 109 的数据产生了疑问,趁着空机的时候敲了暴力 dfs。很快就发现 n n n 为奇数的时候答案为 ( 2 m − 1 ) n − 1 (2^m - 1)^{n - 1} (2m−1)n−1,但是偶数的时候没发现规律。Zlw 看了一眼奇数的答案然后尝试猜测含义, n − 1 n - 1 n−1 个数随便填,然后用最后一个数去修正。偶数似乎会遇到相邻重复的问题。于是我灵光一现,尝试用奇数规律的答案和正确答案作差,还真给我找到规律了!偶数时候的答案为 ( 2 m − 1 ) n − 1 + ( − 1 ) n 2 × ( 2 m − 1 ) n 2 (2^m - 1)^{n - 1} + (-1)^{\frac{n}{2}} \times (2^m - 1)^{\frac{n}{2}} (2m−1)n−1+(−1)2n×(2m−1)2n。哦,还要特判 n = 2 n = 2 n=2 时答案为 0 0 0。于是乎这题被我猜完了,提交一发通过。
H 题 Zlw 看了很久终于看懂题了,然后发现其实可以强制链头链尾改变,然后算每个长度的链有多少条就可以。但是感觉思路很简单,跟树没什么关系,然后中间清空写挂了一个 corner case 一直没发现,红温了很久。还贡献了两罚时 + 40 min 思考时间(这也导致我们比另外一个队罚时多了 2 min)。
I 题 Zlw 开局有点看错题,以为可以直接问 ( 1 , n , 1 ) (1,n,1) (1,n,1),后来发现询问出来的式子形如 z f 1 + z 2 f 2 + z 3 f + ⋯ + z n − 1 f n − 1 zf_1+z^2f_2+z^3f_+ \cdots +z^{n-1}f_{n-1} zf1+z2f2+z3f+⋯+zn−1fn−1,但是并未想打拉格朗日插值,只想到也许可以高斯消元。Sky 尝试根据图上的情况寻找方案但是失败了,于是 Sky 去和 Scy 看计算几何去了。从高斯消元的思路出发,尝试通过 n − 1 n-1 n−1 次询问特殊的 z z z 从而能够 n 2 n^2 n2 消元。最终在系数矩阵上发现了规律,由于最终只关心最后一个式子的结果,可以计算从 n − 1 n-1 n−1 个式子凑最后给定式子的值,于是可以把矩阵旋转求 n − 1 n-1 n−1 个系数。此时的矩阵第 i i i 列形如 a ⃗ = [ a i , a i 2 , a i 3 , ⋯ , a i n − 1 ] \vec a=[a_i,a_i^2,a_i^3,\cdots,a_i^{n-1}] a=[ai,ai2,ai3,⋯,ain−1],令第 j j j 行式子为 f j f_j fj,对每个 i i i 做差分 f j ← f j − a i × f i − 1 f_j\leftarrow f_j-a_i\times f_{i-1} fj←fj−ai×fi−1 即可消出上三角矩阵,每一项呈现下降幂的形式。如果询问 1 1 1 到 n − 1 n-1 n−1 则会使得上三角的 a i , j = A ( j , i ) a_{i,j}=A(j,i) ai,j=A(j,i)。然后对上三角直接消元即可 n 2 n^2 n2 得到系数了。
但是赛时写错了 A n m A^m_n Anm 的公式,找 Sky 验证还说没问题,以为真没问题。以及差分的时候每次只用差分 n − i + 1 n-i+1 n−i+1 项,结果我全部差分了,后面数组还搞错了一个地方。但是沙比交互库 WA 返回 RE,最后时间紧只测了一个手搓的样例,以为只是哪里不小心 RE 了一直疯狂提交直到发现是感叹号之后 RE 了,一直没有认真调试,以后交互题不能相信交互库返回的结果。
A 题其实不难,但是因为是计算几何,一开始就直接跳过了,最后一个小时才开始认真看,结果最后因为一点点小细节没有 AC。
题目大意是给定 z z z 平面上几个点,每个点都可能有半径为 R 2 R_2 R2 的误差,然后有个半径为 R 3 R_3 R3 的球体小鸟,中心在 z z z 平面上,可以在给的几个点之间随便游走,求小鸟游走可能最大的凸包体积。
稍微画几个图就会发现其实就是,直接先求原来几个点的平面凸包,然后凸包最外围延申 R 2 R_2 R2 的长度,端点处就是圆形平滑曲线。样例给的图挺好的。然后到三维就是刚才这个围起来的曲线边缘变成半径为 R 3 R_3 R3 的半球形,高度为 2 R 3 2R_3 2R3 的立体图形。样例如下图所示,就是求这玩意的体积:
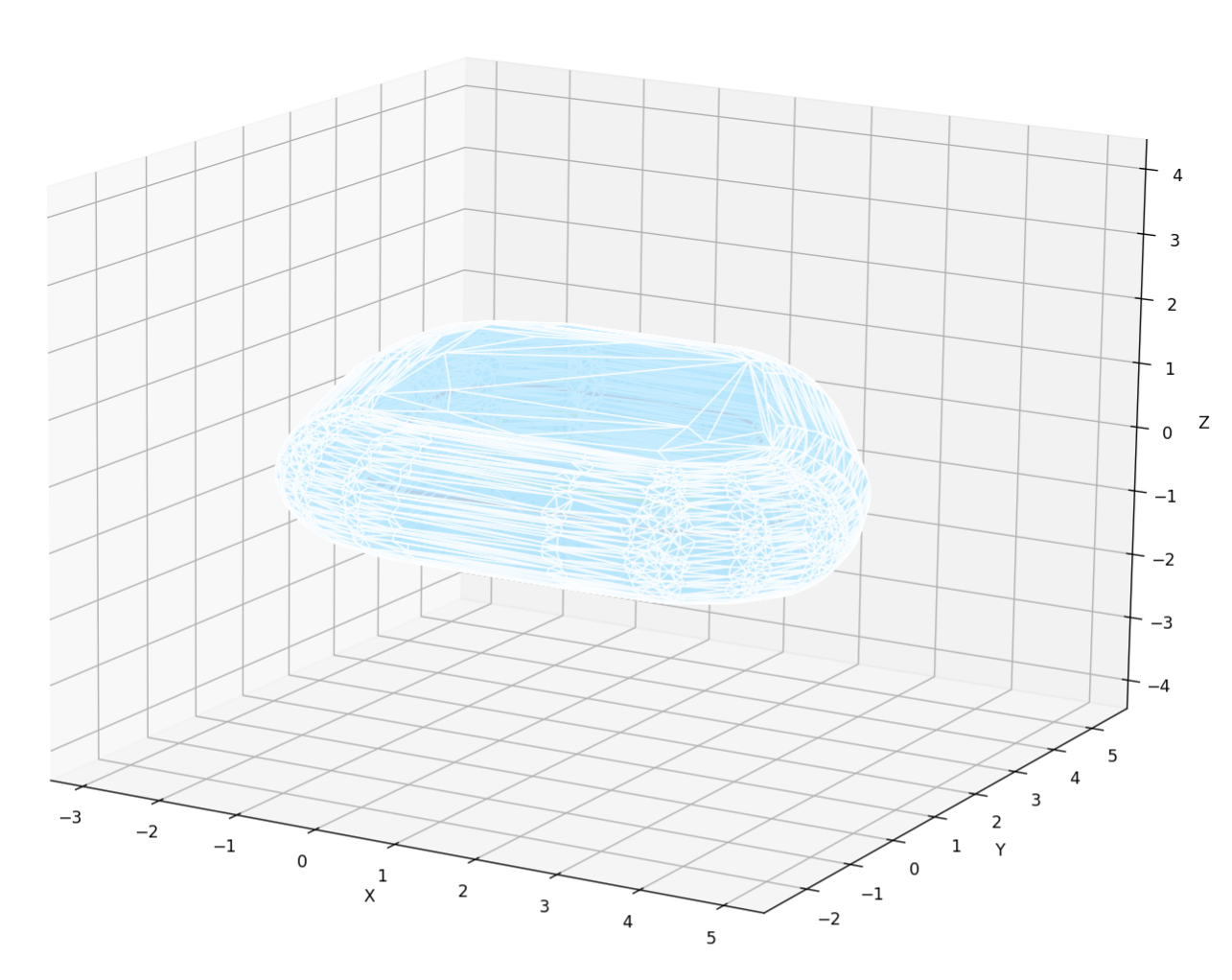
赛时 Sky 已经通过切割,将这个图形大致分成三个部分:中心的柱体、周围直线边和圆角。其中中心柱体和直线边都很好算,简单的体积公式就能算出来,但是,在计算圆角的体积的时候出现了严重问题。
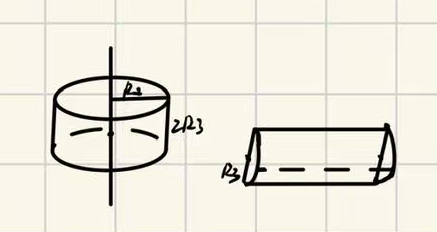
Sky 和 Scy 当时简单地将圆角又切成了上面两个立体图形,一个标准圆柱体和一个半圆柱体,想当然地认为圆角体积和就是:
V 1 = 2 π R 2 2 R 3 + π 2 R 2 R 3 2 V_1 = 2 \pi R_2^2 R_3 + \pi^2 R_2 R_3^2 V1=2πR22R3+π2R2R32
导致赛时最后十分钟连样例都没过,而且就差一点。那么这个式子错在哪呢,难道圆角不能这么切割吗?还真是。
赛后 Sky 用积分重新算了一遍,先记:
R
=
R
2
+
R
3
2
−
z
2
f
(
z
)
=
S
=
π
R
2
R = R_2 + \sqrt{R_3^2 - z^2} \\\ f(z) = S = \pi R^2
R=R2+R32−z2 f(z)=S=πR2
然后体积就是
V
2
=
2
∫
0
R
3
f
(
z
)
d
z
=
2
∫
0
R
3
(
π
R
2
2
+
π
R
3
2
−
π
z
2
+
2
π
R
2
R
3
2
−
z
2
)
d
z
=
2
π
R
2
2
R
3
+
π
2
R
2
R
3
2
+
4
3
π
R
3
3
\begin{align} V_2 &= 2 \int_0^{R_3} f(z) dz \\\ &= 2 \int_0^{R_3} (\pi R_2^2 + \pi R_3^2 - \pi z^2 + 2 \pi R_2 \sqrt{R_3^2 - z^2}) dz \\\ &= 2 \pi R_2^2 R_3 + \pi^2 R_2 R_3^2 + \frac{4}{3} \pi R_3^3 \end{align}
V2 =2∫0R3f(z)dz=2∫0R3(πR22+πR32−πz2+2πR2R32−z2)dz=2πR22R3+π2R2R32+34πR33
会发现 V 2 V_2 V2 比上面的 V 1 V_1 V1 多了一个 4 3 π R 3 3 \frac{4}{3} \pi R_3^3 34πR33,即一个半径为 R 3 R_3 R3 的球的体积,就是鸟本身,到底哪里多出来了一只鸟??
其实就是切割圆角的问题,我们将圆柱周围一圈展开的时候,是不能直接用右边那个半圆柱的体积去算的,因为这个半圆柱是压缩过的,我们要考虑内半径和外半径长度不同,也就是说周围这一圈是不能被展开的,要么用积分算,要么就展开后再把球体的体积加上。
赛后加了鸟的体积之后一发通过。
2025.09.20 第十一届中国大学生程序设计竞赛网络预选赛(CCPC Online 2025)
E 题发现是签到,但是 Sky 一开始有点急,报了一个错误的答案,喜提 20 min 罚时。冷静了一下发现答案应该是 2 ( m − ⌊ n 2 ⌋ ) − 1 2(m - \lfloor\frac{n}{2}\rfloor) - 1 2(m−⌊2n⌋)−1,重新提交后通过。
A 题 Sky 和 Zlw 开了。开局先看错题以为正方形需要横平竖直,看完样例突然傻眼,我一开始认为可以枚举弦图中间的小正方形,然后做八次区间加,复杂度根号但是常数巨大且不好写。然后 Sky 通过约束 4 4 4 个顶点的位置写出了不等式,可以枚举其中一个变量然后直接算另一个变量的区间即可,复杂度根号,可以通过。
我想到一个 G 的做法,于是上机尝试写,写到一半突然发现如果一个数有 n 2 \frac{n}{2} 2n 次,然后询问其它所有数,会直接导致我卡成 n 2 n^2 n2。于是开始进一步手玩 K,试了几个发现倒序输出就是最优的,然后此时答案是 n ( n + 1 ) 2 \frac{n(n + 1)}{2} 2n(n+1),第一 WA 由于数错了导致,重新修正以后通过。
Zlw 来看 G 了,想了一下 Scy 的做法虽然假了,但其实他的做法再根号分治一下就真了。思考后用了传统序列分块,块之间的贡献直接算,块内 O ( B 2 ) O(B^2) O(B2) 预处理,总复杂度 O ( n 1.5 ) O(n^{1.5}) O(n1.5)。
C 题 Sky 先和讨论 Scy 然后提出了一个神奇的贪心。Sky 在转述的时候用了一个比较形象的例子,但 Zlw 认为有点误导题目意思(甩锅)。后来发现本质上是完全图最小生成树,尝试想 B 算法。结合 Sky 的思路本质上是要找连通块外的最小边,与 B 算法极为类似,由于没写过 B 算法,出于正确性的考量,启发式合并存储了每个连通块内的点,用块内点消除全局 multiset 的贡献后寻找最近点,然后并查集合并,迭代了 O ( log n ) O(\log n) O(logn) 层,交上去发现过了。
之后我发现 M 是一个超绝构造就开始想。赛时没有考虑到一些问题导致假掉一直 WA,最后也没过。赛后修补了 bug 但发现需要 > 200 > 200 >200 次,遂倒闭。
首先先对 X X X 求前缀和,每次选取每块的第 i i i 位去加上前一位的值。但有些位置是不需要的,得把影响消除,于是花费额外的 2 × 32 = 64 2 \times 32 = 64 2×32=64 次借助 Y Y Y 做乘法后做减法。之后是块之间的合并,但是仍然要考虑到多余的影响,于是 Y Y Y 先做前缀 max \max max,之后再按照之前的方法先加再消除影响。总共用了 221 221 221 次。发现操作有冗余的地方,但是赛后想了很久都没想出来。
看了一个 Hint 之后直接顿悟。具体如下:
-
先花 32 32 32 次求出每个块内的前缀和(不管 Y Y Y 数组),然后花 32 32 32 次维护块之间的前缀和。即 x i = ∑ j = 0 i x j x_i = \sum \limits_{j=0}^i x_j xi=j=0∑ixj。
-
花费 32 32 32 次做乘法 y i = x i × y i y_i = x_i \times y_i yi=xi×yi,非零位也就变成了无用的位置的前缀和。
-
与 1 1 1 类似,把前缀和改为前缀 max \max max,即 y i = max j = 0 i { y j } y_i = \max \limits_{j=0}^i \{y_j\} yi=j=0maxi{yj}。
-
最后花费 32 32 32 次做减法消除影响, x i = x i − y i x_i = x_i - y_i xi=xi−yi。
好吧确实是个脑瓜题,题目看了很久才懂,然后似乎只有一种解法(?),也就是只有脑电波对上了才可能做出来。然而我并没有脑瓜,也就只能在赛时疯狂 WA 了 qwq。
D 是 Zlw 想出来的, 04 : 57 04:57 04:57 才通过非常极限。想了很久与子序列方案数相关的做法,但是无一例外的会算重,难以维护左端点的合法个数。后来发现随着 r r r 的增加,前面可行的 l l l 在后面可行的 r r r 中一直可行,具有单调性。所以可以直接维护 d p i , j dp_{i,j} dpi,j 表示考虑 [ 1 , i ] [1,i] [1,i],匹配到第 j j j 段且恰好第 j j j 段末尾在 i i i 时,最大的可行的 l l l 在哪。对于首尾无星号,需要维护前缀可行点数;对于单一前面(在后面就翻转)的星号,可以直接产生 d p i , t o t dp_{i,tot} dpi,tot 的贡献;对于前后都有星号,还需要再对 d p dp dp 数组做一次后缀 max \max max,最终极限过题。但是赛后被 Scy 叉了,原因是没特判无星号的情况,而恰好数据没有无星号的情况。
9-10 月训练
懒得一一写了,就记录一下情况吧。
- 2025.09.11 The 2nd Universal Cup. Stage 12: Hefei
solved 4/12.
solved 8/14.
solved 6/12.
solved 5/13.
- 2025.10.13 The 2018 ICPC Asia Qingdao Regional Contest
solved 7/13.
- 2025.10.17 The 2024 ICPC Asia Shenyang Regional Contest
solved 3/13.
- 2025.10.19 The 2024 CCPC Shandong Invitational Contest and Provincial Collegiate Programming Contest
solved 8/13.
- 2025.10.23 The 2025 ICPC Asia Xi’an Regional Contest
solved 5/13.
【补题】
- B
题目大意:给定三种颜色的球排成一行,如果相邻两个球的颜色都不一样,则认为这一行是“漂亮的”。现在给定一个串,可以选择 l l l 和 r r r,使得区间 [ l , r ] [l,r] [l,r] 的所有球随便换位置,能否使得其变成“漂亮的”,求最短区间的 l l l 和 r r r 以及变成的“漂亮的”区间的解。
看到 n ≤ 2 ⋅ 1 0 6 n \leq 2 \cdot 10^6 n≤2⋅106,和 l , r l, r l,r,考虑能否固定一个 l l l 然后二分 r r r。通过观察可知,假设要随意调整一个固定的区间 [ l , r ] [l, r] [l,r],且 L = l − 1 , R = r + 1 L=l-1, R=r+1 L=l−1,R=r+1(区间的左右边),假设最多的颜色数量为 A A A,其次为 B B B 和 C C C,可以分成六种情况:
- A = B = C A = B = C A=B=C,肯定有解
- A = B > C A = B > C A=B>C,如果 L L L 和 R R R 颜色相同且等于 B B B 的颜色,交换 A B AB AB 并做下面的步骤
- A > B > C A > B > C A>B>C 且 A > B + C + 1 A > B+C+1 A>B+C+1,无解
- A > B > C A > B > C A>B>C 且 A = B + C + 1 A = B+C+1 A=B+C+1, L L L 和 R R R 的颜色要都与 A A A 的不同才有解,否则无解
- A > B > C A > B > C A>B>C 且 A = B + C A = B+C A=B+C,只要 L L L 和 R R R 的颜色有一个与 A A A 的不同即可,否则无解
- A > B > C A > B > C A>B>C 且 A < B + C A < B+C A<B+C,肯定有解
这样就可以 O ( 1 ) O(1) O(1) check 啦!然后得到最小答案区间 [ l , r ] [l, r] [l,r] 之后还要找到专这样的区间,考虑枚举这个区间每一位可以放什么,比如枚举 i i i 放 A A A 后,再用上面的二分 check [ i + 1 , r ] [i+1, r] [i+1,r] 是否合法即可。
这题比较有意思的是其单调性,我们枚举 l l l 的范围是左边第一个到第一次出现颜色重复的位置,二分 r r r 的范围是右边第一次出现重复的位置到右边最后一个,这样找出来的“美丽的”区间,其加上左右本身就是“美丽的”部分,还是一个“美丽的”区间,而其稍微缩小一点就会导致“不美丽”,想到这个单调性之后剩下的 check 和还原就比较顺了,分类讨论和模拟稍微有点小细节。
- K
考虑标题"killing bits",可以发现 a i → b i a_i \rightarrow b_i ai→bi 的必要条件之一是 b i ⊂ a i b_i\subset a_i bi⊂ai。然后需要通过操作消除多余的位数。
然后还需要考虑强制保留 b i b_i bi 存在的位。因此与 b i b_i bi 匹配的排列中的元素 p i p_i pi 必须满足 b i ⊂ p i b_i\subset p_i bi⊂pi。
优化一下第二个条件的建图跑匹配就过了。暂时不会证如何满足第一个条件。
- M
赛时是观察到 1 1 1 的重要性,以及 n n n 为奇数时全 1 1 1 序列的不合法性。可是在一些其它情况中,没有想清楚到底哪些序列会因 1 1 1 的双消而留下最后一个数,导致序列不合法。
这个题的策略是尽可能的消成 1 1 1 并放置到两侧,后来打了一个暴力表,看哪些情况是不合法的。一看表就发现规律了。
当序列中的数,满足下列情况中的一条即为不合法序列:
- n n n 为奇数且全为 1 1 1
- 序列中的数 a i a_i ai 均满足 a i ≥ n ∨ ( a i = 1 ∧ 1 < i < n ∧ ∄ i ∈ [ 2 , n − 1 ] , s.t. a i − 1 = a i = 1 ) a_i \ge n \vee (a_i = 1 \land 1 < i < n \land \nexists\ i \in [2,n - 1], \ \text{s.t.}\ a_{i - 1} = a_i = 1) ai≥n∨(ai=1∧1<i<n∧∄ i∈[2,n−1], s.t. ai−1=ai=1)
发现这个结论以后直接写 DP 记录不合法序列的个数即可,一发通过。
- 2025.10.26 The 2025 ICPC Asia Chengdu Regional Contest
solved 6/13.
【补题】
- D
是个码量大的模拟记搜 DP,可能因为脑子不太清醒,反正赛时一个多小时没调过。赛后发现有个地方少敲了变量累加,以及忘记斯诺克最后要按顺序击打彩球了。
- K
CKM 似乎是一个难度的,由于赛时被 A,D 两题恶心了,所以没来得及做,有点点可惜,不过实操下来思路简单,代码难写。
题意:给定 n n n 个定长 L L L 的线段,可以移动恰好一个线段到任意非负位置,求恰好有 k k k 个线段的位置最多有多少个。
考虑枚举移动的线段,分为两种形式:移动到与之前完全不交的区间、移动到与之前相交的区间。
考虑每次移动只影响区间内部 k − 1 , k , k + 1 k-1,k,k+1 k−1,k,k+1 的位置,前缀和维护是可行的,尝试将一些变量分离。
第一种情况可以发现区间长度为定值,所以可以只在左端点记录答案,ST 表查询区间 max \max max 即可。
第二种情况非常恶心,反正各推了一个有八项的式子,兜兜转转能够分别写成 t l − 1 ( 1 ) − t l − x ( 1 ) , t l + x ( 2 ) − t l − 1 ( 2 ) t^{(1)}_{l-1}-t^{(1)}_{l-x},t^{(2)}_{l+x}-t^{(2)}_{l-1} tl−1(1)−tl−x(1),tl+x(2)−tl−1(2) 的形式, t t t 同样是用左端点存区间答案的形式,然后最终 ST 表查某个区间的 max \max max。需要注意 x x x 的值域以及 t ( 1 ) t^{(1)} t(1) 和 t ( 2 ) t^{(2)} t(2) 会有些许不同。
- 2025.11.05 The 2022 ICPC Asia Nanjing Regional Contest
solved 7/13.
出征 XCPC
2025.11.01-11.02 ICPC 武汉站
2025.11.08-11.09 ICPC 南京站
2025.11.29-11.30 CCPC 重庆站
两个佬都有自己的博客😭
出线 EC Final (?)
2025.11.23 上海站的结束意味着大陆所有赛站的结束,看了俊杰的 EC Final 出线预测,似乎拿到了正式的 228 支正式队伍名额的一个(看预测武汉和南京的都可以出线,非常意外,本来以为要靠学校的 WF 奖励名额了)。





















 305
305

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








