INS/GNSS组合导航（四）卡尔曼滤波比较之KF/EKF/UKF/PF

原创已于 2023-06-14 11:18:04 修改 · 8.5k 阅读

94 ·

CC 4.0 BY-SA版权

文章标签：

#自动驾驶 #扩展卡尔曼滤波

于 2022-04-30 21:30:22 首次发布

INS/GNSS组合导航专栏收录该内容

18 篇文章

订阅专栏

本文深入探讨卡尔曼滤波及其进化版EKF、UKF和PF的差异。卡尔曼滤波是线性系统的高效滤波器，而EKF通过泰勒展开处理非线性，UKF利用无迹变换避免线性化误差，适用于高度非线性系统。粒子滤波则采用蒙特卡罗方法，能处理非高斯分布，但计算复杂度高。每种滤波器在不同场景下各有优劣，选择依赖于系统特性和需求。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.摘要

卡尔曼滤波自1960年代发表至今，在各个时间序列估计领域尤其是位置估计、惯性导航等得到了广泛的应用，后续逐渐演化出EKF、UKF以及PF，本文重点对比KF、EKF与UKF及PF的差异及演化来历。

2.卡尔曼滤波器由来

卡尔曼滤波（Kalman Filter）是一种高效的自回归滤波器，它能在诸多不确定性情况的组合信息中估计动态系统的状态，是一种强大的且通用性极强的工具。由鲁道夫.E.卡尔曼于1961年前后首次提出，并首先应用于阿波罗计划的轨道预测。卡尔曼滤波器可以视为贝叶斯滤波器的一个特例，为此，可以先介绍贝叶斯滤波器，再引出卡尔曼滤波器的概念。

3.贝叶斯滤波器

贝叶斯滤波算法以上一时刻的置信度、当前时刻的控制与观测作为输入，输出当前时刻的置信度。以递推的形式对置信度进行求解。递推便需要初始时刻的状态量，若初始值已知，以该确定值初始化，若该值完全未知，可以均匀分布初始化。

推导贝叶斯滤波算法的过程中，贝叶斯法则是基础，也就是后验概率源于先验概率与似然函数。

3.1贝叶斯滤波器的推导

(1) 设定初值

设定初始 0 时刻状态量随机变量 $X_0$ 的后验概率密度函数：

$f_{X_0}^+(x)$

(2) 预测step：求出先验概率密度函数

$f_{X_k}^-(x)=\int_{-\infty}^{+\infty}f_{Q_k}[x-f(v)]f_{X_{k-1}}^+(v)\mathrm{d}v$

(3) 计算似然概率密度函数

$f_{Y_k|X_k}(y_k \ | \ x) = f_{R_k}[y_k-h(x)]$

(4) 更新step：求出后验概率密度函数

$f_{X_k}^+(x)=\eta_k·f_{R_k}[y_k-h(x)]·f_{X_k}^-(x)$

其中，后验概率密度函数中的归一化常数 $\eta_k$ 为：

$\eta_k=\left\{\int_{-\infty}^{+\infty}f_{R_k}[y_k-h(x)]f_{X_k}^-(x)\mathrm{d}x\right\}^{-1}$

(5) 得到状态量的后验估计

 $\hat{x}_k^+=E[f_{X_k}^+(x)]=\int_{-\infty}^{+\infty}xf_{X_k}^+(x)\mathrm{d}x$

3.2 贝叶斯滤波的缺点及解决方法

3.2.1 缺点

从上文的推导及结论中可以发现，求解预测步中的先验概率密度函数 $f_{X_k}^-(x)$ 、更新步中的归一化常数 $\eta_k$ 、最终的最优估计 $\hat{x}_k$ 时均涉及到无穷积分的计算，这在大多数情况无法得到解析解，使得贝叶斯滤波算法的直接应用十分困难。

3.2.2 解决办法

为了解决贝叶斯滤波中的无穷积分问题，通常从两个角度出发：

(1) 作理想假设

假设状态转移函数 f(x) 和观测函数 h(x) 均为线性函数，过程噪声随机变量 $Q_k$ 和观测噪声随机变量 $R_k$ 均服从0均值的高斯分布——卡尔曼滤波（Kalman Filter）
假设状态转移函数 f(x) 和（或）观测函数 h(x) 为非线性函数，过程噪声随机变量 $Q_k$ 和观测噪声随机变量 $R_k$ 均服从0均值的高斯分布——扩展卡尔曼滤波（Extended Kalman Filter）和无迹卡尔曼滤波（Unscented Kalman Filter）

(2) 化连续为离散

将无穷积分转化为数值积分，一般有以下方法：

高斯积分（不常用）
蒙特卡罗积分（粒子滤波，Particle Filter）
直方图滤波

4.卡尔曼滤波器原理

卡尔曼滤波以贝叶斯滤波为理论基础，同时给出了如下6个前提假设：

(1) 假设一：状态量X服从高斯分布

$X \sim N(\mu_X, \sigma_X^2)$

(2) 假设二：观测量Y服从高斯分布

$Y \sim N(\mu_Y, \sigma_Y^2)$

(3) 假设三：过程噪声Q服从0均值的高斯分布

$Q \sim N(0, \sigma_Q^2)$

(4) 假设四：观测噪声R服从0均值的高斯分布

$R \sim N(0, \sigma_R^2)$

(5) 假设五：状态转移函数为线性函数

卡尔曼滤波模型假设k时刻的真实状态是从（k − 1）时刻的状态演化而来，符合下式：

${\textbf {x}}_{k}={\textbf {F}}_{k}{\textbf {x}}_{k-1}+{\textbf {B}}_{k}{\textbf {u}}_{k}+{\textbf {w}}_{k}$

其中

$\mathbf F_k$ 是作用在 $\mathbf x_{k-1}$ 上的状态变换模型（变换矩阵）。
$\mathbf B_k$ 是作用在控制器向量 $\mathbf u_k$ 上的输入－控制模型。
$\mathbf w_k$ 是过程噪声，并假定其符合均值为零，协方差矩阵为 $\mathbf Q_k$ 的多元正态分布。

${\textbf {w}}_{k}\sim N(0,{\textbf {Q}}_{k})$

(6) 假设六：状态转移函数为线性函数

也就是对于时刻k，对真实状态 $\mathbf x_k$ 的一个观测量 $\mathbf z_k$ 满足下式：

${\textbf {z}}_{k}={\textbf {H}}_{k}{\textbf {x}}_{k}+{\textbf {v}}_{k}$

其中 $\mathbf H_k$ 是观测模型，它把真实状态空间映射成观测空间， $\mathbf v_k$ 是观测噪声，其均值为零，协方差矩阵为 $\mathbf R_k$ ,且服从正态分布。

${\textbf {v}}_{k}\sim N(0,{\textbf {R}}_{k})$

初始状态以及每一时刻的噪声 $\{\mathbf x_0,\mathbf w_1, ...,\mathbf w_k, \mathbf v_1, ...,\mathbf v_k\}$ 都认为是互相独立的，即协方差矩阵非对角元素全部为0。

实际上，很多真实世界的动态系统都并不确切的符合这个模型；但由于卡尔曼滤波器被设计在有噪声的情况下工作，一个近似的符合已经可以使这个滤波器非常有用了，实际应用发现，对于并不完全符合上述模型的动态系统也能得到较好的近似效果。更多其它更复杂的卡尔曼滤波器的变种，在下边讨论中会有具体描述。

5.EKF与UKF到PF

5.1 算法差异推导

5.1.1 从 KF 到 EKF

对于KF，它作为贝叶斯滤波器的一个特例，即这个滤波器是动力学模型和测量模型的一个线性组合。

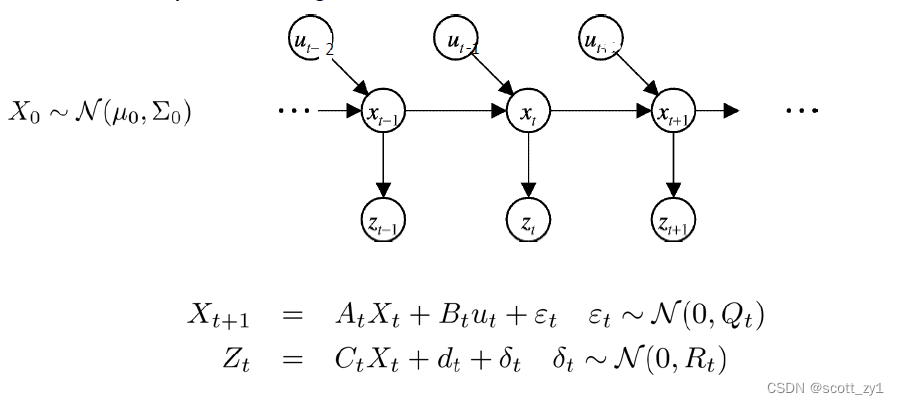
通过上述对比可知，KF模型的状态转移矩阵具有线性化特点，体现在系数矩阵 $A_k,B_k,C_k$ ,

而对于EKF模型来说，状态转移对应下一时刻的状态量是上一时刻的非线性函数，不能直接得到 $A_k,B_k,C_k$ ，需对 $f_k,h_t$ 采用一阶Taylor系列展开式来近似。

5.1.2 从 EKF 到 UKF

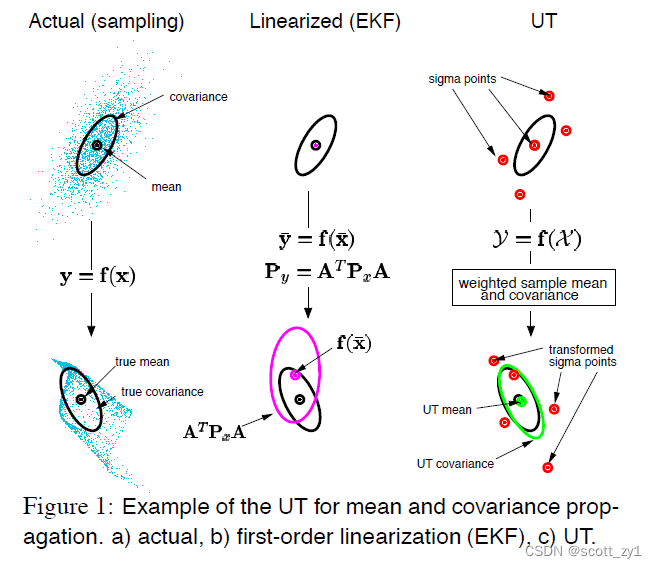
上述EKF中通过非线性函数的一阶Taylor展开式实现线性化，而在UKF则不再采用这种简单的一阶线性化，原因在于对于高度非线性系统，这种舍去二阶以上的线性化处理并不合适，那么从EKF到UKF，最终使得效果好于EKF的直觉在哪里呢？具体可见如下的对比。

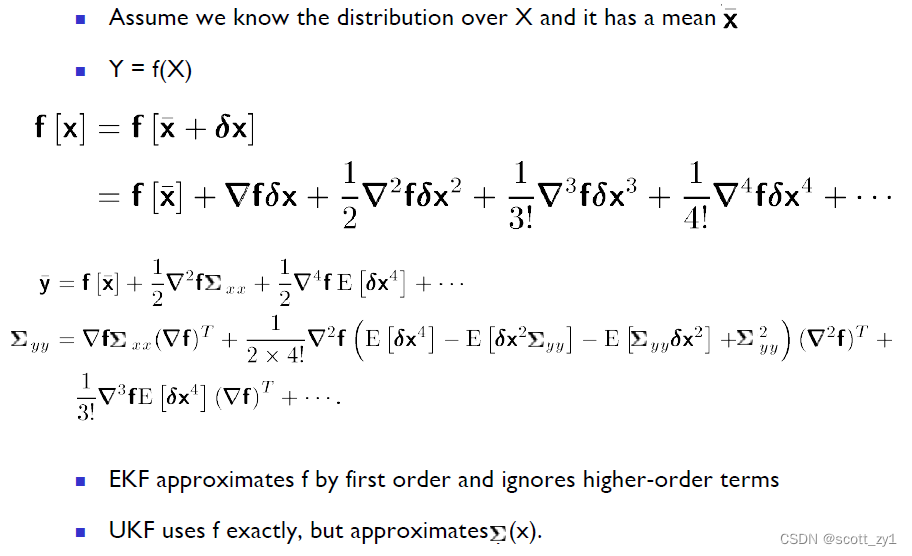
由上可知，在UKF中，不再使用函数的线性近似，而是直接使用了函数本身，但是对函数的自变量 $\mathbf x$ 也就是数据点的协方差进行近似。直观对比EKF与UKF在算法实现上的差异如下:

对于UKF的均值与协方差的更新过程详细步骤如下：

上述详细算法步骤第12步对应的推导过程如下：

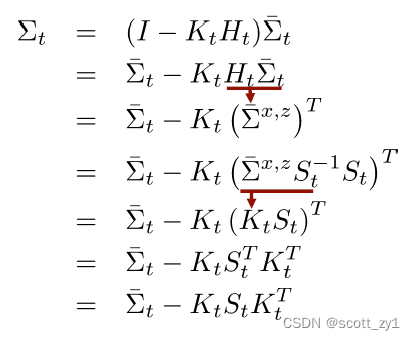
UKF vs. EKF

—— Same results as EKF for linear models
—— Better approximation than EKF for non-linear models

—— Differences often “somewhat small”
—— No Jacobians needed for the UKF
—— Same complexity class
—— Slightly slower than the EKF
—— Still requires Gaussian distributions

5.1.3 从 UKF 到 PF

粒子滤波器（PF：Particle Filter）的思想是基于蒙特卡罗方法，它使用粒子集来表示概率，可以用于任何形式的状态空间模型。核心思想是通过从后验概率中提取随机状态粒子来表达其分布。它是一种顺序重要性采样方法（Sequential Importance Sampling）。

具体来说，引入PF算法，按照如下几个步骤：

a)根据先验概率得到N个初始化粒子。在机器人定位中，粒子的初始分布可设定为均匀分布或高斯分布，协方差矩阵和均值等根据实际情况人为设定。

b)根据机器人的车轮运动速度或者里程对粒子进行状态转移，即将粒子的信息带入机器人的运动模型中，加入控制噪声并产生新的粒子。

c)通过观测模型得到机器人当前的观测位姿。

d)根据观测得到的位姿计算每个粒子的权值。 $W_k(x_k^{(i)})=p(y_k|x_k^{(i)})W_{k-1}(x_{k-1}^{(i)})$ ,其中 $w_k(x_k^{(i)})$ 是k时刻第i个粒子的权值， $w_{k-1}(x_{k-1}^{(i)})$ 是k-1时刻第i个粒子的权值， $p(y_k|x_k^{(i)})$ 是k时刻第i个粒子在这个位置时获得当前观测值的概率。而前一时刻每个粒子的权值在经过重采样之后等于 $1/N$ 。

e)输出滤波结果。对每个粒子加权求和即可。

(f) 根据粒子当前权值进行重采样。重采样的方式有多种，例如系统重采样、多项式重采样、残差重采样、轮盘赌（独立随机重采样）等。

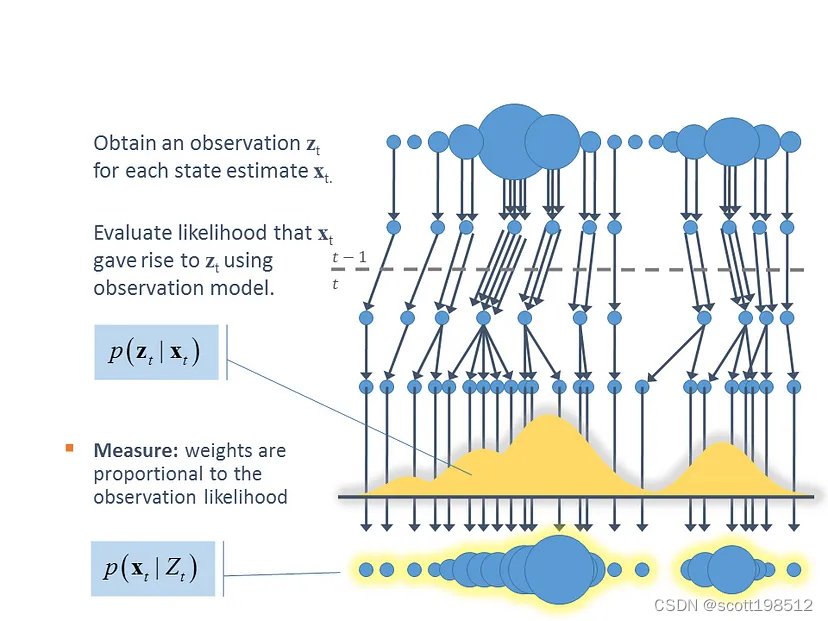
简单来说，粒子滤波法是指通过寻找一组在状态空间中传播的随机样本来逼近概率密度函数，并用样本均值代替积分运算，从而得到状态最小方差分布的过程。

这里的样本指的是粒子，当样本数 $N\rightarrow +\infty$ 时，可以逼近任意形式的概率密度分布。

虽然算法中的概率分布只是对真实分布的近似，但由于非参数的特点，可以摆脱求解非线性滤波问题时随机量必须满足高斯分布的约束，可以表示分布比高斯模型更广泛。它还具有更强的建模可变参数的非线性特性的能力。因此，粒子滤波可以准确地表达基于观测和控制量的后验概率分布，通常可以用来解决SLAM问题。

5.2综合对比

对于KF、EKF、UKF、PF的主要差异，通俗一点说，主要如下：

1）卡尔曼滤波器 KF 是一种用作最小二乘误差优化器的滤波器，为了使其工作，在滤波器内部考虑的系统必须是线性的,即基于线性系统的前提假设。

2）为了使用KF对非线性系统进行状态估计或参数估计，一种可能的方法是围绕其当前状态对正在研究的系统进行线性化，并强制滤波器使用系统的这个线性化版本作为模型. 这是Extended Kalman Filter，或简称为EKF。

3）然而，由于EKF 不是很稳定，而且很多时候，当它确实收敛到“正确”解时，其收敛过程会非常缓慢。为了改进这个滤波器的固有不足，一些作者开始使用 Unscented Transformation，而不是使用线性化来预测被研究系统的行为。因此，具有 Unscented 变换（无迹变换）的 Kalman 滤波器称为 Unscented Kalman Filter，或简称为 UKF。

4）与 EKF 相比，UKF具有一些优势，因为 Unscented 变换在某种程度上比线性化更好地描述了非线性系统，因此该滤波器更迅速地收敛到正确的解。而使用 EKF，这个滤波器可能会变得不稳定，结果可能会出现偏差。

5）UKF没有采用线性化过程，这使得许多人认为它的适用性更广，能够对不可导的函数进行应用，然而实际在许多分段函数模型比如censored measurement model (审查量测模型)中，sigma的选点会导致不连续附近输出的均值和协方差产生偏差，同时初始统计结果也不再适用，进一步会导致结果的发散和有偏。这也就是现在诞生了很多加窗滤波和强跟踪滤波的原因。

6) 相比于UKF，PF即粒子滤波，指通过寻找一组在状态空间传播的随机样本的概率密度函数进行近似，以样本均值代替积分运算，从而获得状态最小方差分布的过程。这种特殊的随机样本就称为“粒子”。PF算法采用这些带有权值的随机样本（特殊样本粒子）来表示所需要的后验概率密度。

7）PF其实是一种蒙特卡罗方法对采样求数值解的过程。这个方法可以求解一般无法通过解析方法求解的方程积分。PF本质上是贝叶斯滤波器采用蒙特卡罗积分后进行数值积分得到的一个特例。

8）相比于KF/EKF/UKF等方法都有高斯分布假设，PF无论计算精度和计算速度都不可与UKF和EKF相比，它更像是为了解决非高斯滤波等假设局限性受制而采取的备选方案。

核心差异总结如下：
KF：线性化假设，求解线性系统，对应的是线性模型
EKF：求解对象是非线性系统，通过Taylor展开式，舍去高阶项，基于线性化思想来近似线性化
UKF：采用线性化近似很多高度非线性系统不合时宜，基于无迹变换，求解得到高斯分布来规避了线性化的行为，UKF的实现具体可分为以下几个步骤：

a) 计算一系列的sigma点

b)给每个sigma点分配一个权重

c)采用非线性变换得到一个点

d根据带权重的点计算一个高斯分布

PF 采用蒙特卡罗积分，适用于非高斯分布。PF属于无参数滤波，它没有具体的后验概率函数，其思路是利用粒子集近似系统的状态分布。所以它可以近似任何系统状态分布。这样的特性，不同于卡尔曼滤波很难实现全局定位，KF/EKF/UKF它主要用于位置追踪。PF则处理全局定位和机器人绑定问题奠定了基础。

PF的主要步骤如下：

1）用运动模型更新粒子集的预测状态。

2）用观测模型计算每个粒子的权重。

3）重采样粒子，使粒子集向权重大的粒子靠拢。

4）用粒子集的均值状态量来表征机器人的状态。

PF的主要问题：a) 粒子退化；b) 粒子枯竭

具体来说，PF算法中采用序贯重要性采样，会出现的一个常见问题就是粒子退化现象，即经过若干次迭代之后，除了少数几个粒子，大部分其他粒子的权值将小到可以忽略不计。粒子退化现象的原因在于，重要性权值的方差将随时间的推移而增加。因此，粒子退化问题的存在意味着大量的计算工作将浪费在更新那些对 $p ( x_k|z^k)$ 几乎为0的粒子上，严重是表现为粒子枯竭。

针对上述粒子退化和枯竭，对应的主要缓解措施：

1）重要性函数的选择

2）重采样

KF、EKF、UKF、PF比较

模型	适用对象	求解方法	计算复杂度/计算速度	应用广泛度
KF	线性系统与线性模型、高斯分布	直接求解	容易/快	较多
EKF	一般非线性系统、高斯分布	Taylor展开式	一般/略慢于KF	最多
UKF	高度非线性系统、高斯分布	无迹变换	复杂/略慢于EKF	很少
PF	高度非线性系统、非高斯分布	蒙特卡罗积分	非常慢	一般