线性回归和代价函数

最新推荐文章于 2025-05-12 15:41:36 发布
原创 最新推荐文章于 2025-05-12 15:41:36 发布 · 2k 阅读 · 11 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#机器学习

目录

1.线性回归算法：监督学习算法的例子

2.代价函数数学定义，有助于弄清楚如何把最有可能的直线与我们的数据相拟合

3.前面给出了代价函数的数学定义，接下来给出例子直观理解代价函数的作用

4.然后我们要讨论有两个参数的情况

1.线性回归算法：监督学习算法的例子

这里还是住房价格的例子，假设你有一个朋友有一个1250平方的房子，想要卖掉，那么根据这个模型，可以用一条直线来拟合，告诉他可以卖到220K，这是监督学习的例子，因为每一个例子有一个“正确答案”。

现在有一个房价的训练集，我们的工作是从这个数据集中学习如何预测房价，下面要定义一些符号：

假设小写字母m表示训练样本的数量，x代表输入变量或特征，y表示输出变量，用（x，y）表示一个训练样本

用他来表示第i个训练样本，上标i只是一个训练集的索引，指的是这个表格中第i行。

学习算法会得出一个假设函数h，而h就是一个引导从x得到y的函数。

函数h的作用是预测y是关于x的线性函数

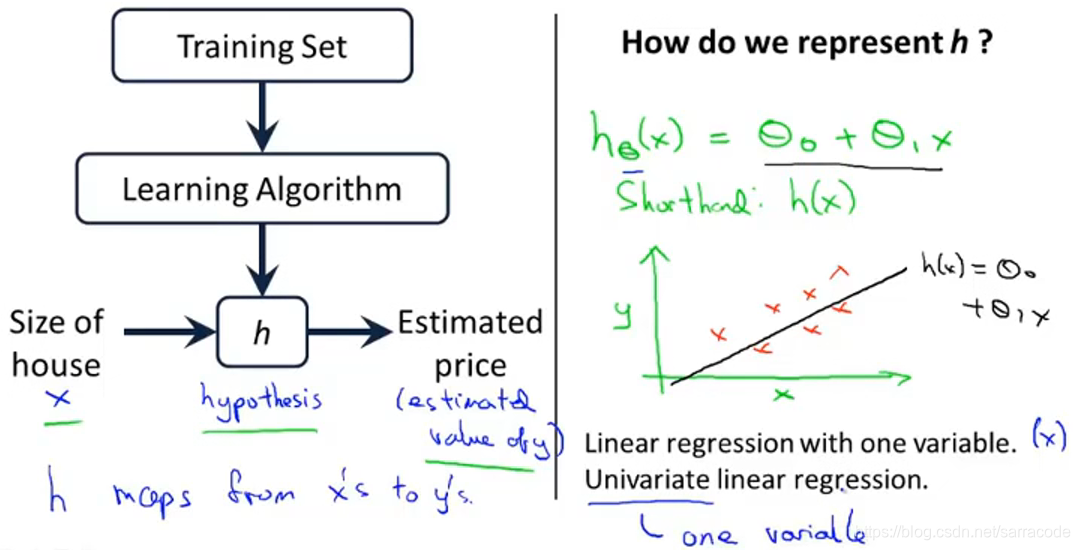
线性函数是学习复杂函数的基础，先拟合线性函数再处理更加复杂的模型

这个模型称为线性回归，这个例子是一个一元线性回归，变量是x，另一个名字是单变量线性回归

2.代价函数数学定义，有助于弄清楚如何把最有可能的直线与我们的数据相拟合

在线性回归中有一个这样的训练集，\Thetai是模型参数，如何选择这两个参数，选择的参数不同的得到的假设函数就不同，如下所示

最低0.47元/天 解锁文章
线性回归(基本概念，代价函数)
2303_78834656的博客
08-12 1765
简单谈谈机器学习中线性回归的相关概念。
线性回归之代价函数除2m
Journey to the West
12-22 6775
线性回归中代价函数为： J=12m∑i=1m(hθ(x(i))−y(i))2J = \frac{1}{{2m}}\sum\limits_{i = 1}^m {{{\left( {{h_\theta }\left( {{x^{\left( i \right)}}} \right) - {y^{\left( i \right)}}} \right)}^2}} 开始为何是除以2m2m，第一反应不应该除以
机器学习-代价函数（单变量线性回归）
小呆苗的博客
04-19 427
机器学习-代价函数（单变量线性回归） 2.1函数表示 因为只含有一个特征/输入变量，所以这样的问题叫作单变量线性回归问题。 回归问题： 构建一个模型，也许是条直线，从这个数据模型上看，如果你朋友的房子是 1250 平方尺大小，能以大约 220000(美元)左右的价格卖掉这个房子，左图就是监督学习算法的一个例子。对于每个数据来说，我们给出了“正确的答案”，即告诉我们： 根据我们的数据来说，房子实际的价格是多少，而且，更具体来说，这是一个回归问题。 分类问题： 当我们想要预测离散的输出值，例如，我们正在寻找癌
机器学习之线性回归与代价函数
weixin_42272869的博客
03-24 1100
线性回归 这个算法会更了解监督学习过程完整的流程 通过一个例子来开始：（根据房屋的大小预测房屋的价格） 这个例子是预测住房价格的，我们要使用一个数据集，数据集包含俄勒冈州波特兰市的住房价格。在这里，我要根据不同房屋尺寸所售出的价格，画出我的数据集。 比方说，如果你朋友的房子是 1250 平方尺大小，你要告诉他们这房子能卖多少钱。那么，你可以做的一件事就是构建一个模型，也许是条直线，从这个数据模型上来看，也许你可以告诉你的朋友，他能以大约 220000(美元)左右的价格卖掉这个房子。这就是监督学习算法的一个例
Machine Learning（Stanford）| 斯坦福大学机器学习笔记--第一周（2.线性回归，代价函数）
MLjoy的博客
08-30 6720
本博客内容来自Coursera上Andrew Ng老师的机器学习课程的。其实一开始在上课的时候我就在本子上做过一遍笔记，这次在博客上再做一遍是对课程的复习巩固，加深印象。--这篇博客的主要内容是介绍了线性回归以及代价函数。
吴恩达机器学习（一）单变量线性回归（假设函数、代价函数、梯度下降）
今天你学习了吗
09-20 4258
目录 0. 前言 1. 假设函数（Hypothesis） 2. 代价函数（Cost Function） 3. 梯度下降（Gradient Descent） 学习完吴恩达老师机器学习课程的单变量线性回归，简单的做个笔记。文中部分描述属于个人消化后的理解，仅供参考。 如果这篇文章对你有一点小小的帮助，请给个关注喔~我会非常开心的~ 0. 前言 单变量线性回归（Linear Regr...
线性回归的代价函数
iot_imx7d_pico的博客
10-09 953
课时七 代价函数 Cost function: 找出最有可能的直线和数据拟合 ≈ 平方误差函数 Hypothesis： hθ(x)=θ0+θ1xh_θ(x) = \theta_0 + \theta_1xhθ​(x)=θ0​+θ1​x θi称为模型参数\theta_i 称为模型参数θi​称为模型参数 Idea:θ0,θ1以便hθ(x)接近训练实例(x,y)Idea: \theta_0, \th...
机器学习---线性回归、多元线性回归、代价函数
weixin_43961909的博客
07-30 1038
训练数据的条目数（＃training set）：一条训练数据是由一对输入数据和输出数据组成的输入数据。根据上一代豌豆的种子（双亲）的尺寸来预测下一代豌豆种子（孩子）的尺寸（身高）。其中，b0是估计线性方程的纵截距，b1是估计线性方程的斜率，y＾是在自变量x等于一个给定值。解决方法：用一条曲线去尽量准的拟合这些数据，然后如果有新的输入过来，我们可以在将曲线上。这个例子的特征是两维的，结果是一维的。如果来了一个新的面积，假设在销售价钱的记录中没有的，怎么处理？该方法处理的数据可以是多维的。这个点对应的值返回。
机器学习笔记（2）- 线性回归模型、代价函数
ygy555的博客
11-05 652
机器学习的线性模型，以及代价函数
机器学习_1.2 （线性回归之代价函数）
qq_42730789的博客
01-30 3327
线性回归 接上一篇的监督学习我们继续深入讨论监督学习中所包含的算法。 给个传送门：机器学习_1.1 言归正传，线性回归问题应该都有基础，用我们所学的简单方程进行运算获得一个函数h(x)用这个函数我们可以很好的对离散型的训练数据进行拟合，这就是机器学习中所谓的线性回归，这篇博客中我们会先从最简单的拟合开始并且逐步深入。 假设函数 中学都学过一次函数，我们假设函数其实也是同理，我们有h(x) = θ2...
线性回归算法、代价函数
柔丽君的博客
11-01 208
参考视频：https://www.bilibili.com/video/BV164411b7dx?p=6&spm_id_from=pageDriver 如何确定 的值： 使输入的x尽量接近对应的y 也就是希望h(x)和y之间的差值尽量小 即（h(x)-y)^2 这个代价函数也被称为平方误差函数 2， ...
线性回归-5-代价函数
哎呦喂的博客
04-02 2296
还记的我们的代价函数吧：J=12∑mi=1(y(i)−θTx(i))2还记的我们的代价函数吧：J=\frac{1}{2}\sum^m_{i=1}(y^{(i)}-\theta^Tx^{(i)})^2现在让我们来看看为什么选择它来作为代价函数。 假设我们的模型如下： y(i)=θTx(i)+ε(i)y^{(i)}=\theta^Tx^{(i)}+ \varepsilon^{(i)} 其中ε(i)
机器学习-线性回归算法（Linear Regression），代价函数(Cost Function),损失函数(Loss Function),梯度下降（Gradient Descent）。
最新发布
2503_91657412的博客
05-12 1096
线性回归是一种基础的机器学习算法，用于预测变量之间的线性关系。本文以房价预测为例，解释了如何通过房屋面积来估算房价，并介绍了线性回归的基本概念。文章详细讲解了如何通过损失函数和代价函数来评估预测的准确性，以及如何使用梯度下降算法来优化模型参数，以最小化预测误差。此外，文章还讨论了学习率对梯度下降过程的影响，强调了适当选择学习率的重要性。整体而言，线性回归通过拟合数据点来揭示变量间的规律，并通过数学方法不断优化预测模型，使其更加准确。本文适合初学者，旨在用简单的语言和例子帮助读者理解线性回归的核心概念。
优化线性回归模型的代价函数
cooldream2009的博客
02-19 1201
线性回归是机器学习领域中最基础的模型之一，它通过找到最佳拟合直线来预测连续型输出变量。在线性回归中，代价函数（Cost Function）起着至关重要的作用，它衡量了模型的性能，并通过优化来调整模型的参数。本文将深入探讨线性回归模型的代价函数及其优化过程。
机器学习（二）：线性回归、代价函数和代价函数可视化
weixin_45733884的博客
02-29 1089
下图为单变量线性回归算法，X是训练集的数据点，f(x)是模型。
机器学习笔记02-线性回归模型中的代价函数与梯度下降
dycljj的博客
11-20 737
总结 该部分主要针对前一节内容进行补充和回顾，上一节主要介绍了-线性回归函数模型与代价函数。上一节内容点此查看。 （1）线性回归函数模型，表示为： hypothesis：hθ(x)=θ0+θ1x等价于：h(x)=θ0+θ1x\begin{array}{l} hypothesis：h_{\theta(x)}=\theta_{0}+\theta_{1} x \\ 等价于：h_{(x)}=\theta_{0}+\theta_{1} x \end{array}hypothesis：hθ(x)​=θ0​+θ1​x等价
Machine Learning第一讲[单变量线性回归] --（一）模型和代价函数
小太阳~
04-08 1192
内容来自Andrew老师课程Machine Learning的第一章内容的Model and Cost Function部分。一、Model Representation1、简单术语 m：训练样本的数目 x：输入变量/特征 y：输出变量/目标变量 ：表示训练集的第i行2、举例： 3、学习算法的工作 h表示hypothesis（假设）4、线性回归拟合曲线 二、Cost Function线
机器学习第一周（线性回归模型与代价函数的数学定义）
PL_hfc的博客
05-25 257
对于房价问题，我们先给出其目标函数θ0θ1minmize\large_{\;θ0​θ1minmize​12m2m1​∑i1m∑i1m​hθxi−yi2hθ​xi−yi2其中，hθxiθ1∗xiθ0hθ​xiθ1​∗xiθ0​θ0θ1minmize\large_{\;θ0​θ1minmize​表示关于θ0和。
机器学习笔记（2）-----单变量线性回归之代价函数
liuhehe123的博客
07-20 1415
线性回归： 表达形式为y = w'x+e，e为误差服从均值为0的正态分布。 线性回归可以分为单变量线性回归(Linear Regression with One Variable)以及多变量线性回归(Linear Regression with Multiple Variables)。在此主要了解单变量线性回归。 以ng课程的房屋交易问题为例：  假设给定一批已知的房子大小和价格的对应...
线性回归代价函数公式
03-25
### 线性回归中的代价函数 在线性回归中，代价函数用于衡量模型预测值与实际值之间的差异。对于单变量线性回归问题，假设 \( h_\theta(x) = \theta_0 + \theta_1x \)[^1] 是模型的预测函数，则其目标是最小化预测值与真实值之间的误差。 具体来说，常用的代价函数（也称为均方误差函数）定义为： \[ J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2 \] 其中： - \( m \) 表示训练样本的数量； - \( x^{(i)} \) 和 \( y^{(i)} \) 分别表示第 \( i \) 个样本的输入特征和对应的实际输出； - \( h_\theta(x^{(i)}) \) 表示模型基于当前参数 \( \theta_0 \) 和 \( \theta_1 \) 对第 \( i \) 个样本的预测值。 该公式的目标是找到合适的参数 \( \theta_0 \) 和 \( \theta_1 \)，使得代价函数 \( J(\theta_0, \theta_1) \) 达到最小值[^3]。这通常通过优化算法（如梯度下降法）实现。 在某些情况下，为了简化计算过程，可能会固定某个参数（例如令 \( b = 0 \) 或者仅调整单一参数），从而将代价函数转化为更简单的形式[^4]。最终，当代价函数达到最小值时，所对应的模型被认为是最佳拟合模型[^5]。 ```python import numpy as np def compute_cost(X, y, theta): """ 计算线性回归的代价函数 参数: X: 输入数据矩阵 (形状为 [m, n]) y: 实际输出向量 (形状为 [m, ]) theta: 当前模型参数 (形状为 [n+1, ]) 返回: cost: 代价函数值 """ m = len(y) predictions = X.dot(theta) errors = predictions - y cost = (1 / (2 * m)) * np.sum(errors ** 2) return cost ``` 上述代码展示了如何根据给定的数据集和模型参数计算代价函数的具体实现方法。 ####
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值