梯度下降法与线性回归算法

目录

梯度下降法

线性回归算法

编程实例训练

矩阵和向量

---

梯度下降法

可以最小化代价函数J，也可以最小化其他函数

给定0，1的初始值，通常都初始化为0,然后同时改变两个参数的值，公式是：

    

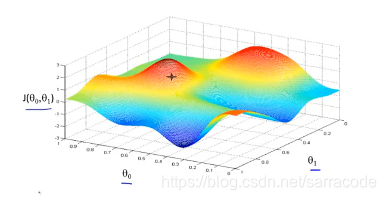
a称为学习率，用来控制梯度下降时，我们迈出多大的步子，如果a值很大，那么梯度下降就很迅速

其中左边的是正确的计算步骤；而右边的是错误的，因为没有做到同步更新，在计算temp1时使用了新的参数值0

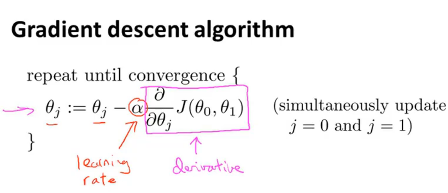
a称为学习速率，它在控制我们以多大的速率改变两个参数的值

第二部分是导数项，那么现在假设只有1个参数，简化式子来讨论导数项的作用如下：

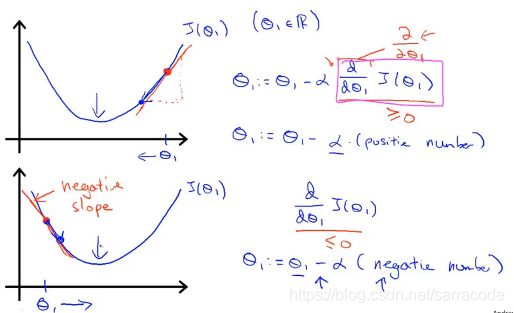
以上面图为例，当取1在最小值的右边时，由于a>0，那么在此处求出导数也为正值，

因此更新1的值相当于1减了一个正数，因此在像最小值靠拢

以下面图为例，当取1在最小值的左边时，由于a>0，那么在此处求出导数为负值，

因此更新1的值相当于1减了一个负数，相当于加了一个数，因此也在像最小值靠拢

接下来讨论学习速率a的作用，如下图所示

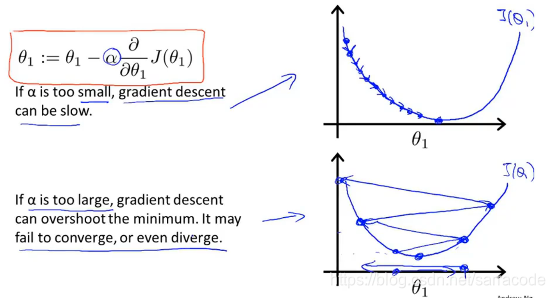
如果a太小，只能迈出一小步，需要很多步才能到最低点，如果a太大，迈出一大步，那么有可能越过最低点，最终导致无法收敛，甚至发散

如果初始时1已经在局部最低点，那么参数值不会改变，始终维持在局部最优点。

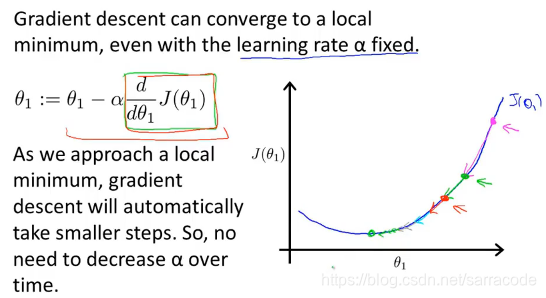
在梯度下降法中，当我们接近局部最低点时，梯度下降法会自动采取更小的幅度，

因为当我们接近局部最低点时，在局部最低时导数等于0，所以当我们接近最低点时，导数值会自动变得越来越小。

 

线性回归算法

在前面我们讲述了梯度下降算法、线性回归模型、平方差代价函数

接下来我们将梯度下降算法和平方差代价函数相结合，得出线性回归算法。

那么我们把梯度下降算法中的导数项展开如下图：

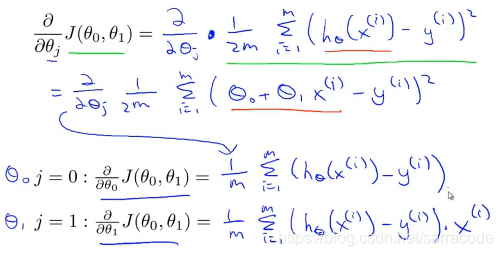
那么整理之后就得到了我们的线性回归算法，如下：

其中需要注意的是我们在使用梯度下降算法时要同时更新这两个参数0和1.

这种线性回归算法有时也称为Batch梯度下降算法，意味着每一步梯度下降，我们都遍历了整个训练集的样本。

编程实例训练

做编程作业Linear Regression 是吴恩达老师的Machine Learning课程中Programming Exercise 1的解题记录

首先ex1是源代码文件夹，里面包含了已经实现好的函数和部分需要自己手动完成的函数

ex1.pdf是对作业的说明文档，其中说明了哪些文件是需要自己手动添加的函数。

那么，在此图中，需要完成的作业内容用星号标记，其他标记则为可选作业

因此，你需要打开这4个函数在需要添加代码的位置处添加代码，然后运行ex1即可，示例其中之一：

打开warmUpExercise.m这个函数，就是在YOUR CODE HERE 处添加代码即可

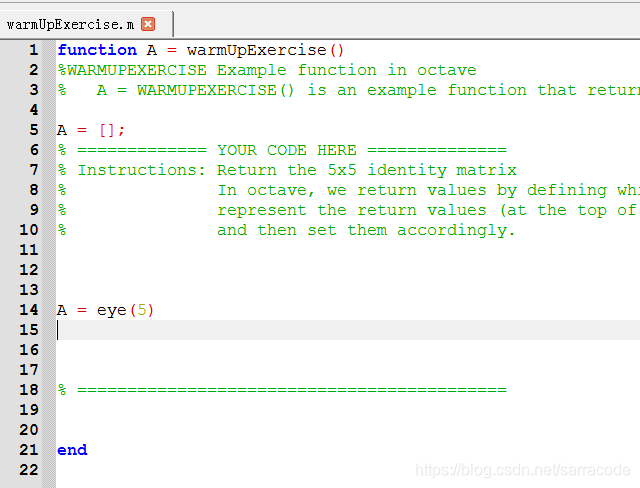
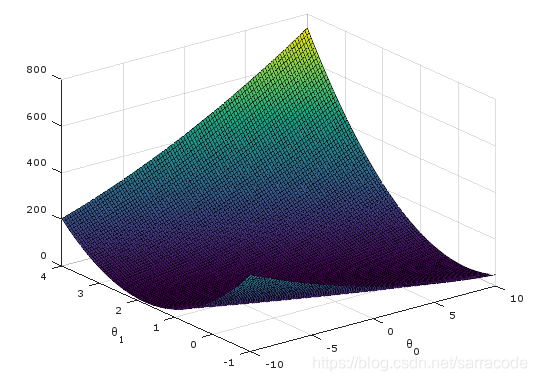
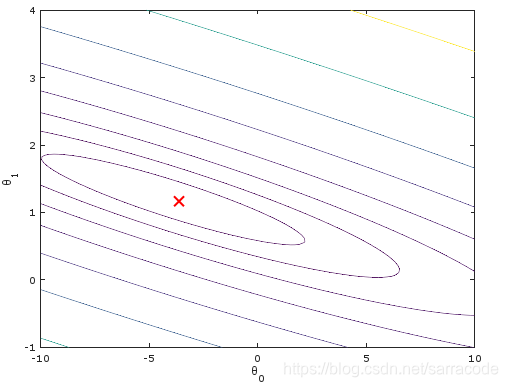
运行结果如下图所示，会得到三张图片：

 

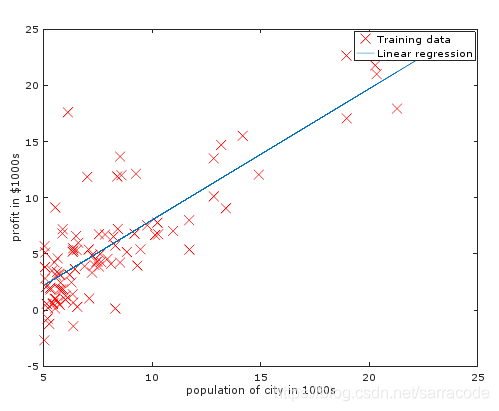
矩阵和向量

向量是只有一列的矩阵即n x 1，通常用大写字母表示矩阵

矩阵加法和标量乘法，标量在这里指一个实数

下面举了一个例子，应用到了前面讲的知识

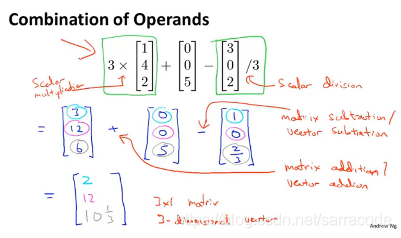
矩阵与向量相乘

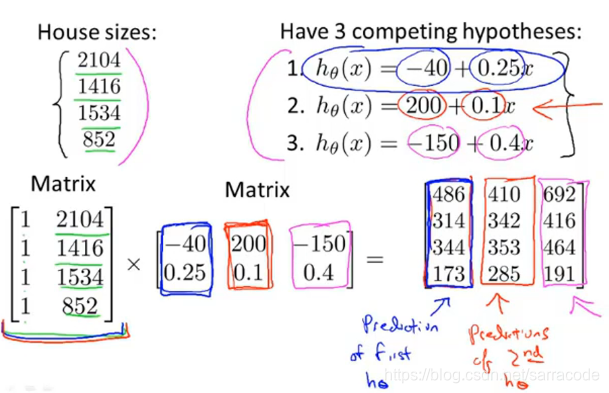
假设有四间房子，大小不同，需要计算每间房子h(x)的值，从而预测他们的价格，可以使用矩阵乘法计算

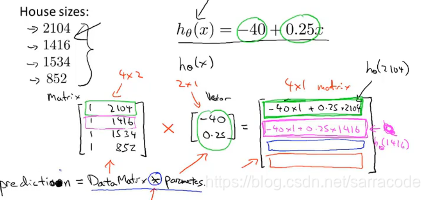
那么在拓展一下可以得到下面的结果：

矩阵乘法不服从交换律

矩阵乘法服从结合律