机器学习算法系列（二十一）-k近邻算法（k-Nearest Neighbor / kNN Algorithm）

最新推荐文章于 2024-09-08 19:50:08 发布

原创

最新推荐文章于 2024-09-08 19:50:08 发布 · 3.4k 阅读

32 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习算法系列 #k近邻算法 #Ball树 #k-d树

本文深入介绍了k近邻（k-NearestNeighbor/kNN）算法，包括模型介绍、距离度量（欧式距离、明可夫斯基距离）、k值选择、决策规则，以及k-d树和Ball树这两种加速查询的结构。通过Python代码展示了kNN分类和回归的实现，并提供了scikit-learn库的使用示例。此外，文章还提供了算法的示例演示和思维导图，帮助读者理解k近邻算法的工作原理和应用。

阅读本文需要的背景知识点：一丢丢编程知识

一、引言

前面一节我们学习了机器学习算法系列（二十）-梯度提升决策树算法（Gradient Boosted Decision Trees / GBDT），是一种集成学习的算法。这一节我们来学习一个相对简单直观的算法——k近邻算法¹（k-Nearest Neighbor / kNN Algorithm）。

二、模型介绍

k近邻算法的思想非常的直观：给定一个新样本点时，只需要在训练集中找到距离最近的 k 个样本点，按照一定的决策规则得到新样本点的预测结果。
如图2-1 所示的分类问题，其中蓝色圆点表示分类为 +1 的样本点，红色叉表示分类为 -1 的样本点，绿色问号表示一个新样本点，当 k = 5 时，即图中绿色虚线圆，包含距离最近的 5 个样本点，其中 3 个为 -1，2 个为 +1，由于 -1 的分类数量多于 +1 的分类数量，则该新样本点的分类被预测为 -1。

图2-1

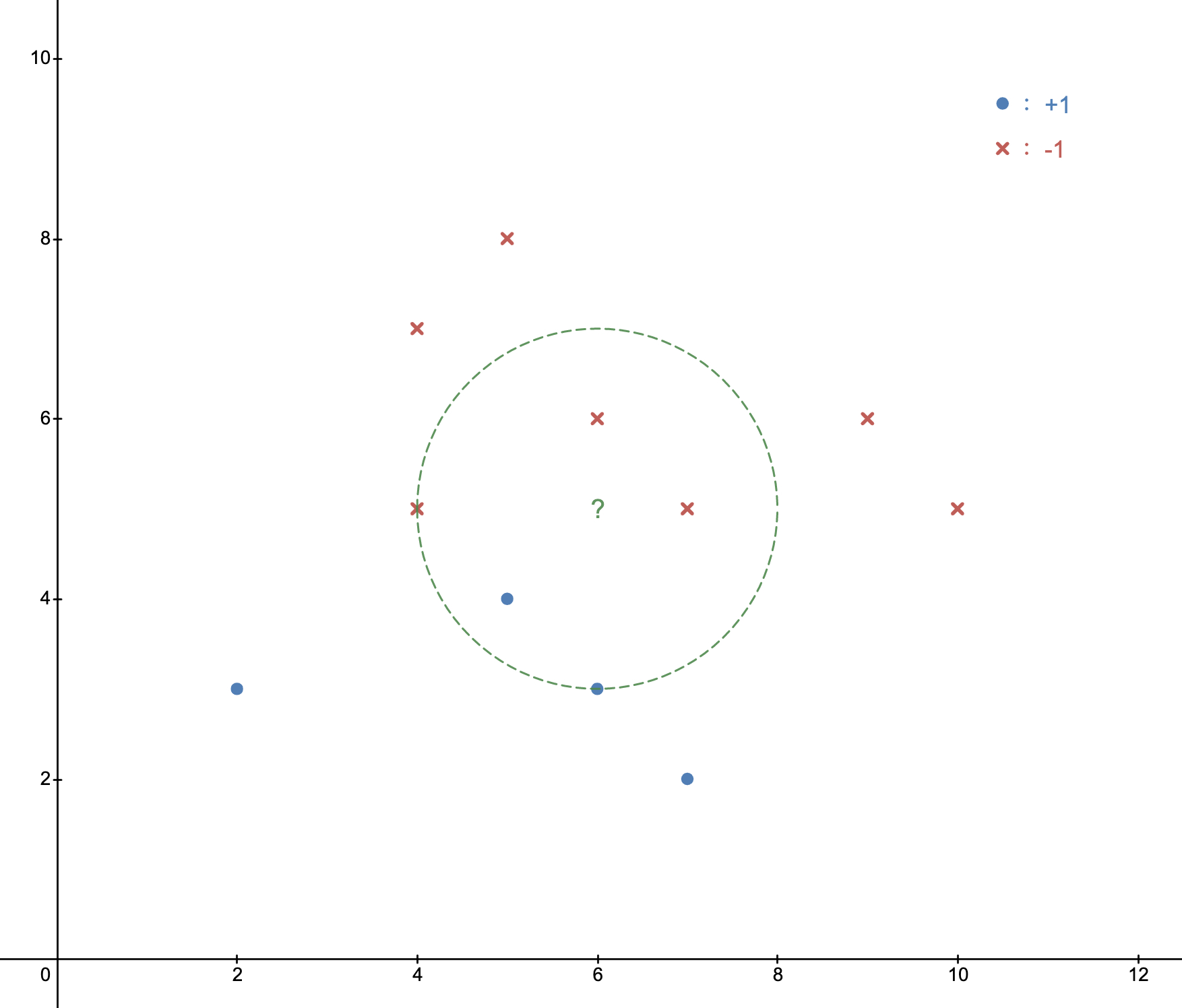
从上面的示例中，我们可以看到整个预测过程由三个基本要点组成，分别是：距离、k 值、决策规则。

距离

既然是近邻，那么如何衡量这个“近”呢？答案自然是通过距离的大小来决定远近，距离的定义中常见的有欧式距离²（Euclidean distance），也被称为 2-范数距离：
$L_2 = \left(\sum_{i = 1}^{n} |x_i - y_i|^2\right)^{\frac{1}{2} }$

式2-1

对于更一般的情况，有明可夫斯基距离³（Minkowski distance），可以看作是欧式距离的一种推广：
$L_p = \left(\sum_{i = 1}^{n} |x_i - y_i|^p\right)^{\frac{1}{p}}$

式2-2

一般算法中默认都是使用欧式距离来作为远近的判断，在 scikit-learn 中可以使用参数 p 来控制距离范数。

k 值

k 值的选取对最后的预测结果有着决定性的影响，当 k 等于 1 时，最后的预测结果只会等同于最近邻居的样本分类，当 k 等于训练集的样本数时，最后的预测结果只会返回训练集中分类占比最大的分类。
由此可以看出，当 k 越小时，意味着模型越复杂，越容易产生过拟合的情况；当 k 越大时，意味着模型越简单，越容易产生欠拟合的情况。一般 k 值会取一个相对较小的值，并通过交叉验证的方式得到一个最优的 k 值。

决策规则

决策规则一般是采用“少数服从多数”的思想。对于分类问题，这 k 个最近的样本中分类最多的类型即为该新样本点的类型；对于回归问题，将这 k 个最近的样本对应的标签值进行平均即为该新样本点的预测值。

三、算法步骤

k 近邻算法

回归

保存训练集
查询最近的 k 个样本点
返回这 k 个样本点的标签平均值

可以看到算法中最核心的方法就是查询最近的 k 个样本点，其中一个最简单的方法就是线型扫描，即遍历整个训练集进行搜索，但当训练集中的样本数过大时，该方式需要对每一个训练样本计算距离，往往过于耗时，这时可以考虑使用一个特殊的结构来存储一开始的训练集，在搜索阶段减少对距离的计算次数，以达到快速检索的目的。

k-维树⁴（k-d tree）

构建 k-d 树

k-d 树是一颗二叉树，按照特征的维度依次进行划分，形成一个超平面，分成两个区域，递归的进行划分，直到无法划分或者区域中包含了指定大小的特征矩阵为止。

图3-1

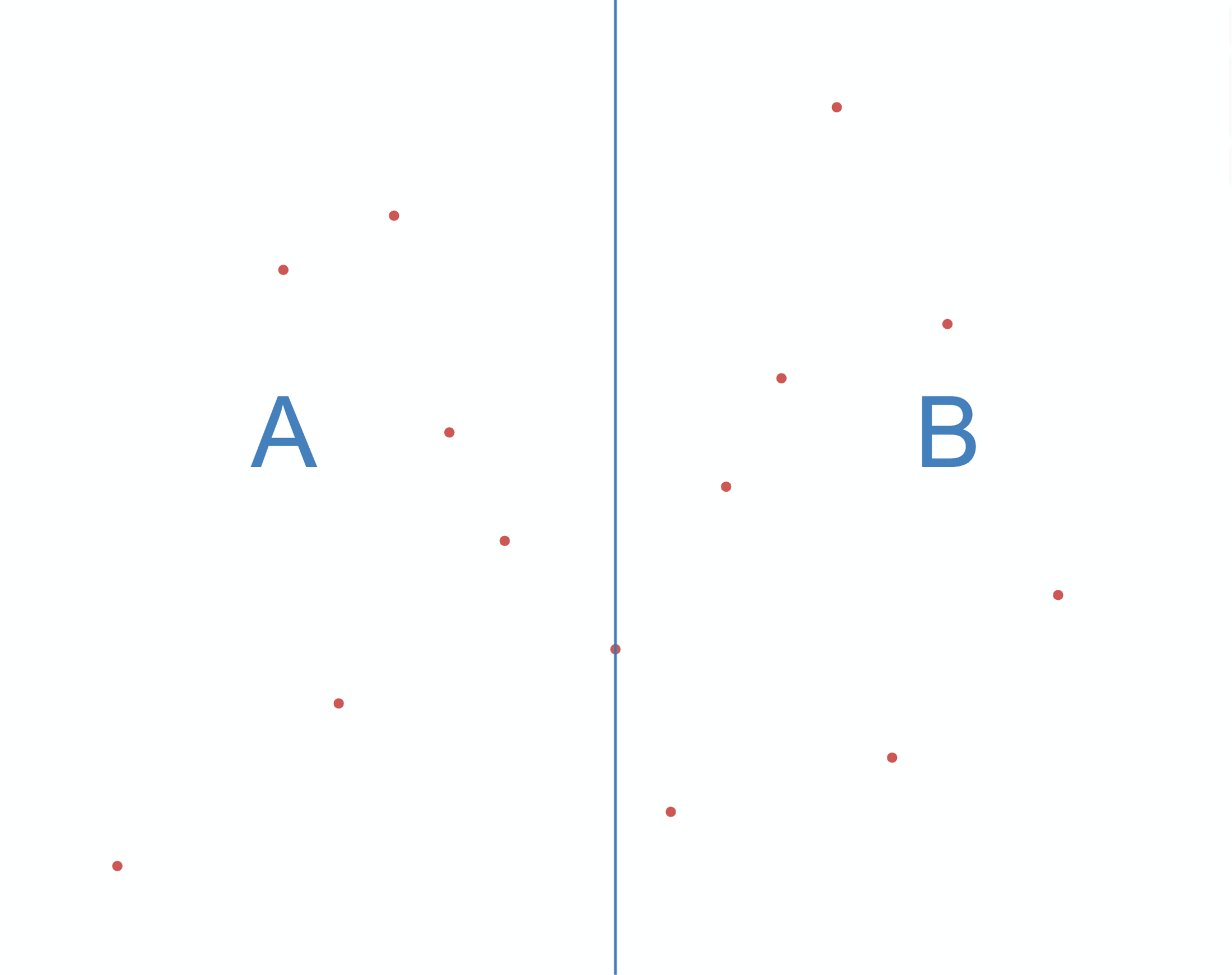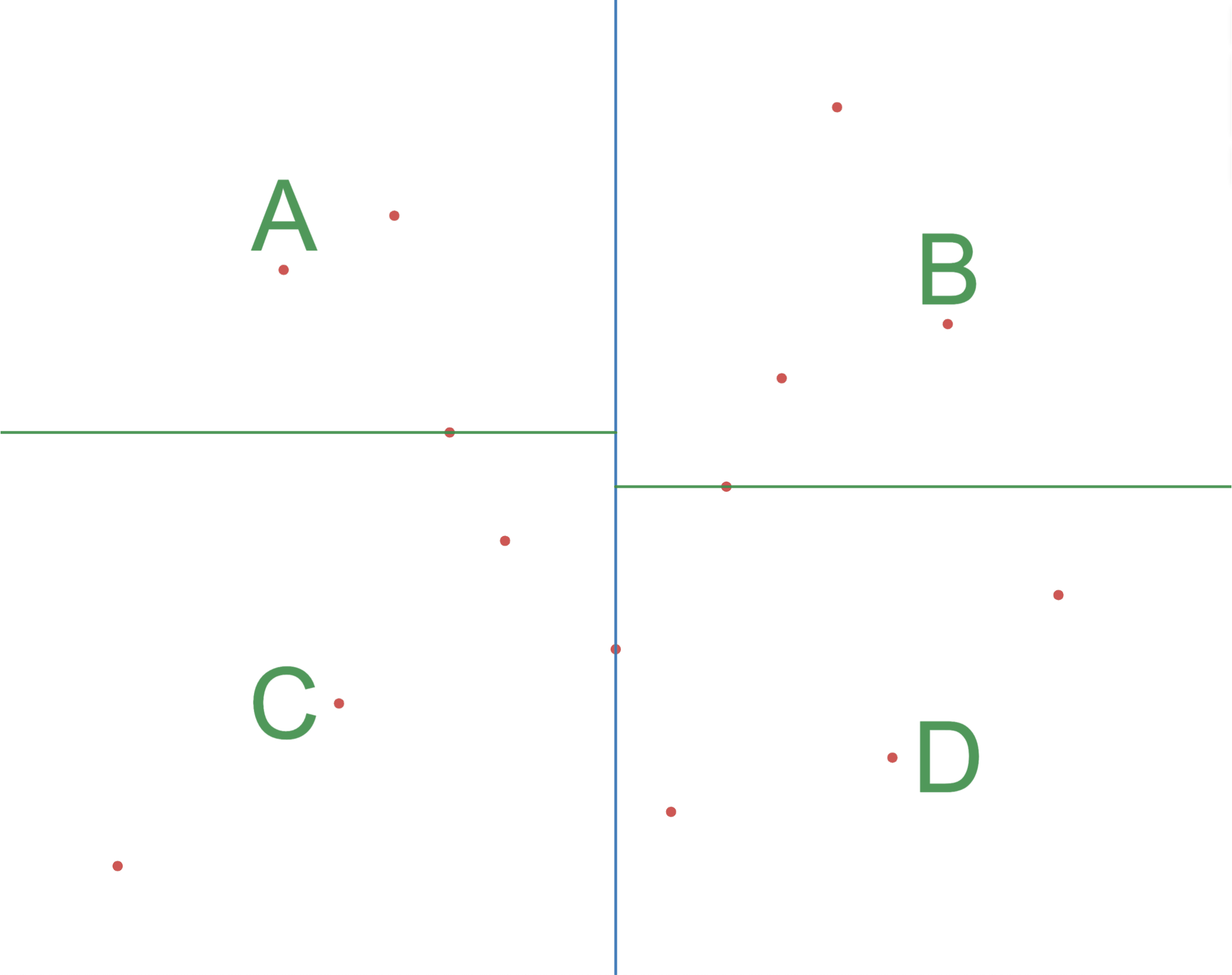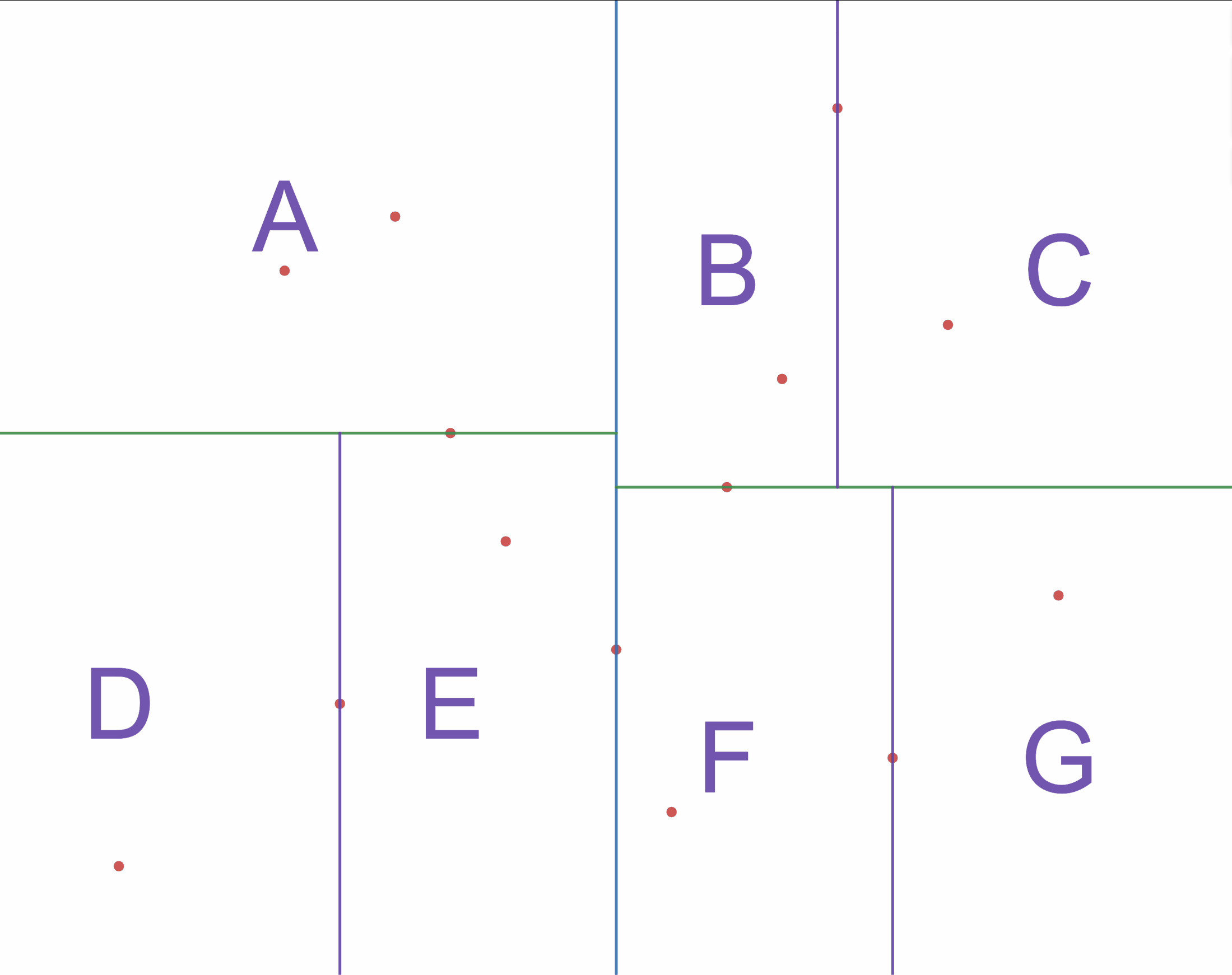
如图3-1 所示，根据一组二维的训练集，构建出一颗 k-d 树，步骤如下：

首先沿着横轴的方向找到该维度的特征值的中位数，垂直于横轴做切分，即图中蓝色竖线，将数据分成了左右两个子区域；
再分别沿着竖轴方向找到左右两个区域在该维度下的特征值的中位数，垂直于竖轴做切分，即图中两条绿色横线；
继续沿着横轴的方向进行切分，得到图中三条紫色的竖线；
这时所有子区域都无法再切分，停止算法；

得到如图3-2所示的 k-d 树

图3-2

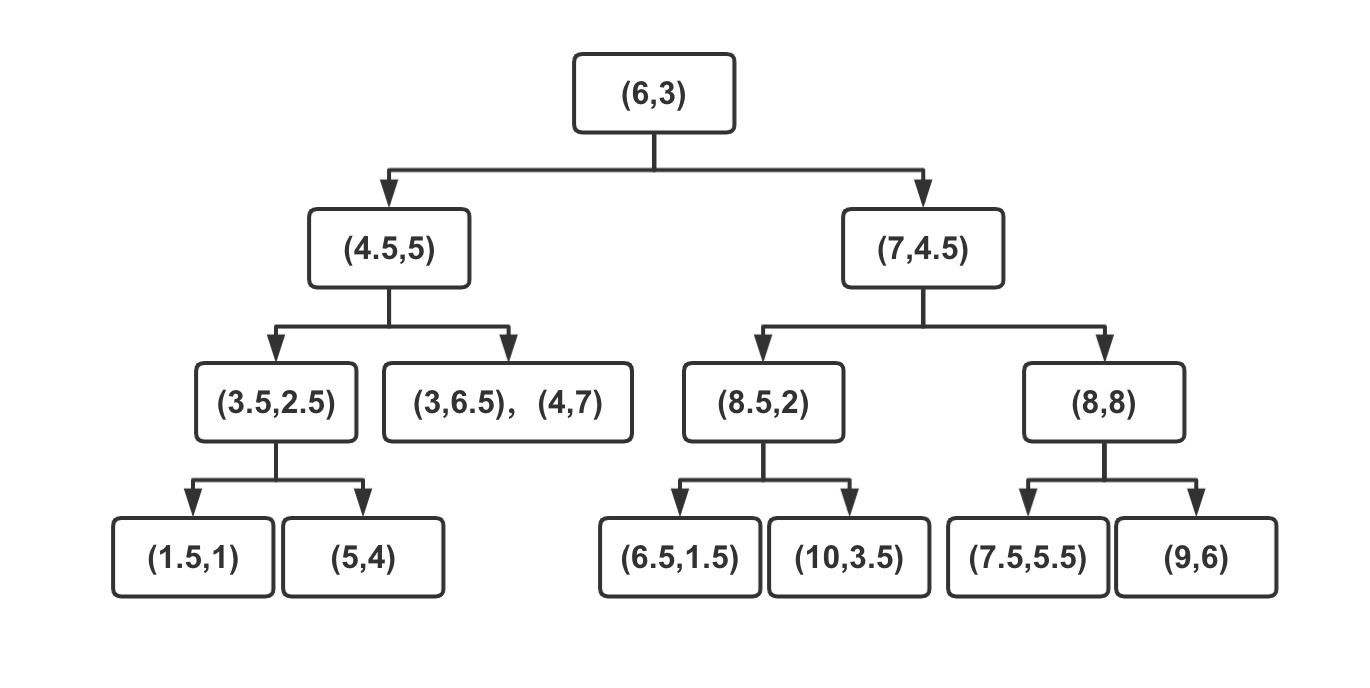
查询 k 近邻

给定一个目标点，查询该点的 k 近邻。只需要搜索包含该目标点的区域和以目标点为圆心，与当前最近点的距离作为半径的圆与超平面相交的区域，相对于线性扫描减少了计算距离的次数。

图3-3

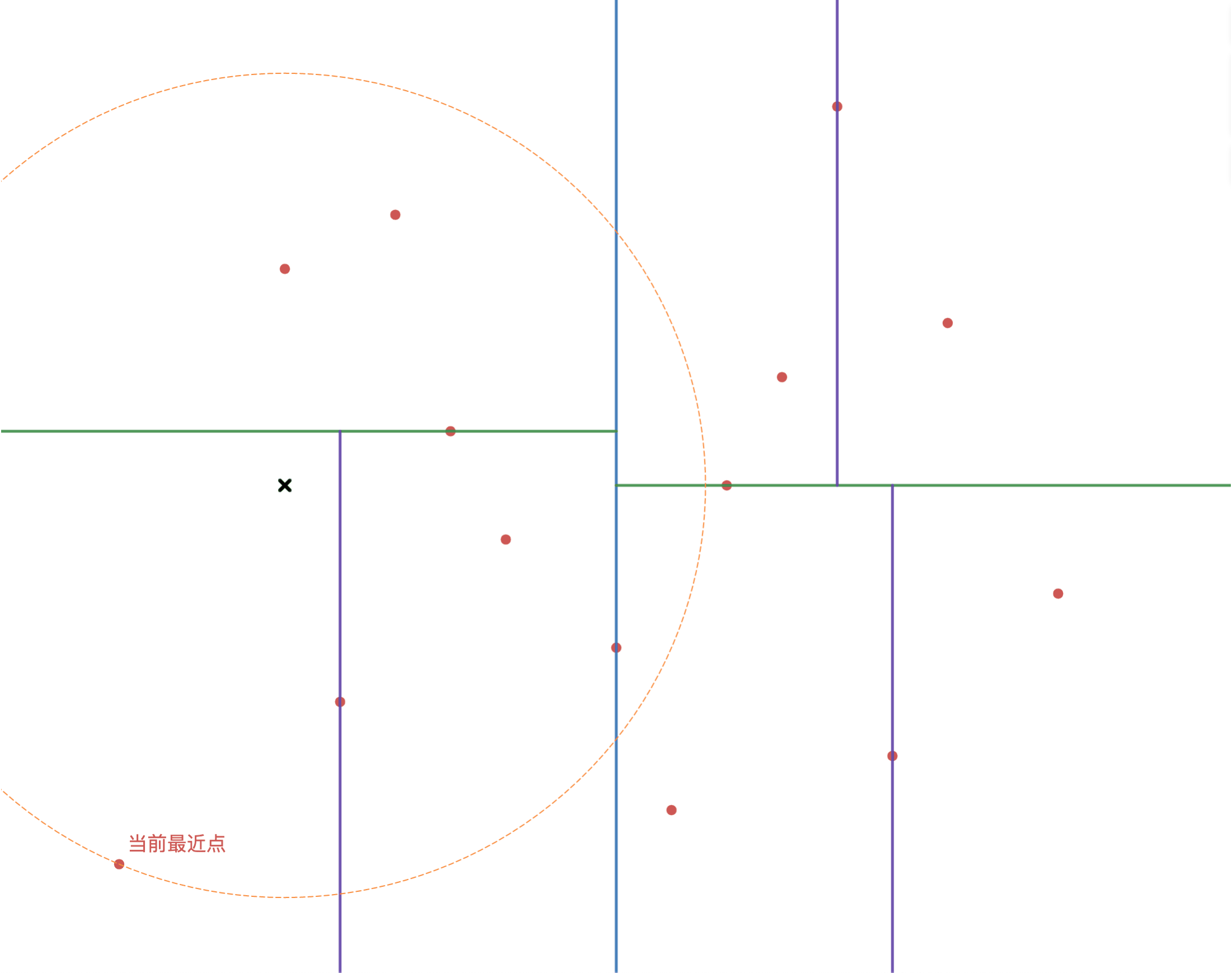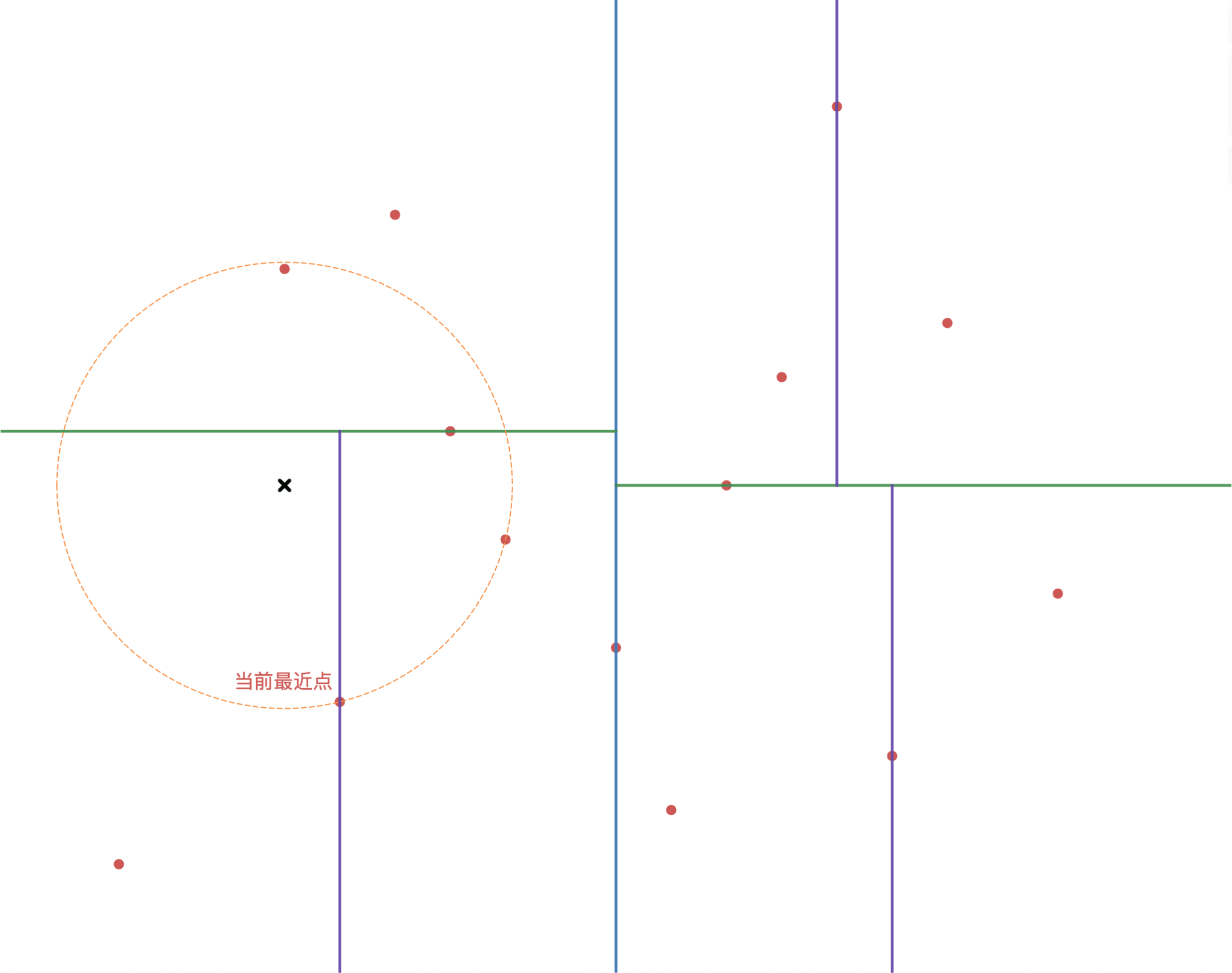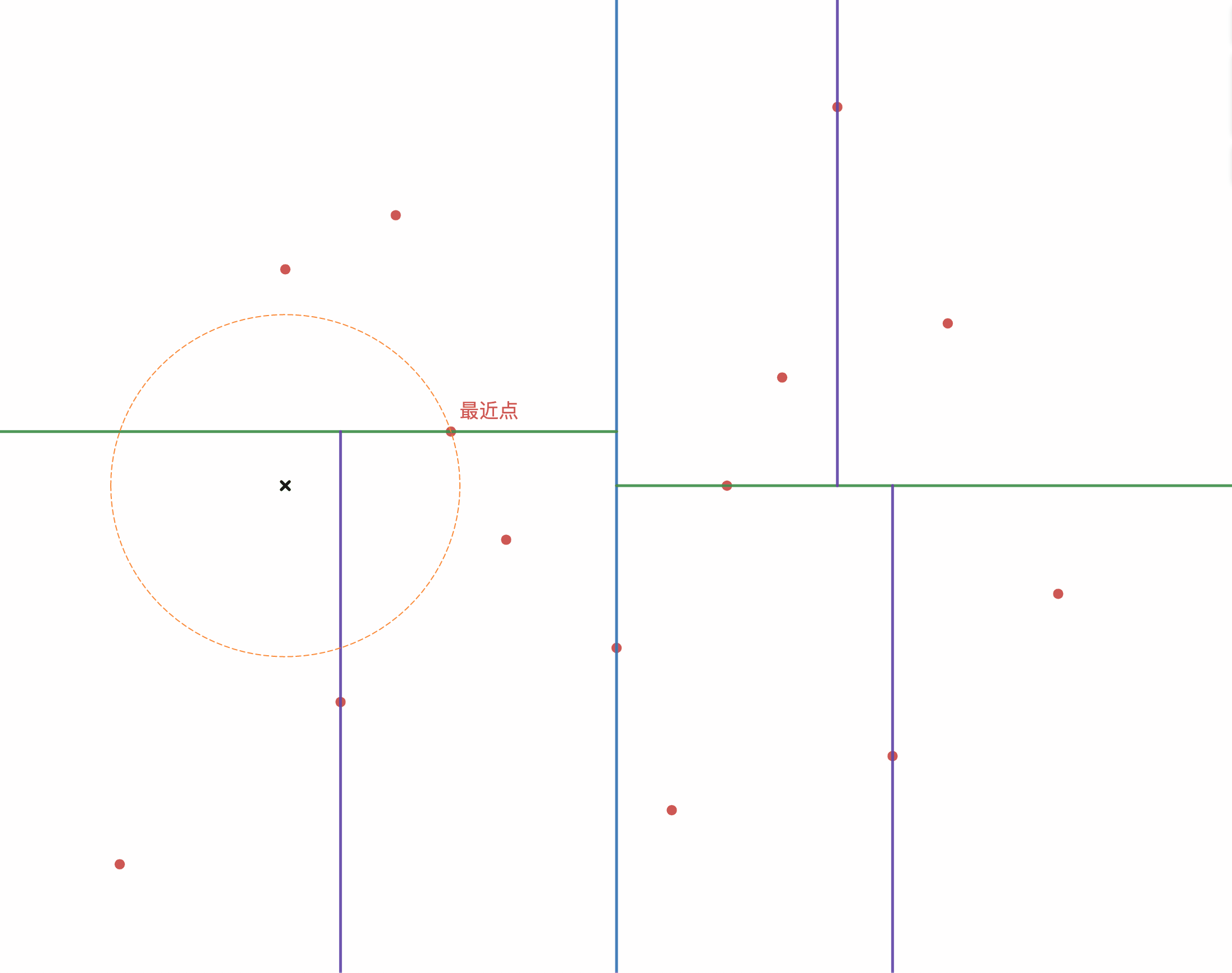
如图3-3 所示，给定一个目标点（图中黑色叉），根据构建出的 k-d 树，进行查询最近邻，步骤如下：

首先从根结点依次向下找到包含目标点区域的叶子结点，即图中左下角的区域；
以当前区域中的点作为当前最近点；
递归的向上查询；
3-1. 检查每一个结点与当前目标点的距离是否小于当前最近点的距离，如果小于则更新当前最近点；
3-2. 检查当前结点的父结点的另一个子结点的区域是否与以目标点为圆心当前最近点之间的距离为半径的圆相交。如果相交，说明可能存在更近点，移动到另一个子结点进行递归搜索；
当搜索到根结点后，结束搜索，当前最近点即为目标点的最近点；

当要搜索 k 个最近点时，只需要按顺序记录即可，算法步骤相同，具体实现可以参考下面的代码实现。

当维度较小时， k-d 树确实能减少查询时计算距离的次数，但是由于树的切分规则是根据维度来做的，当维度过大时，其查询的性能与线性扫描差不多，所以就出现了 Ball 树来解决维度过大时查询的性能问题。

Ball 树⁵（Ball tree）

构建 Ball 树

Ball 树也是一颗二叉树，只是切分的方法不再是按维度来分割，而是每次使用超球面进行切分。

图3-4

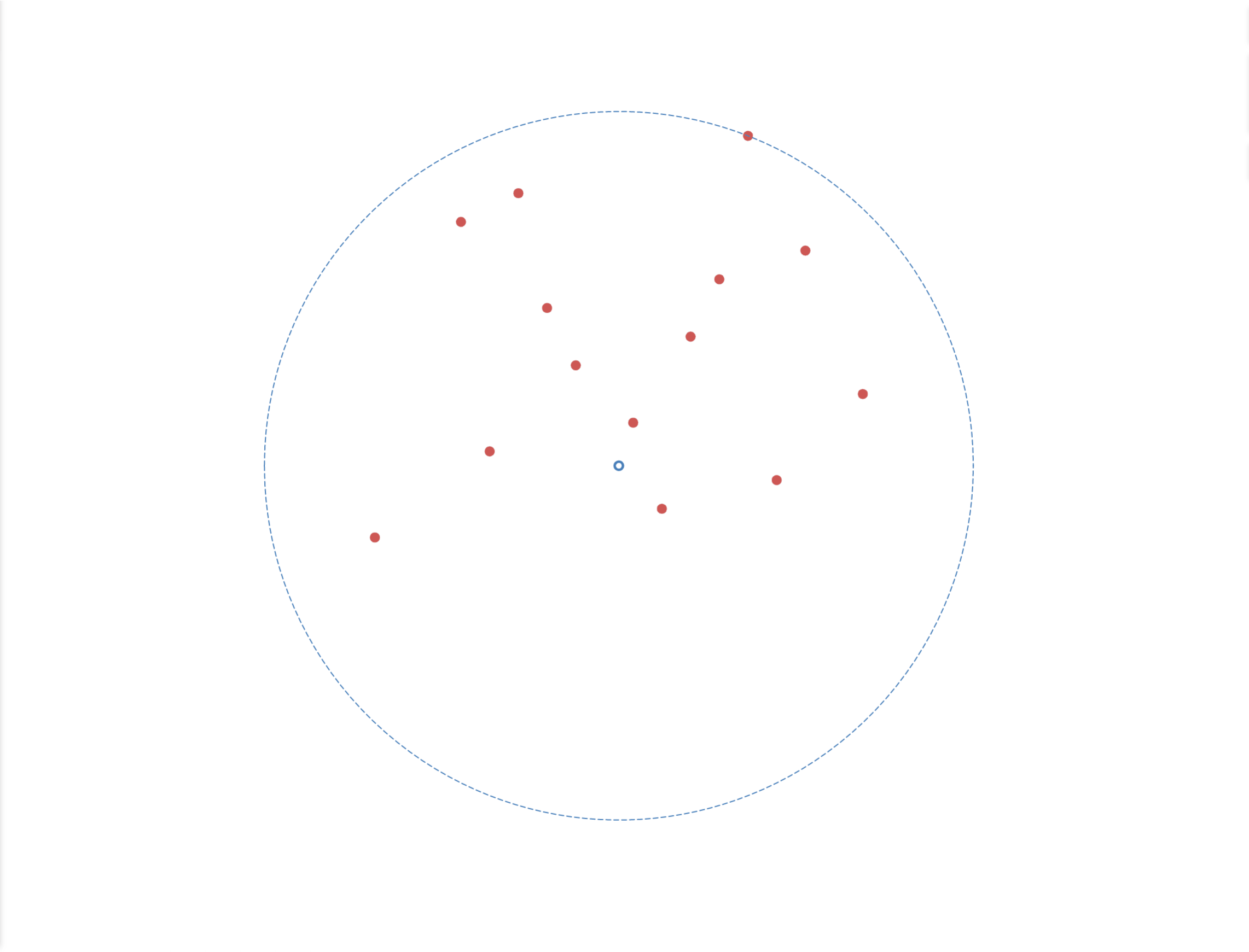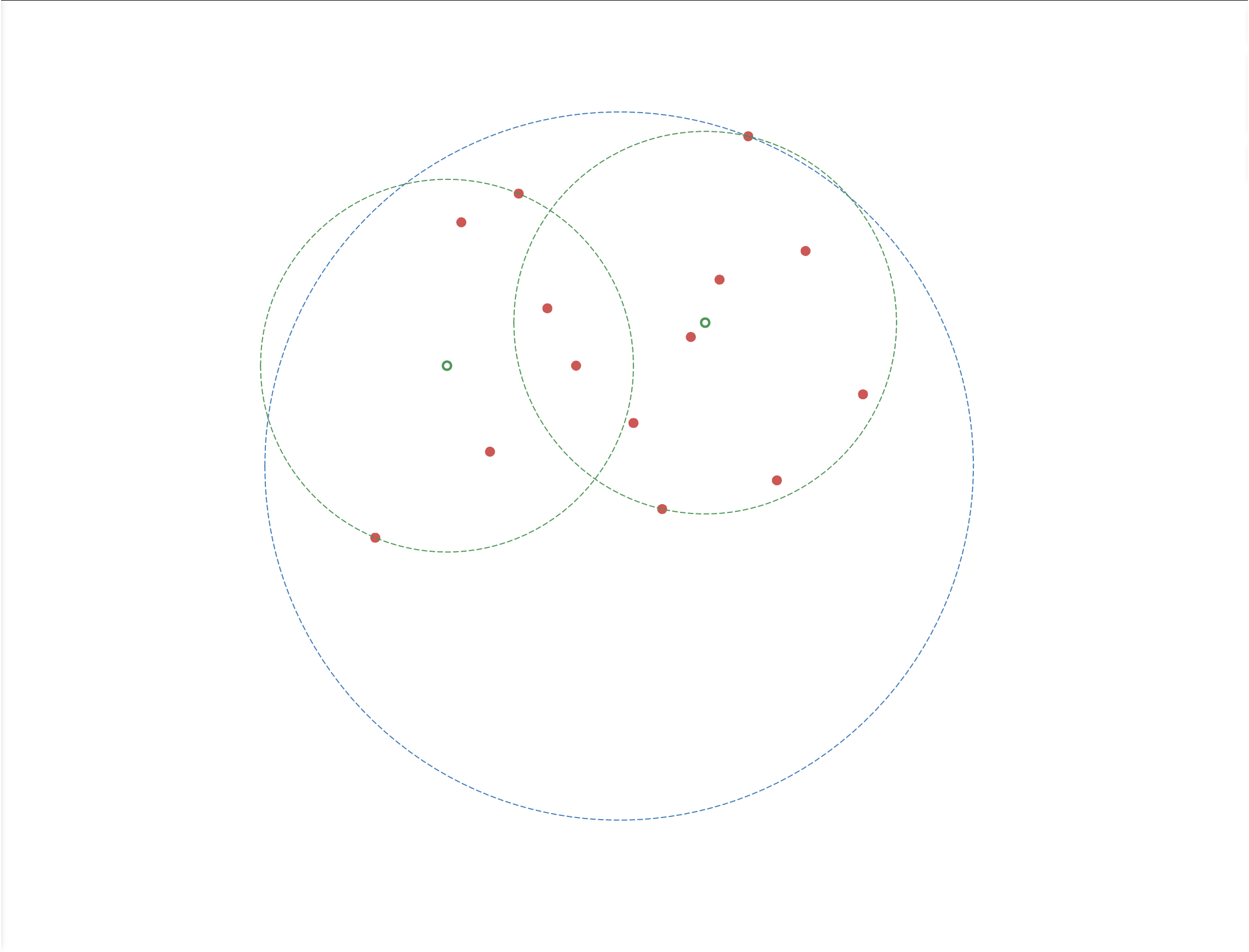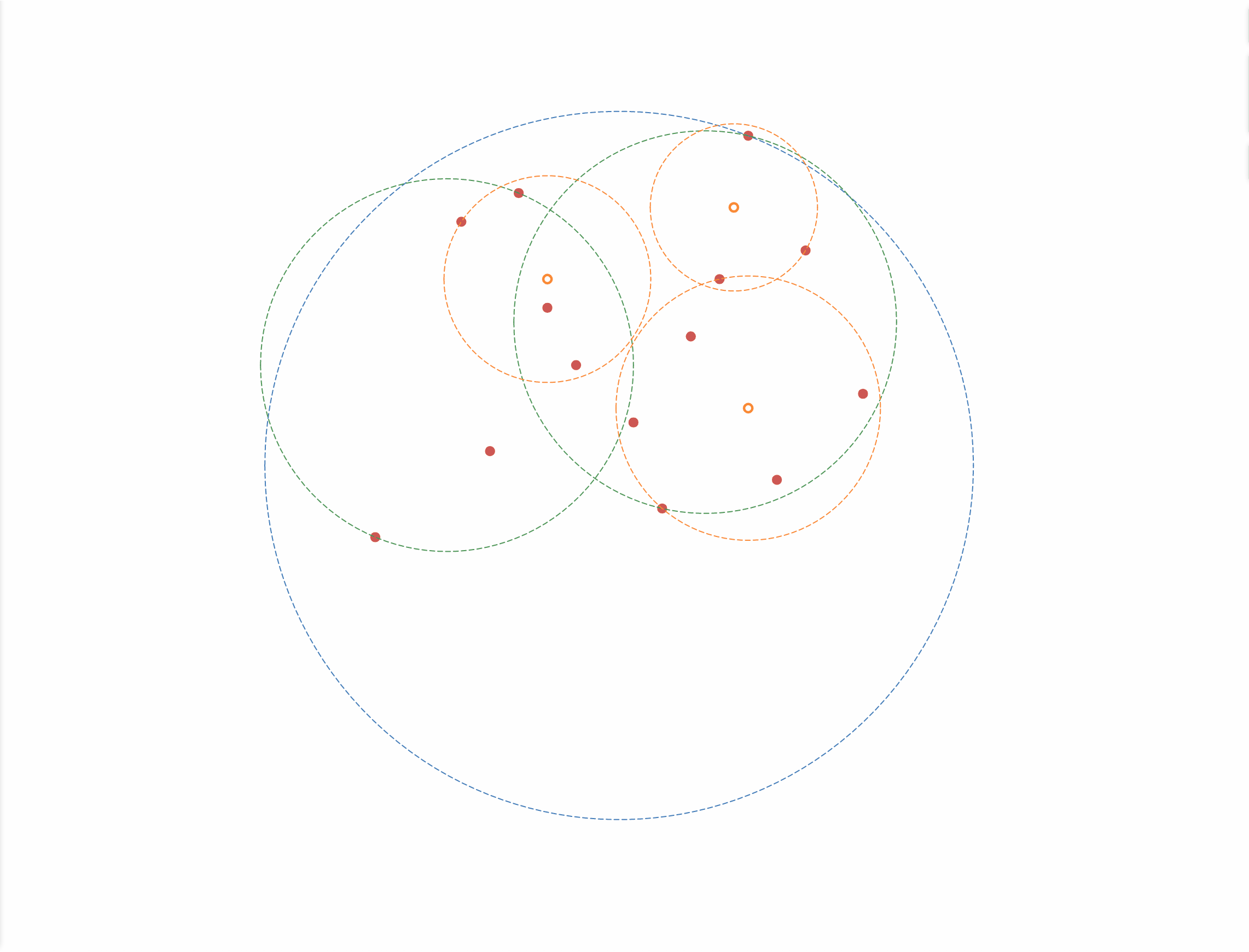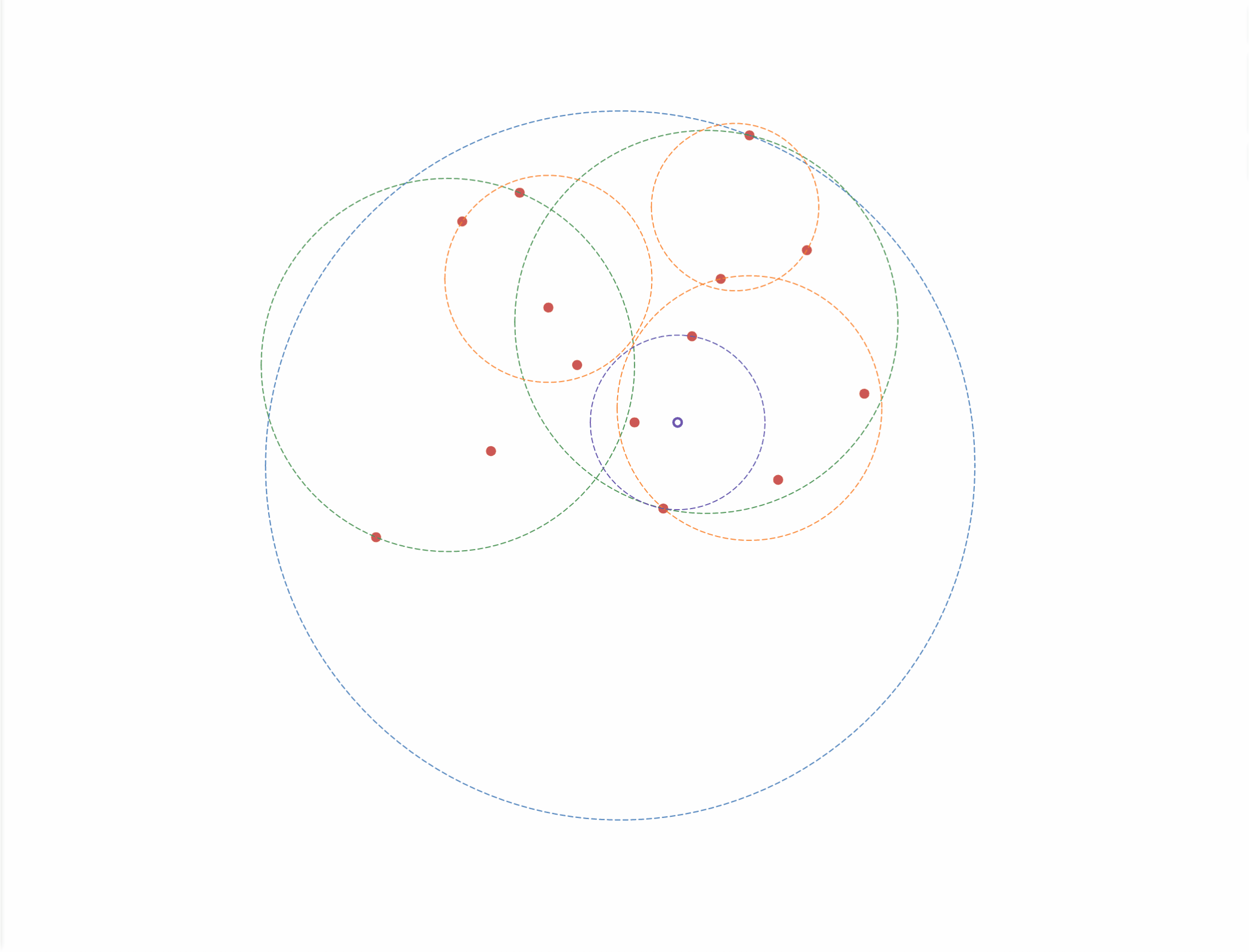
如图3-4 所示，根据一组二维的训练集，构建出一颗 Ball 树，步骤如下：

找到当前样本集中宽度最大的维度，并找到当前维度下最小与最大点的中点作为超球面的球心，即图中的蓝色空心点；
以球心到样本集中最远的距离作为半径，得到超球面，即图中的蓝色虚线；
按照样本点到球心的距离将当前样本集分成两个集合；
重复上述 1 - 3 步，直到无法切分停止算法；

查询 k 近邻

给定一个目标点，查询该点的 k 近邻。同 k-d 树一样，搜索包含该目标点的区域和以目标点为圆心，与当前最近点的距离作为半径的圆与超球面相交的区域，由于是球型与球型相交，相对于 k-d 树进一步减少了计算距离的次数。

图3-5

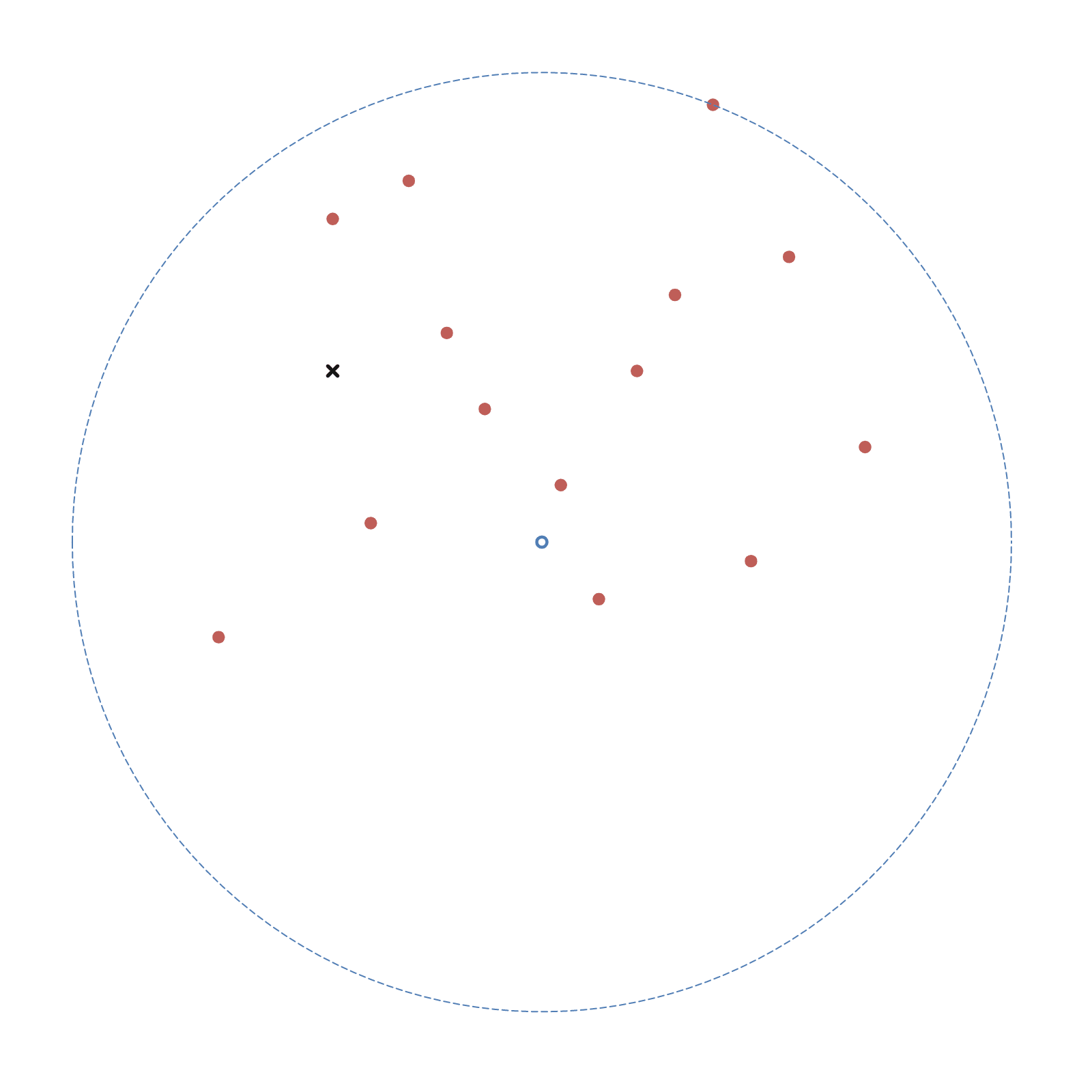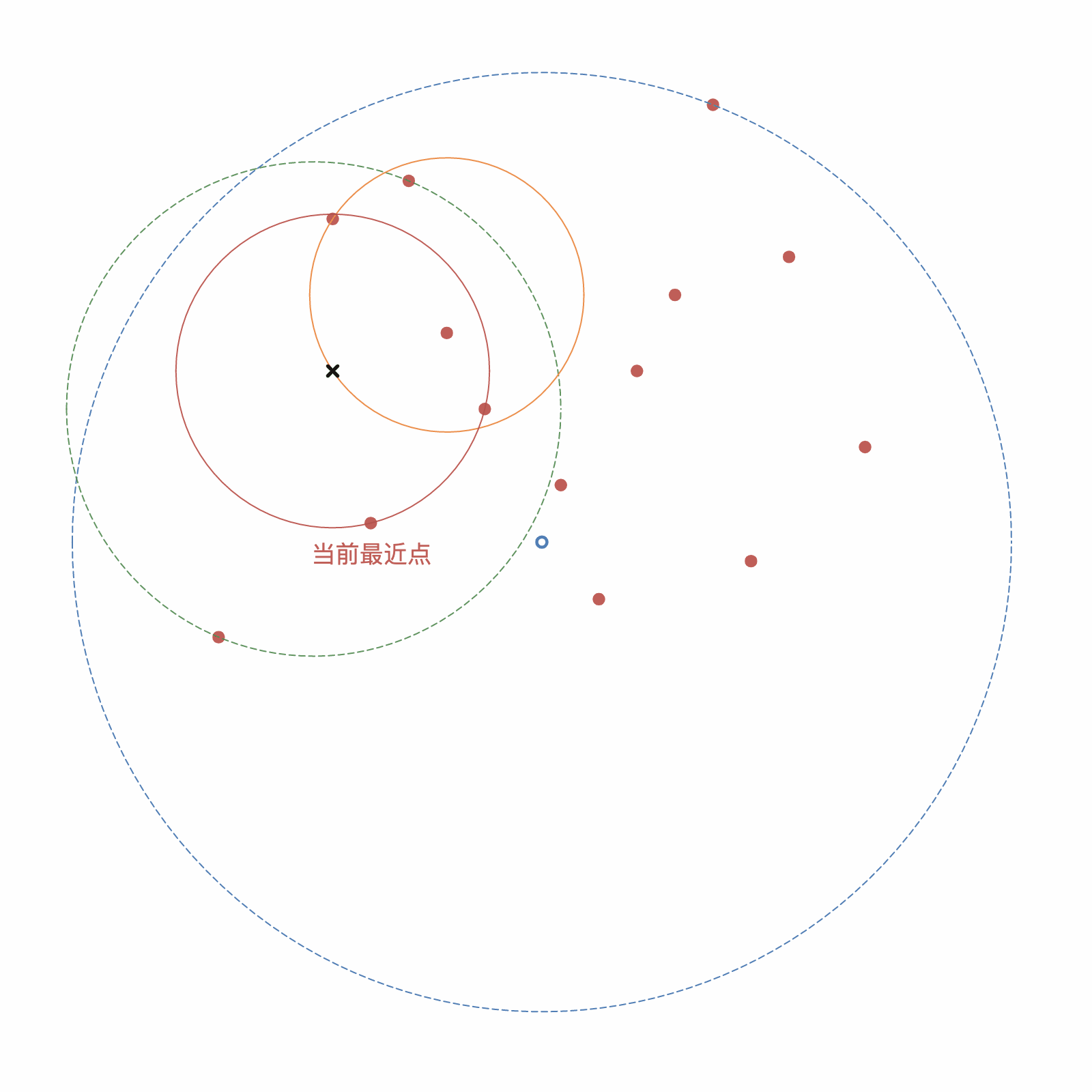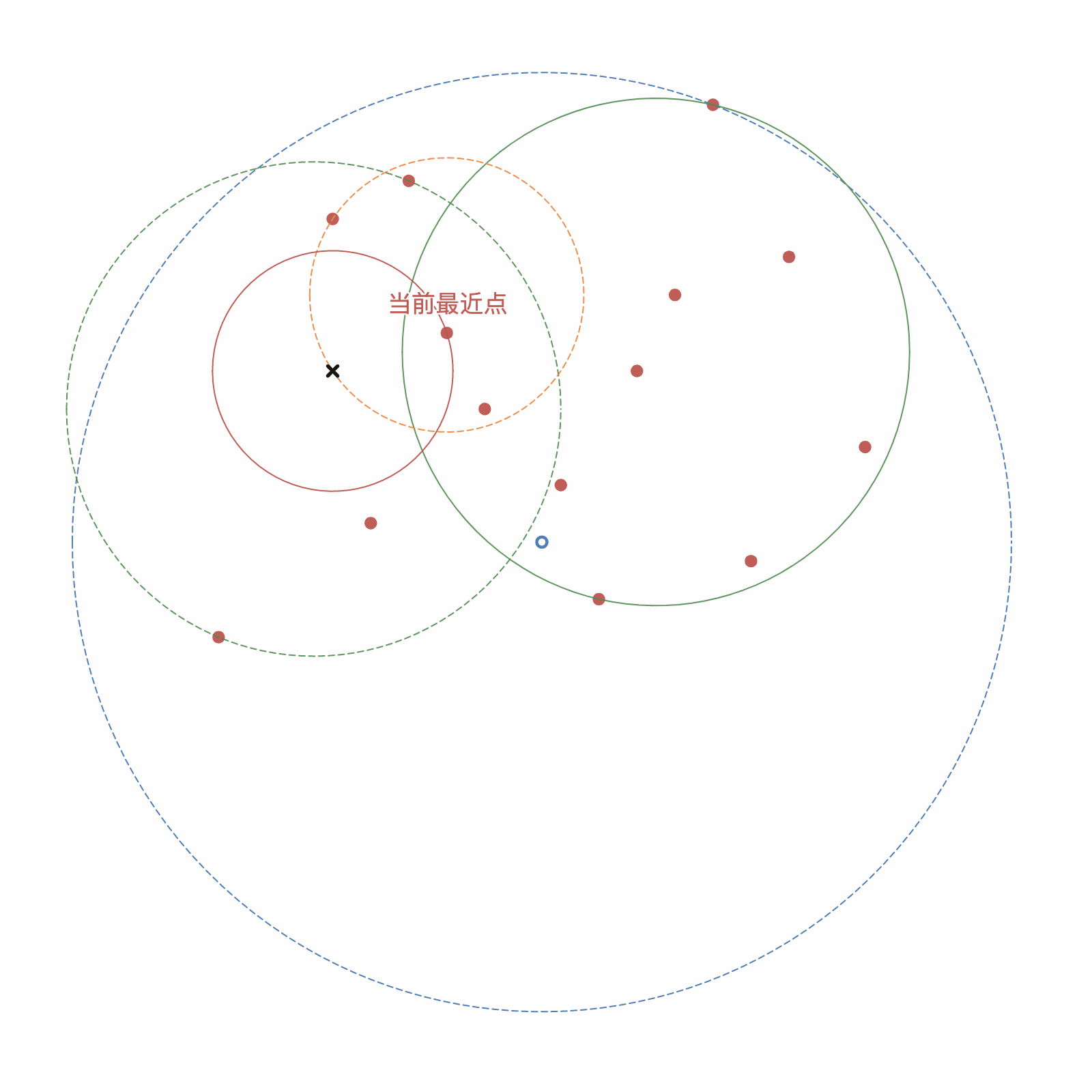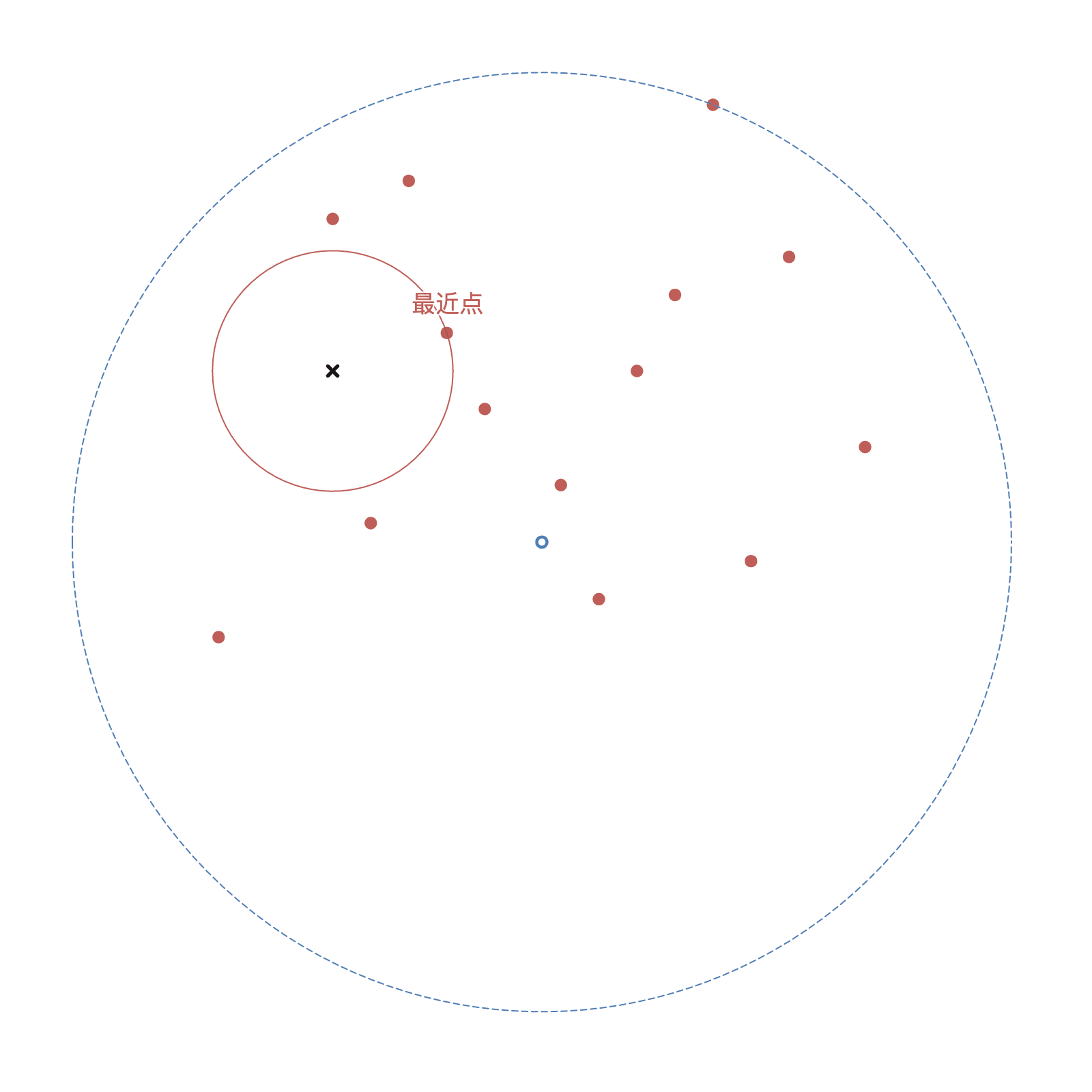
如图3-5 所示，给定一个目标点（图中黑色叉），根据构建出的 Ball 树，进行查询最近邻，步骤如下：

首先从根结点依次向下找到其中一个叶子结点，作为当前最近点，即图中左下的第二个点；
依次搜索每一个结点，当当前结点的形成的球与目标点形成的球相交时，说明可能存在比当前最近点更近的点，如图中第一个出现的橘色圆和第二个出现的绿色圆；
当两个球不相交时，则跳过该结点及其子结点，如图中第二、三个出现的橘色圆；
当全部结点都处理过后，结束搜索，当前最近点即为目标点的最近点；

与 k-d 树一样，当要搜索 k 个最近点时，只需要按顺序记录即可，算法步骤相同，具体实现可以参考下面的代码实现。

四、代码实现

使用 Python 实现 k-d 树

class kdnode:
    """
    k-d 树结点
    """
    
    def __init__(self, feature, value, index, left = None, right = None):
        # 结点对应特征的维度下标
        self.feature = feature
        # 结点对应训练集的特征值；当结点为叶子结点时，为特征向量
        self.value = value
        # 结点对应训练集的下标；当结点为叶子结点时，为下标向量
        self.inde