机器学习算法系列（二十二）-近似k近邻算法-Annoy（Approximate Nearest Neighbor / ANN）

阅读本文需要的背景知识点：k近邻算法、一丢丢编程知识

一、引言

  前面一节我们学习了机器学习算法系列（二十一）-k近邻算法（k-Nearest Neighbor / kNN Algorithm），其中介绍了两种查询最近的 k 个样本点的算法——k-维树（k-d tree）与Ball 树（Ball tree）。

  上面两种算法在样本不大、维度不多的情况下，可以精确快速地查询出最近邻，但是现实中往往都是百万级以上样本，数百维特征的数据集，上述的算法在某些应用场景下逐渐无法满足实时查询的要求，当该应用场景对搜索的精确性没有那么高的要求时，可以通过牺牲一些准确度来换取快速查询的性能，这就是所谓的近似 k 近邻算法¹ （Approximate Nearest Neighbor / ANN）。

  近似 k 近邻的算法有很多，下面分三篇文章分别介绍三个有代表性的算法，这一节先来看看一种基于树的算法——Annoy²（Approximate Nearest Neighbors Oh Yeah）。

二、模型介绍

  Annoy 算法是由 Erik Bernhardsson 在 Hack Week 期间用几个下午构建出来的，被应用于著名音乐应用 Spotify 的音乐推荐中，其结构与上一节中提到的 k-维树（k-d tree）与 Ball 树（Ball tree）一样，也是一种基于二叉树结构的算法。

Annoy 二叉树构建

  构建一棵二叉树的步骤如图 2-1 ：

图 2-1

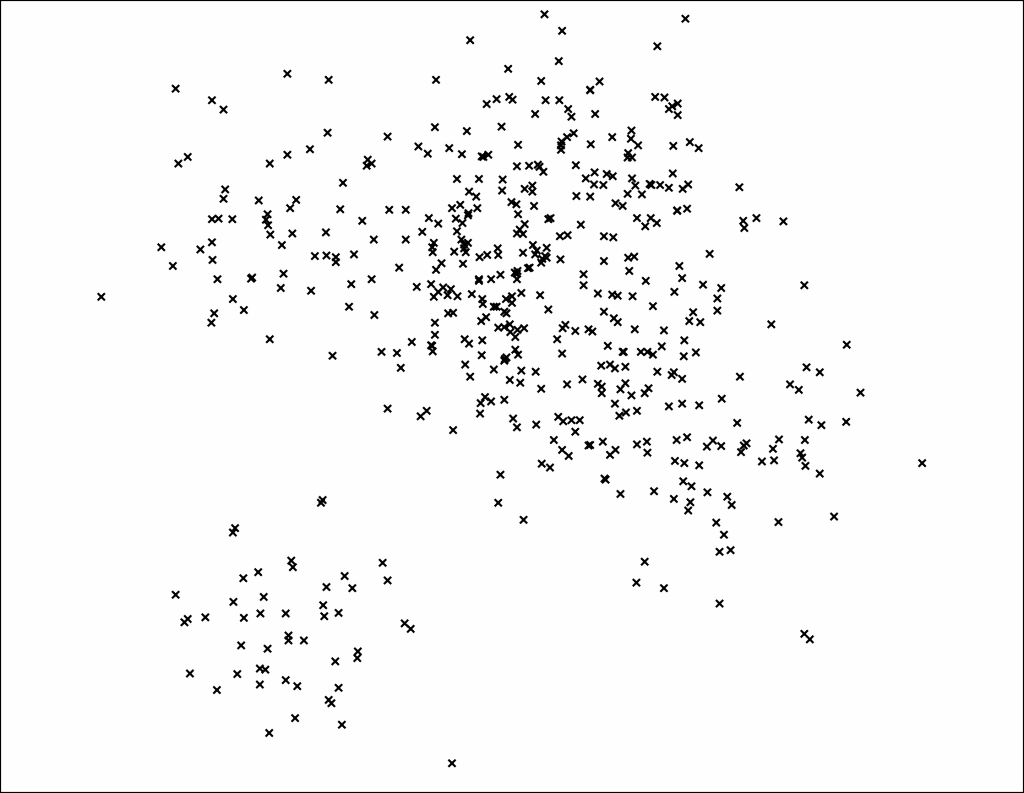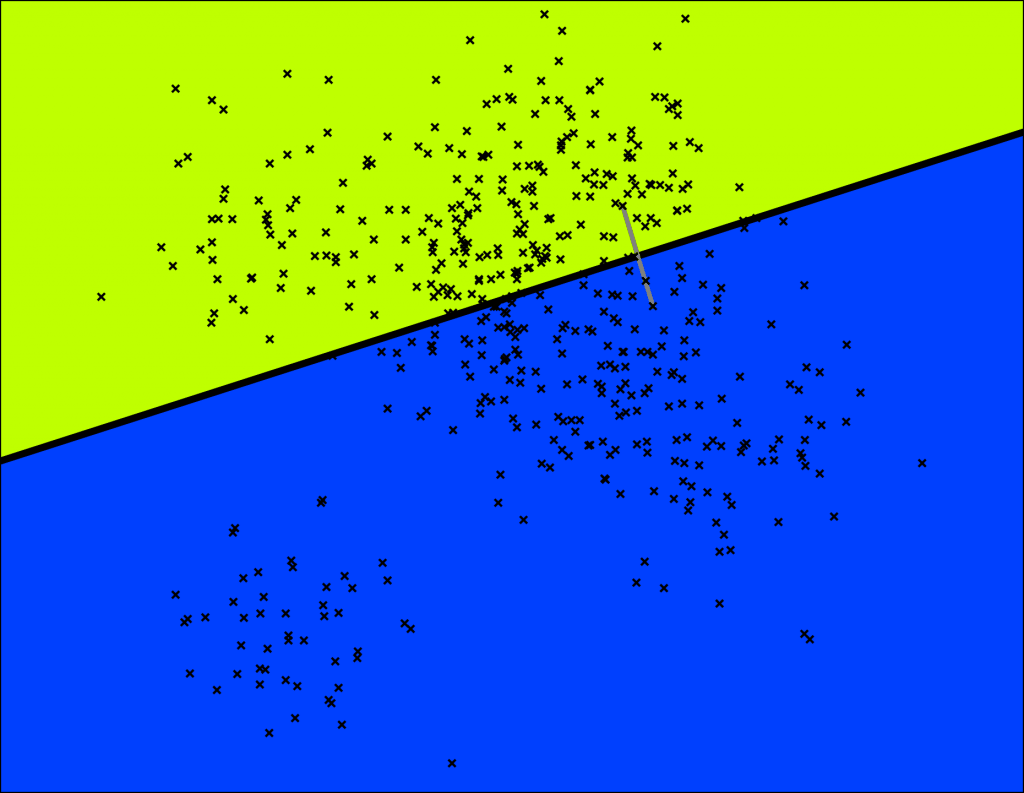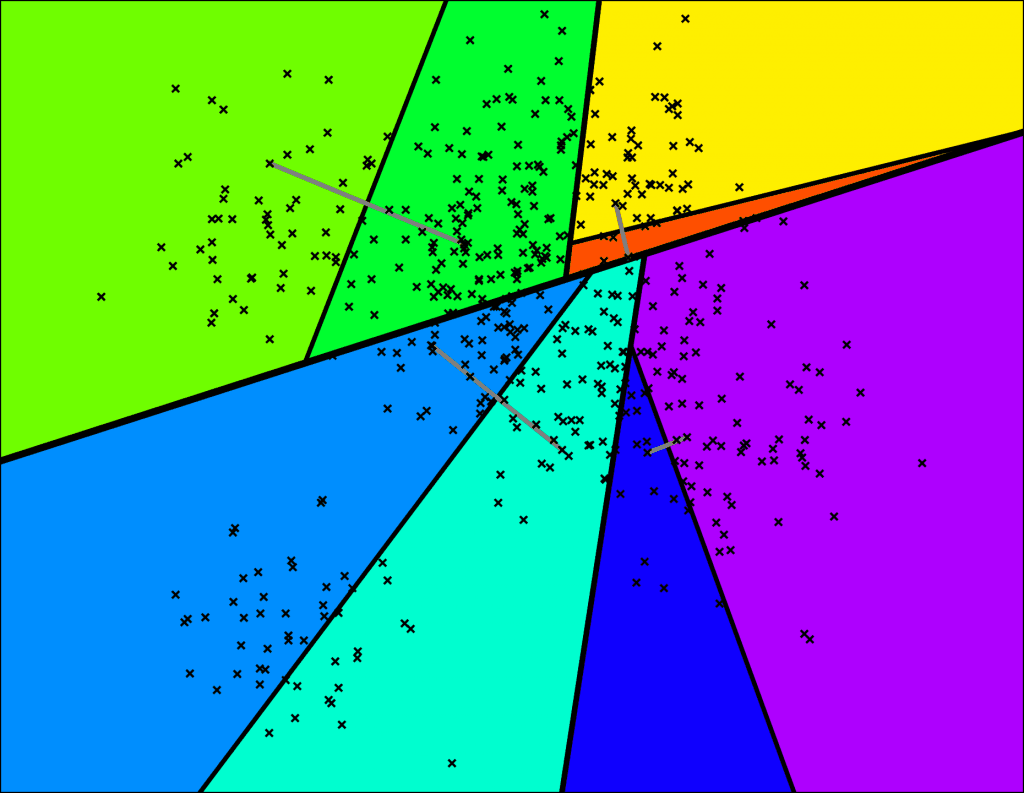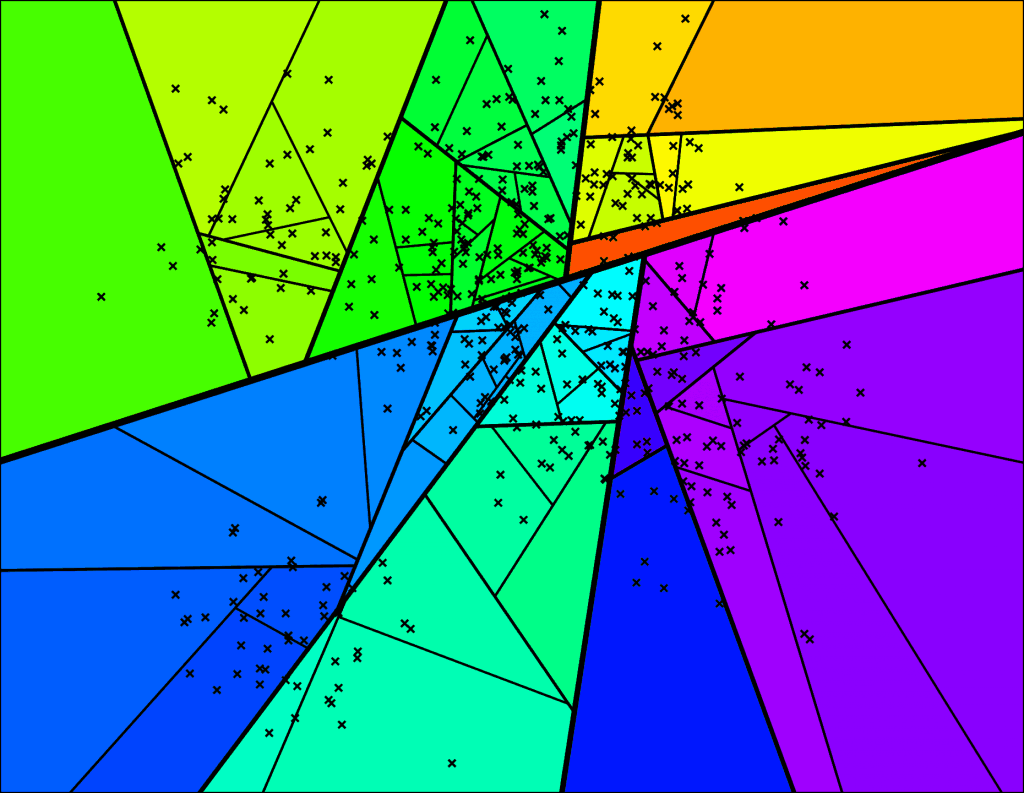
  首先随机选取两个样本点，构建一个与这两个样本点 P、Q 等距的超平面（图中的粗黑线）作为分割平面，然后依次递归地进行分割，直到样本点无法被分割或剩余样本点小于等于指定的数量为止。
  结点超平面的法向量为：
$$w=P-Q$$

式 2-1

  结点超平面的偏移量为 ：
$$b=-\frac{P+Q}{2}w$$

式 2-2

  最后得到一棵二叉树如图 2-2 所示：

图 2-2

查询 k 近邻

  查询 k 近邻时只需顺着二叉树由上至下找到对应的叶子结点即可。但是上面的查询方式会产生几个问题：

1. 当最近点刚好在划分超平面的外面怎么办？
2. 当要查询的近邻数量大于叶子结点中包含的样本数量怎么办？

  针对上面两个问题，其中一种优化的技巧是使用优先级队列，不再只查下一个叶子结点，而是按照距离的优先级，多查询几个叶子结点。另一种优化技巧是构造一片由多棵二叉树组成的森林，查询时同时搜索所有的二叉树。组合上面两种优化方法后的搜索过程如图 2-3 所示：

图 2-3

  最后的搜索范围组合后如图 2-4 所示，最后在搜索范围内查询 k 近邻。

图 2-4

Annoy 二叉树平衡

  在构造单棵二叉树运气不好时，每次随机选取的两点都靠近数据集的边缘，构造出的树极度不平衡，导致树的深度过深，会影响搜索时的效率，annoy 算法不是简单的随机选取两个点，而是通过一种启发式的方法来平衡二叉树两边的子树，步骤如下图 2-5 所示：

图 2-5

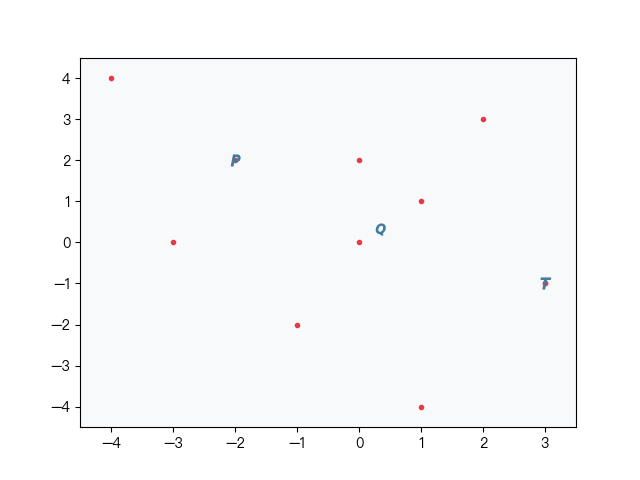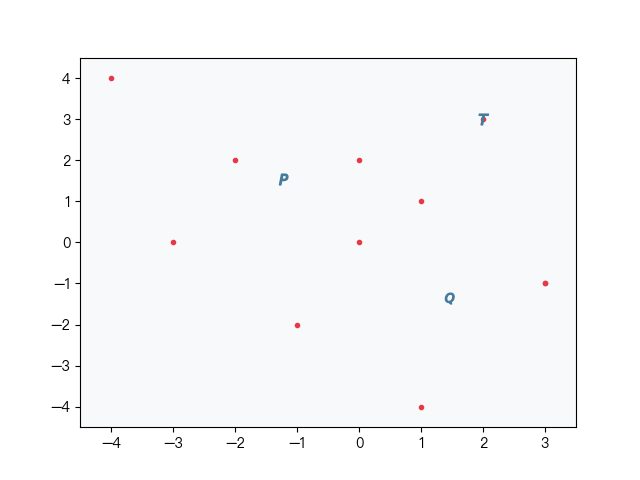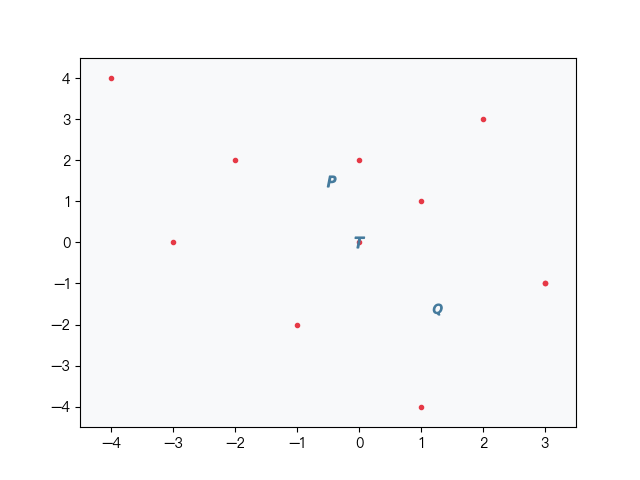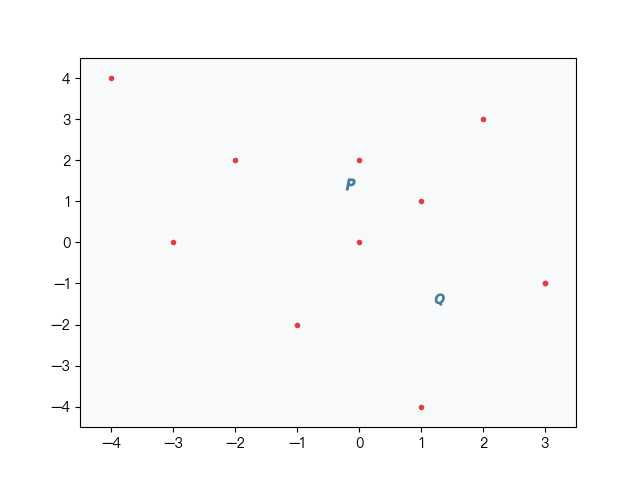
  首先在样本集中随机选取两个点（如图中的点 P、Q），再在样本集中随机选择一个目标点 T，计算点 P、Q 与点 T 的距离，取距离近的点向目标点移动，移动的距离取决于循环的次数。重复以上操作，最后得到平衡后的 P、Q 两点，具体的算法可参考下面的代码实现或 Annoy 的源码。
  更多详细的算法演示请参考 Annoy 作者的博客文章介绍³，上面的大部分图片同样出自该文章。

三、算法步骤

Annoy 构建

1. 启发式的选取两个样本点
2. 计算并记录与两个样本点等距的超平面，作为一个结点
3. 根据样本点在超平面的位置决定被分配到哪一边的子树中
4. 当样本点无法被分割或剩余样本点小于等于指定的数量时，结束算法
5. 重复上述步骤，构建多棵二叉树

查询 k 近邻

1. 将所有二叉树的根结点插入到优先级队列中
2. 按优先级搜索队列中所有的结点，直到搜索到了指定次数的结点
3. 去除重复的样本点
4. 计算距离排序后返回最近的 k 近邻

四、原理证明

超平面的偏移量

（1）超平面的表达式
（2）由定义可知 P、Q 的中点一定在超平面上
（3）移项后就得到了超平面的偏移量
$$\begin{array}{rl}& wx+b=0\\ & \\ & \end{array}$$