k最近邻算法

原创已于 2022-08-29 17:32:45 修改 · 1.4k 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#近邻算法 #机器学习 #数据挖掘

于 2022-07-20 16:24:02 首次发布

算法专栏收录该内容

12 篇文章

订阅专栏

k最近邻算法

K最近邻概述

所谓K最近邻，就是k个最近的邻居的意思，每个样本都可以用它最接近的k个邻居来代表
K最近邻算法的核心思想是：如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性.
- 一种基本分类与回归方法
- 要求必须有y,y是离散类型的
K最近邻分类算法是数据挖掘分类技术中的方法之一
采用测量不同特征值之间距离的方法进行分类.简单来说：就是近朱者赤，近墨者黑。
KNN是一种没有显示的过程,在训练阶段把数据保存下来,等受到测试样本后进行处理

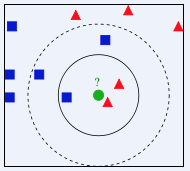
三角形为女生,正方形为男生,有一个未知的圆点,谁靠它最近,或者在一定范围内,哪个类别靠近它的数量多,它就属于哪个类

K最近邻算法原理

已知条件: 训练数据集已经是分类完成的

设定k的值
计算出测试集样本点与各个训练集样本点之间的距离：（常用：欧式距离、曼哈顿距离）
选择离测试集样本点最近的k个训练集样本点
计算前k个点所属类别的出现频率
返回频率最高的的类别作为测试集样本点的类别

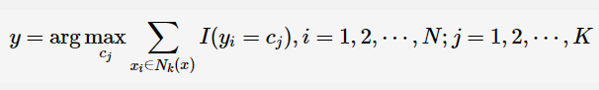
K最近邻计算原理-距离度量

欧式距离

曼哈顿距离

夹角余弦

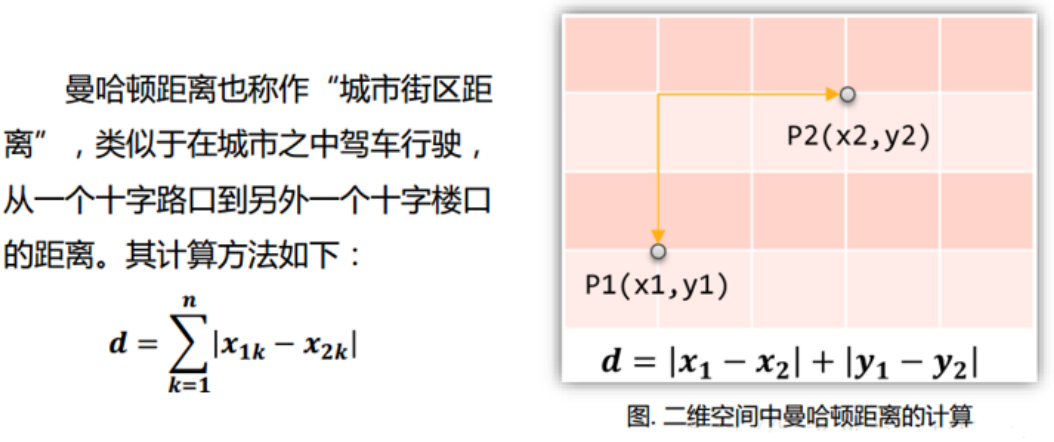
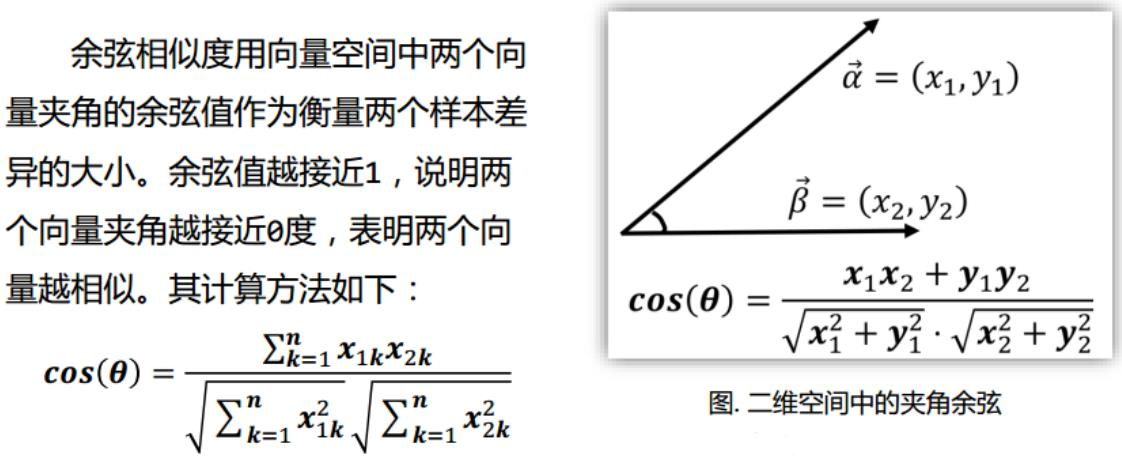
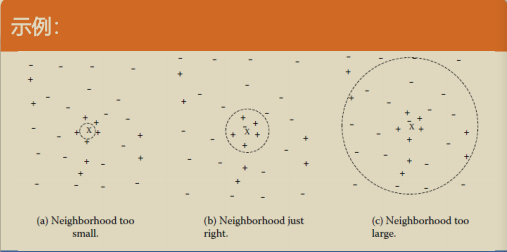
K值

k太小,分类容易受噪声点影响;k太多,近邻中又可能包含太多其他类的点,所以,k非常重要
经验：K一般低于训练样本数的平方根,但训练样本少的时候,k可以适当高于训练样本数的平方根

类别判定

投票决定：少数服从多数，近邻中哪个类别的点最多就分为该类
加权投票法：根据距离的远近，对近邻的投票进行加权，距离越近则权重越大（权重为距离平方的倒数）

K最近邻计算原理

**局部学习方法：**K-NN算法的核心思想非常简单：在训练集中选取离输入的数据点最近的k个邻居，根据这个k个邻居中出现次数最多的类别（最大表决规则），作为该数据点的类别

K最近邻-修正

经典k邻域的样本点对预测结果的贡献度是相等的。而一个简单的思想是距离更近的样本点应有更大的相似度，其贡献度应比距离更远的样本点大

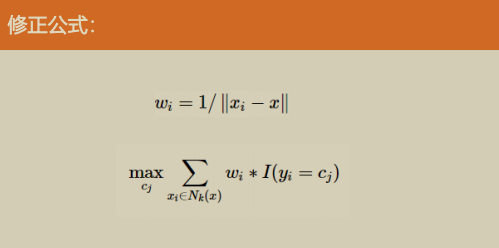
K最近邻算法特点

训练时间为零，只是把样本保存起来，没有显示训练过程，是一种典型的懒惰学习(lazy learning)，基于实例的学习
特别适合多分类问题(multi-model,对象具有多个类别标签)，KNN比SVM的表现要好
和朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感
计算量巨大，时间复杂度高，空间复杂度高
样本不平衡时，对稀有类别的预测准确率低
非常依赖训练数据的准确性

K最近邻算法总结

一种非参数、惰性学习方法，导致预测时速度慢
当训练样本集较大时,会导致其计算开销高
样本不平衡的时候，对稀有类别的预测准确率低
KNN模型的可解释性不强

K最近邻优缺点

优点:

KNN是一种在线技术，新数据可以直接加入数据集而不必进行重新训练
KNN理论简单，容易实现
精度高、对异常值不敏感、无数据输入假定

缺点:

对于样本容量大的数据集计算量比较大
样本不平衡时，预测偏差比较大，如：某一类的样本比较少，而其它类样本比较多
KNN每一次分类都会重新进行一次全局运算
计算复杂度高、空间复杂度高
k值大小的选择
适用数据范围：数值型

K最近邻代码实现

导入模块

from sklearn.neighbors import KNeighborsClassifier

K最近邻代码实现-模型方法★

方法名	含义
fit(X, y)	使用X作为训练数据,y作为目标值(类似于标签）来拟合模型。
get_params([deep])	获取估值器的参数。
kneighbors([X, n_neighbors,return_distance])	查找—个或几个点的K个邻居。
kneighbors_graph([X,n_neighbors, mode])	计算在X数组中每个点的k邻居的(权重)图。
predict(X)	给提供的数据预测对应的标签。
predict_proba(X)	返回测试数据X的概率估值。
score(×, y[. sample_weight])	返回给定测试数据和标签的平均准确值。
set_params(**params)	设置估值器的参数。

K最近邻代码实现-模型参数

n_neighbors: int,可选参数(默认为5)用于kneighbors查询的默认邻居的数量
weights(权重):str or callable(自定义类型),可选参数(默认为‘uniform')
- 用于预测的权重函数。可选参数如下:
  - 'uniform':统一的权重.在每一个邻居区域里的点的权重都是一样的。
  - 'distance':权重点等于他们距离的倒数。使用此函数，更近的邻居对于所预测的点的影响更大。
  - callable : 一个用户自定义的方法，此方法接收一个距离的数组，然后返回一个相同形状并且包含权重的数组。
algorithm(算法):{'auto' , 'ball_tree', 'kd_tree', 'brute'},可选参数(默认为'auto')
- 计算最近邻居用的算法:
  - bal_tree是为了克服kd树高纬失效而发明的，其构造过程是以质心C和半径r分割样本空间，每个节点是一个超球体。
  - 'kd_tree'构造kd树存储数据以便对其进行快速检索的树形数据结构，kd树也就是数据结构中的二叉树。以中值切分构造的树，每个结点是一个超矩形，在维数小于20时效率高。
  - 'brute'使用暴力搜索.也就是线性扫描，当训练集很大时，计算非常耗时
  - 'auto'会基于传入fit方法的内容，选择最合适的算法。
metric(矩阵): string or callable,默认为‘minkowski'
- 用于树的距离矩阵。默认为闵可夫斯基空间，如果和p=2一块使用相当于使用标准欧几里得矩阵.所有可用的矩阵列表请查询DistanceMetric的文档。
metric_params(矩阵参数): dict,可选参数(默认为None)
- 给矩阵方法使用的其他的关键词参数。
n_jobs: int,可选参数(默认为1)
认为闵可夫斯基空间，如果和p=2一块使用相当于使用标准欧几里得矩阵.所有可用的矩阵列表请查询DistanceMetric的文档。
metric_params(矩阵参数): dict,可选参数(默认为None)
- 给矩阵方法使用的其他的关键词参数。
n_jobs: int,可选参数(默认为1)
- 用于搜索邻居的，可并行运行的任务数量。如果为-1,任务数量设置为CPU核的数量。不会影响fit方法。