由注意力机制中scaled sqrt(dk)操作联想到期望与方差的本质推导

在注意力机制文章Attention Is All You Need中，作者在计算dot-product attention时，引入了一个scaled因子，即

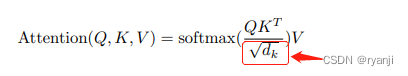
之所以引入scaled因子，是让数据符合0均值、方差1的分布。因为qk^T内积操作后，数据期望为0、方差为d_k，那么softmax梯度会消失。
接下来就开始解释原因。

引入期望、方差的定义

1、期望

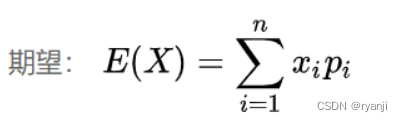
期望计算的是样本的均值，描述一个随机变量的集中位置或者平均位置。

2、方差

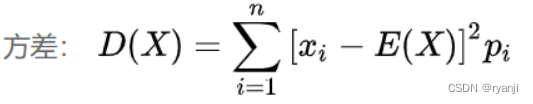
方差计算的是随机变量与期望的偏离程度，描述的是预测值与真实值之间的波动情况。方差越大，数据波动越大，越不均匀。(埋伏笔，这会对softmax有影响)

3、公式

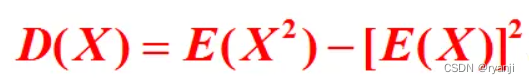
自己写了一个推导过程，如下：
记住：期望就是在x上套了个壳，没那么复杂，就是乘以概率p

官方证明如下，当你理解了套壳之后，官方证明也容易看懂了

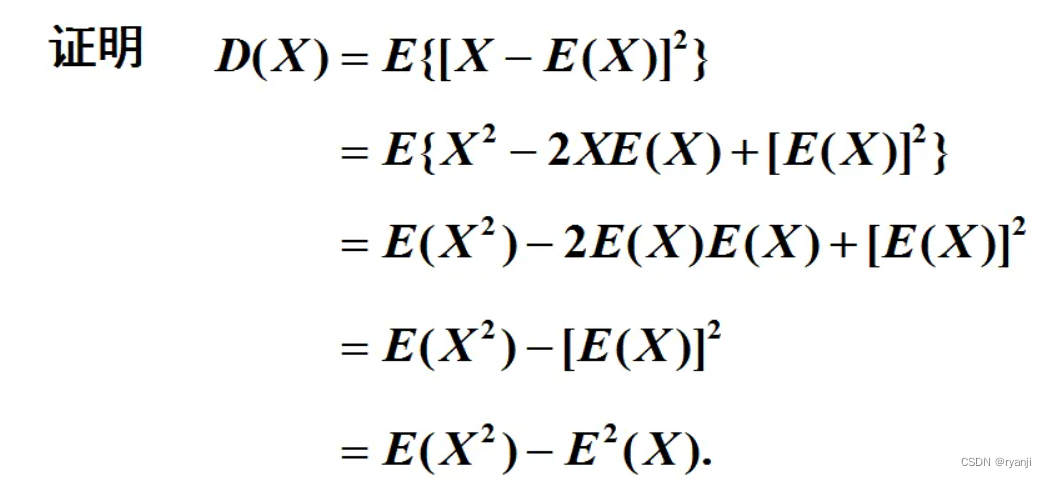
那既然会套壳，接下来这个你是不是也能证明了

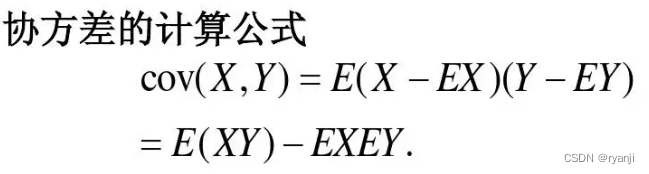
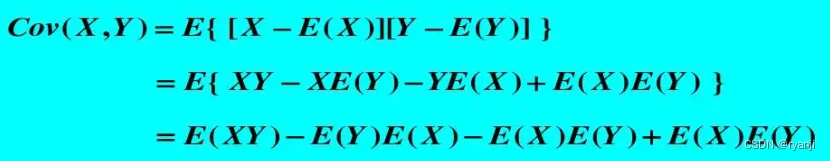
4、那么QK^T 的方差和期望怎么计算呢？

我们知道，Q和K都是由同一个隐藏层上通过不同的权重矩阵得到的，所以Q和K里的每一个向量都是相互独立。假设Q,K是5×200的大小矩阵，即包含200维的5个向量q_i ,k_i。i是从1到5。
参考我们上面3小节推导的公式。
因为Q,K是独立分布的，那么E[q_i]=E[k_i]=0
又因为协方差为0，所以E[q_ik_i]=E[q_i]E[k_i]=0

因此，QK^T的期望是

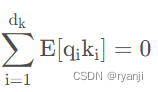
因为Q,K是独立分布的，那么D[q_i]=D[k_i]=1
D[q_i]=E(q_i²)-(E[q_i])²=E(q_i²)=1,同理E(k_i²)=1
D[q_ik_i]=E[(q_ik_i)²]-(E(q_ik_i))²=E[(q_ik_i)²]=E[(q_i)²(k_i)²]=E(q_i²)E(k_i²)=1

因此，QK^T的方差是

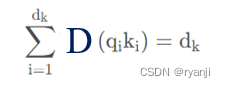
5、scaled的好处

既然QK^T的方差不为1，那么我们就除以d_k的开方。为什么是开方呢？因为方差计算公式中有个平方操作，表达式除以d_k开方，方差就是除以d_k。所以scaled操作得到的数据分布是期望为0，方差为1。
`那为什么方差d_k时候，softmax不好呢？
softmax的公式如下（参考链接：https://zhuanlan.zhihu.com/p/279142777）

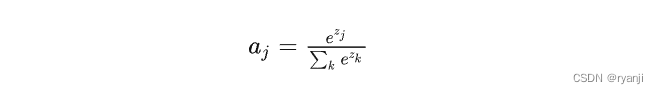
梯度为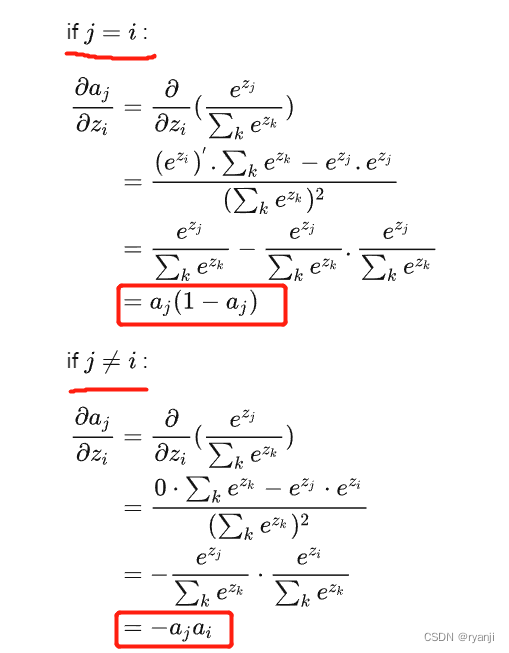
所以，当随着d_k变大时，方差波动越大，假如q1比其他值都大很多，那么softmax的值趋近于0.无论是j=i,或者j不等于i。softmax是一个概率输出，输出每一个类别的概率值。当某一个值比重很大，那么它输出概率很高，接近于1，反向梯度越接近于0。梯度为0，则反向传播无法更新权重参数，模型训练受影响。