附录A 特征方程和通项公式

当n>2时:F(n)即 ,它的特征方程为:
,它的特征方程为:

求解得:
 ,
,
那么F(n)的通项公式为:
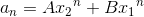
斐波那契数列中
 本文介绍了特征方程和通项公式在解决数列问题中的应用,特别是针对斐波那契数列。通过解特征方程找到通项公式,揭示了指数级增长的算法效率问题。对于线性数列,通过建立特征方程求解通项,展示了如何利用等比数列公式得出最终的通项表达式。
本文介绍了特征方程和通项公式在解决数列问题中的应用,特别是针对斐波那契数列。通过解特征方程找到通项公式,揭示了指数级增长的算法效率问题。对于线性数列,通过建立特征方程求解通项,展示了如何利用等比数列公式得出最终的通项表达式。

当n>2时:F(n)即 ,它的特征方程为:
,它的特征方程为:

求解得:
 ,
,
那么F(n)的通项公式为:
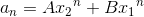
斐波那契数列中
 4017
4017
 631
631

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


