积分直方图的实现(Integral Histogram)

原创

于 2021-01-11 17:54:10 发布 · 1.1k 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #动态规划

本文介绍积分直方图的概念及其计算方法。积分直方图是基于图像的积分图，用于统计图像区域内各灰度级像素的出现次数。文章提供了一个计算积分直方图的函数，并给出了测试用例，要求在保持计算复杂度合理的情况下处理灰度图像的积分直方图计算。

题目描述

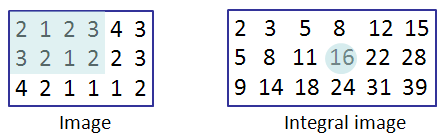
如图所示，左侧为一幅灰度图像I，其积分图如右图所示，积分图与左侧图像等大（宽=6，高=3），积分图中第（i,j）个元素的元素值Integral(i, j)，等于原图像I中第（i,j）个像素左上角所有像素的像素值之和，如图中积分图中Integral(2,4) = 16 = 2+1+2+3+3+2+1+2 = I(1,1) + I(1,2) + I(1,3) + I(1,4) + I(2,1) + I(2,2) + I(2,3) + I(2,4)；

类似地，一幅图像I的积分直方图H的定义如下：一幅图像的积分直方图与该图像等大（宽、高相等），积分图中第(i,j)个元素的元素值为该图像第(i,j)个像素左上角所有像素像素值统计获得的直方图，如下图所示。

左侧灰度图像中，像素值范围0-9，共10个灰度阶，其积分直方图第(4,5)个元素的元素值H(4,5)为一个直方图，其中左侧图像中第(4,5)个像素左上角区域中，像素值为0-9的像素个数分别是2,1,4,3,2,2,2,1,2,1，因此，如果积分直方图中每个直方图共有10个bin，那么，H（4,5）= [2,1,4,3,2,2,2,1,2,1]。

问题：