PSO优化RBF三维曲面重建

第三章 使用经粒子群优化调整的径向基函数进行三维曲面重建

3.1. 引言

本章介绍了使用粒子群优化（PSO）训练的径向基函数神经网络（RBF），以解决从三维测距扫描仪获取的点云中重建表面的问题。

为了插值得到紧凑表面表示的点云网格化函数在计算机辅助设计（CAD）、机器人建图以及物体描述与识别等重要应用中非常关键。然而，不同应用对插值的精度和质量的衡量标准各不相同。在计算机辅助设计（CAD）中，获得光滑曲面并确保其为流形至关重要；而在机器人建图和物体描述与识别中，则必须获取紧凑（低存储、低维度）且信息丰富或具有足够代表性的对象或环境表示。也就是说，所获得的表面应能描述对象或环境的形状，而无需包含过多细节（或无需保证流形条件）。本文提出一种利用粒子群优化训练径向基函数的方法，以满足所有应用对精度和质量的要求。也就是说，我们的方法可配置用于获取紧凑表示、非高度细节化的表面，适用于机器人建图或物体识别，也可配置用于生成光滑的融合曲面并确保其为流形。此前已有研究使用径向基函数进行表面重建 from 点云[1]由于它们具有紧凑的功能描述，并且插值和外推在其函数表示中是固有的。然而，这些方法一直使用梯度下降方法进行训练，而梯度下降方法极易陷入局部极小值，并且不易并行化。我们提出了一种基于粒子群优化的径向基函数训练方法，从而获得一个精确且快速的点云插值系统，这得益于其并行化特性。利用径向基函数获取表面的优势此前已被萨夫琴科[4],特克和奥布莱恩[6],以及卡尔[2]等人报道过。然而，这些工作并未针对诸如激光雷达传感器获取的大规模数据集进行处理。文献中提出的系统对此问题具有显著优势，但其采用的是传统的径向基函数训练方法，计算成本高且收敛速度慢。

接下来，我们提出了解决此问题的方案，主要基于使用粒子群优化算法作为径向基函数的训练方法，以获得一种并行化算法，该算法收敛速度更快，同时具有足够的精度，能够生成稠密点云的平滑且具代表性的表面。

3.2. 径向基函数

这类神经网络具有三层结构：输入层、一个隐藏层和输出层，如图3.1所示。

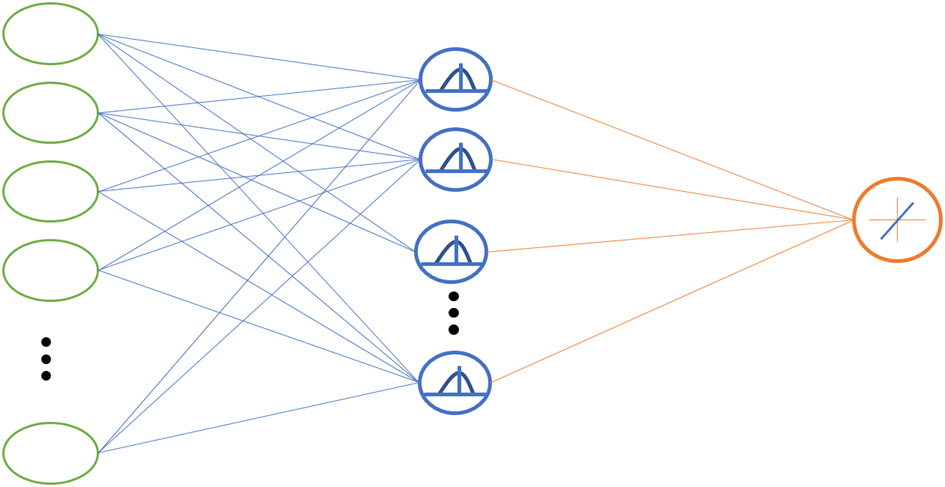
尽管该网络的结构可能与多层感知器（MLP）的结构相似，但主要区别在于隐藏层神经元会计算权值向量（在径向基函数网络中称为中心或质心）与输入向量之间的欧几里得距离。该计算出的距离作为具有高斯形状的径向基函数的评估参数。

有多种方法可以训练径向基函数的隐藏层；最常用且广为人知的是名为K‐means的算法。本章中我们采用的就是该算法。

K‐means是一种使用无监督学习类型的聚类算法，其中K是我们希望找到的簇的数量，也就是隐藏层的神经元数量。后者是一个用户参数，需要预先设定。算法K‐means的步骤如下：
1. 初始化权值向量（每个簇的中心或质心）。通常通过将训练数据集的前k个样本的值赋给权值向量来完成初始化：c1 = x1, c2 = x2, …, ck = xk，其中cj是第j个中心（或权值向量），xi是第i个样本训练数据集，其中 j = 1,…, k 和 i = 1,…,N；N 是训练样本的总数。
2. 在每次迭代过程中，将数据样本分配给一个簇：对于样本数据 xi，计算 xi 与各个簇中心 cj 之间的距离。将样本 xi 分配给距离中心更近的簇。
3. 为每个簇计算新的中心向量cj。它们被计算为属于每个簇的样本向量的均值向量。上述过程等同于计算每个模式分布的质心，假设簇中所有模式具有相同的权重。
4. 如果中心的值相对于前一次迭代发生了变化，则返回步骤2。否则，已达到收敛，训练过程结束。

The K‐means 算法确保了凸性，同时也将输入的数据集划分为一个分区，称为沃罗诺伊划分，如图3.2所示。

确定中心后，需要计算每个高斯函数的标准差。每个神经元的标准差按公式 (3.1)对簇中的所有 x进行计算。

$$
σ = \sqrt{E[(X − ck)^2]} \tag{3.1}
$$

此处，E表示平均值或期望值，ck是每个簇的均值向量值。

然后，每个高斯函数的中心和扩展被固定，如图3.3所示。

最后，调整输出权重以插值函数y: n → 。由于网络的输出是输入向量的标量函数，该网络输出由方程给出

$$
F(x) = \sum_{i=1}^{N} w_i \phi(|x - c_i|), \tag{3.2}
$$

其中 $\phi(|x - ci|) = \exp\left(-\frac{|x - ci|^2}{2\sigma^2}\right)$，且范数通常为欧几里得距离或马氏距离。

因此，可以通过求解以下方程得到权重值：

$$
\begin{bmatrix}
\phi_1(x_1) & \phi_2(x_1) & \phi_3(x_1) & \dots & \phi_N(x_1) \
\phi_1(x_2) & \phi_2(x_2) & \phi_3(x_2) & \dots & \phi_N(x_2) \
\vdots & \vdots & \vdots & \ddots & \vdots \
\phi_1(x_N) & \phi_2(x_N) & \phi_3(x_N) & \dots & \phi_N(x_N)
\end{bmatrix}
\begin{bmatrix}
w_1 \ w_2 \ \vdots \ w_N
\end{bmatrix}
=
\begin{bmatrix}
y_1 \ y_2 \ \vdots \ y_N
\end{bmatrix}, \tag{3.3}
$$

其中插值矩阵的元素为 $[\phi_{iq}]$，i, q = 1,…,N。定义向量 $w=[w_i]$ 和 $y=[y_i]$，式(3.3)可写为

$$
\Phi w = y. \tag{3.4}
$$

根据米切利（1986）的定理，如果点 $x_i$互不相同，则插值矩阵 $\Phi$是非奇异的，且权重 $w$可通过简单的线性代数求解：

$$
w = \Phi^{-1} y. \tag{3.5}
$$

3.3. 使用径向基函数和粒子群优化进行曲面插值

本节提出使用粒子群优化训练径向基函数的方法。

一旦径向基函数完成训练，便使用协方差椭球体来设定定义三维表面的径向基函数的边界，从而绘制出三维表面。

因此，如上一节所述，径向基函数的结构及其经典训练算法已作介绍，而粒子群优化算法在本章1中已展示。下一小节将介绍计算协方差椭球体的方法。

3.3.1 协方差椭球

协方差椭球体是数据分布的一种几何表示。如果我们有一组点 x及其三维坐标 $(x_i, y_i, z_i)$，其中 i = 1,2,…,n，那么我们可以将协方差定义为

$$
\sigma(x, y) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \mu_x)(y_i - \mu_y). \tag{3.6}
$$

因此，协方差矩阵（公式(3.8)）包含了数据x的所有方差和协方差。

为了计算协方差椭球体，它是

需要计算该矩阵的特征值和特征向量。但首先，协方差矩阵必须使用逆‐χ‐平方分布进行缩放。上述过程是合理的，因为高斯随机变量的平方和服从卡方分布。卡方分布由“自由度”定义，自由度表示未知数的个数。在本例中，有三个未知数（椭球体的三个半轴），因此有三个自由度，如三维椭圆的公式(3.7)所示。

$$
\left( \frac{x}{\sigma_x} \right)^2 + \left( \frac{y}{\sigma_y} \right)^2 + \left( \frac{z}{\sigma_z} \right)^2 = s. \tag{3.7}
$$

因此，协方差椭球通过一个遵循卡方分布的值s进行缩放，我们必须通过将矩阵元素除以该值s的倒数来“消除”这个缩放因子。我们使用一个代表90%的s = 0.584值。

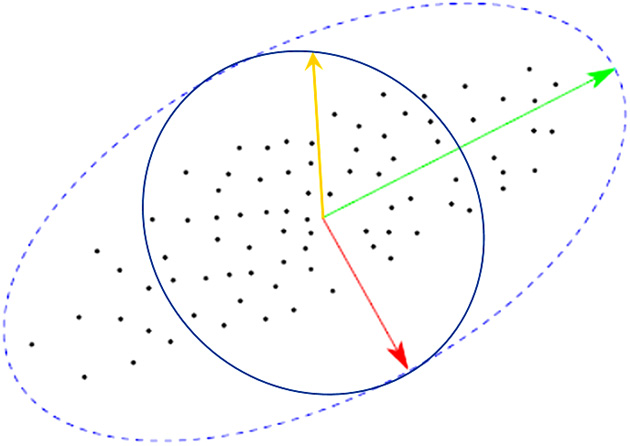
最后，特征向量表示椭球体半轴的单位向量。如果我们将这些向量按特征值的平方根进行缩放，就可以得到如图3.4所示的椭球体。

$$
\Sigma =
\begin{bmatrix}
\sigma(x, x) & \sigma(x, y) & \sigma(x, z) \
\sigma(y, x) & \sigma(y, y) & \sigma(y, z) \
\sigma(z, x) & \sigma(z, y) & \sigma(z, z)
\end{bmatrix}. \tag{3.8}
$$

我们可以使用缩放后的协方差矩阵公式 (3.8) 来计算马氏距离（公式 (3.9)）。该距离的计算成本低于欧几里得距离，并且可以让我们判断一个点位于椭球体内部（DM(x) < 1）还是外部（DM(x) > 1）。

$$
D_M(x’) = \sqrt{(x’ - \mu’)^T \Sigma^{-1} (x’ - \mu’)}. \tag{3.9}
$$

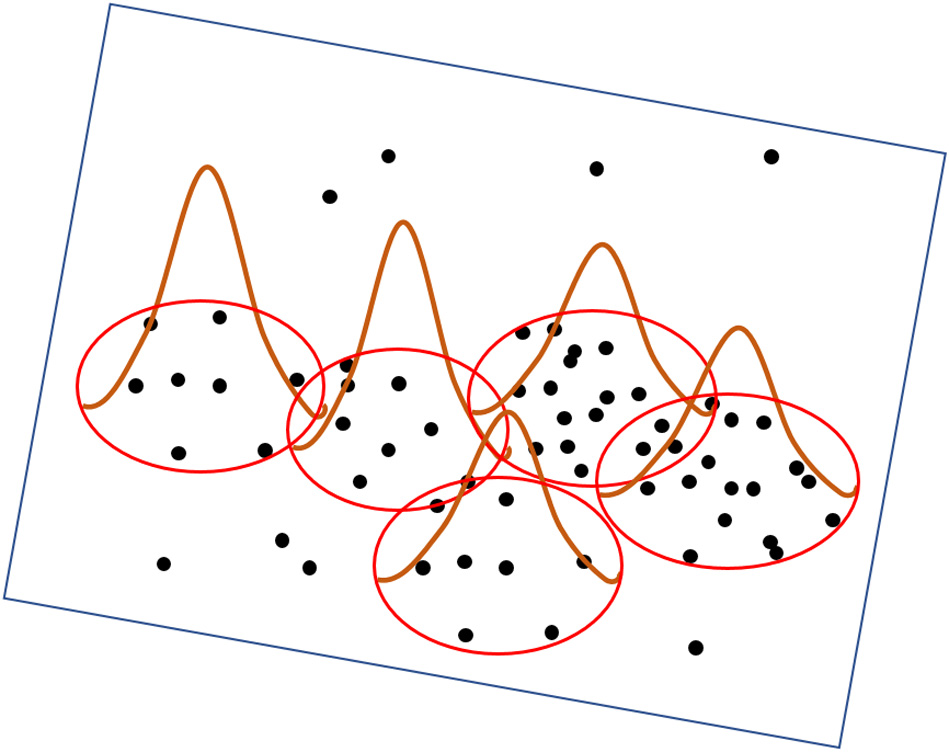
协方差椭球在人工智能的多个应用中被使用。在模糊逻辑中，用于建模隶属函数[3]。协方差椭球在解决映射任务时也很有用。例如，如果K‐means 被用作点云的分割算法，则所获得的簇可以用椭球体表示，如图3.5所示。

协方差椭球在解决映射任务时也很有用。例如，如果K‐means 被用作点云的分割算法，则所获得的簇可以用椭球体表示，如图3.5所示。

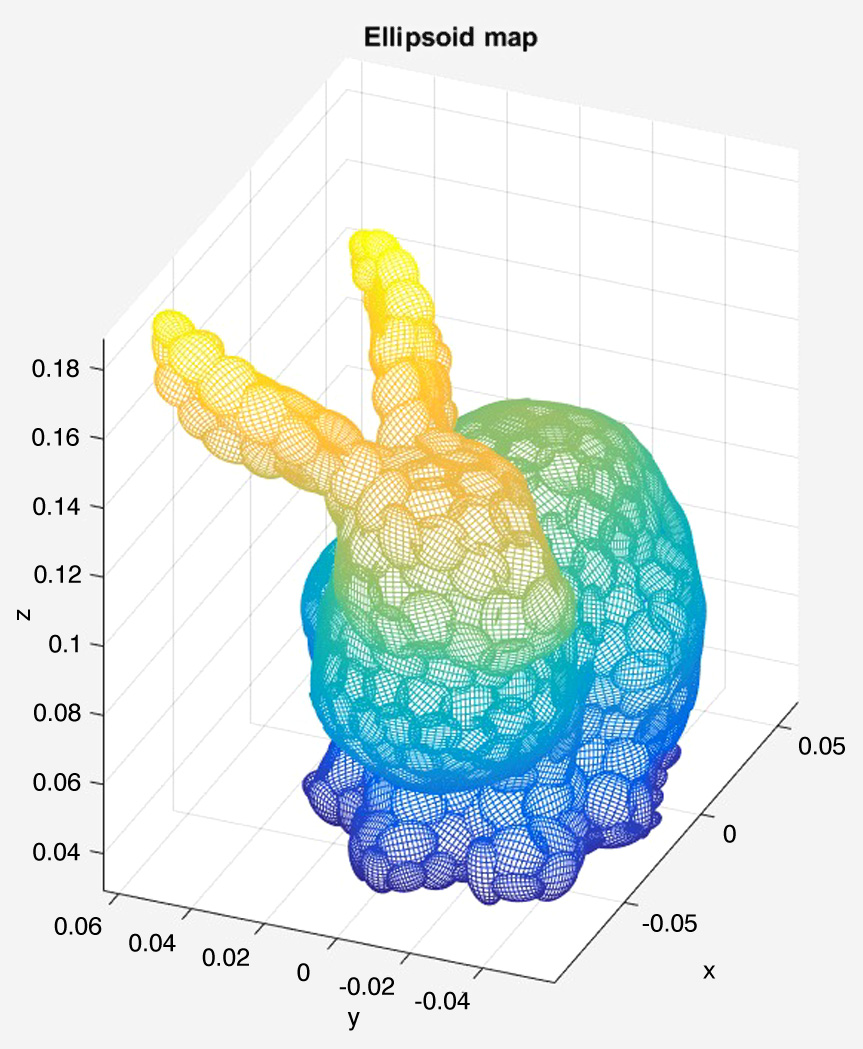
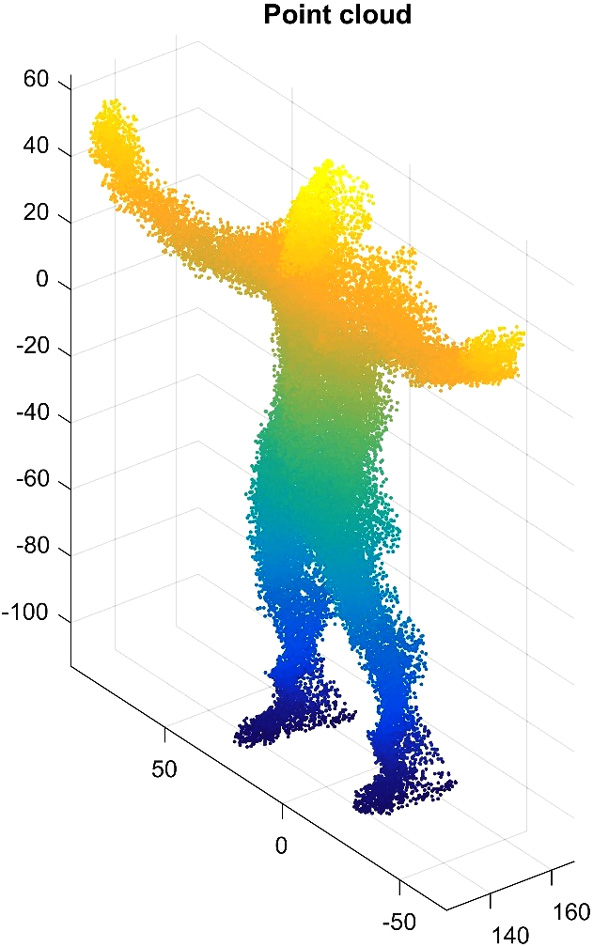
使用一个基准点云，即斯坦福兔子模型[5]如图3.6所示，并利用协方差椭球体获取其点云的簇。结果如图3.7所示。

3.3.2 RBF‐PSO与协方差椭球用于插值3D点云

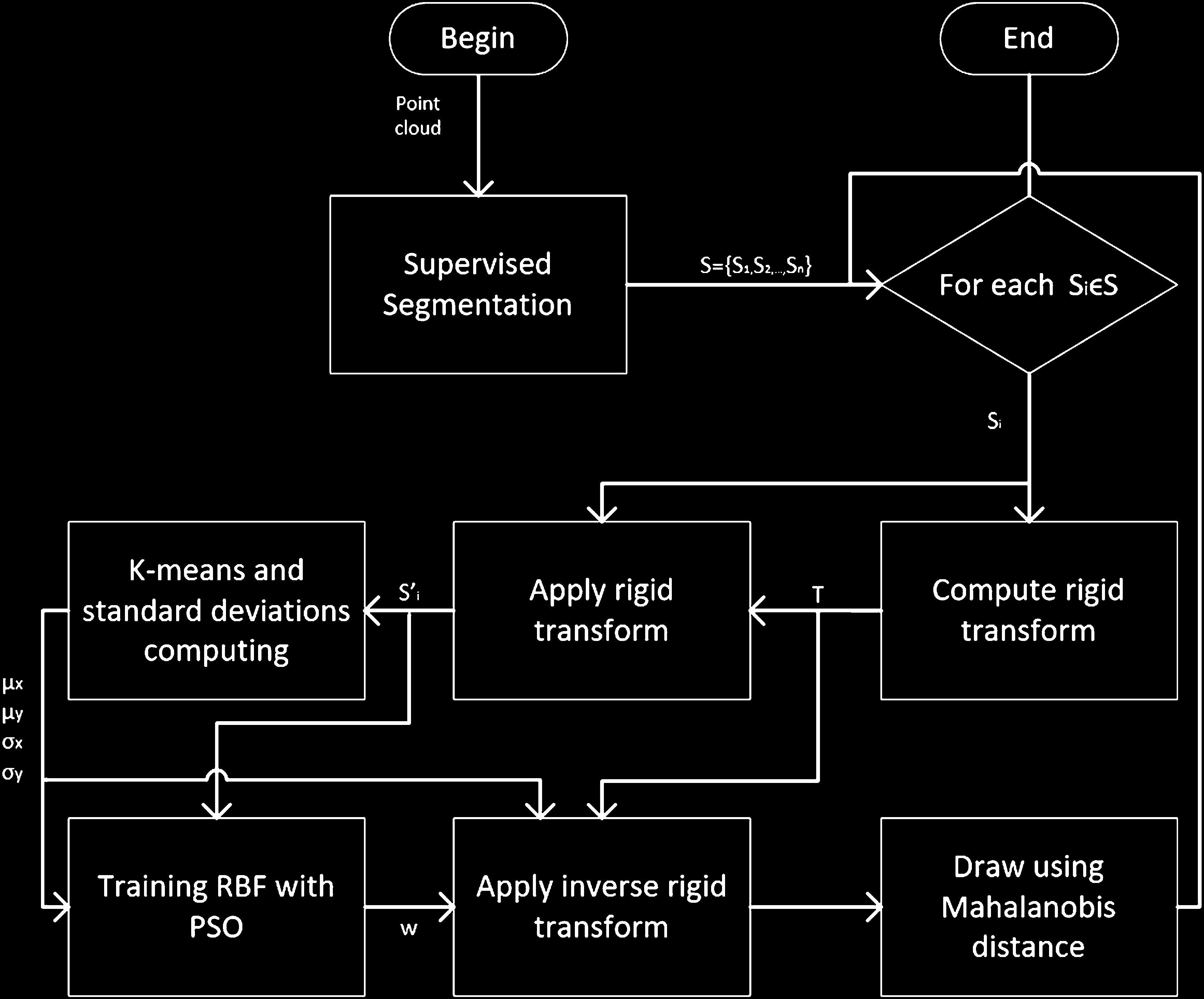
在本小节中，我们提出了一种用于解决从点云获取三维表面问题的算法。图3.8展示了我们方法的简化示意图。该过程的步骤描述如下：
1. 点云分割 。通过协方差椭圆以有监督的方式将点云分割成簇 $S_i$。进行有监督阶段是为了确保每个簇所包含的表面部分能够通过径向基函数的函数的线性组合进行近似。也就是说，每个协方差椭圆并且对其包含的点集进行测试，以确保由这些点描述的表面可以使用函数表面进行近似。

2. 刚性变换计算 。为了将分割的表面部分移动到公共坐标系中，需要计算一个刚性变换 $T=(R,t)$（旋转和平移变换）。

3. 使用 K‐means 和粒子群优化训练径向基函数 。每个径向基函数的中心 $\mu_x、\mu_y$ 和标准差 $\sigma_x、\sigma_y$ 通过 K‐means 确定。随后，使用与簇所用函数数量相等的粒子数以及公式 (3.10) 中的适应度函数，对径向基函数进行训练，以获得点云表面的插值。也就是说，我们调整训练集（输入点云）中每个点$(x_i、y_i、z_i)$的 $z$ 坐标。

4. 最后，绘制得到的表面 。使用在步骤1中计算出的刚性变换的逆变换 $T^{-1}=(R^T,-t)$ 以及马氏距离（公式(3.9)），绘制得到的插值表面。

形式上，在图3.9中，上述所描述的所提出算法的流程图如所示。

我们设计的粒子群优化（PSO）适应度函数，针对点云片段中的每个点$(x_i,y_i,z_i)$，其目标是最小化变换后点云的$z$坐标与径向基函数（RBF）在输入$(x,y)$下的估计输出之间的均方误差的平方根。可以在方程中看到

$$
f = \min_{w_1,w_2,\dots,w_k} \sqrt{ \frac{ \sum_{x’ \in S_i} \left( z - \sum_{j=1}^k w_j \exp\left( -\left[ \frac{(x-\mu_x)^2}{2\sigma^2} + \frac{(y-\mu_y)^2}{2\sigma^2_y} \right] \right) \right)^2 }{ |S_i| } }. \tag{3.10}
$$

3.3.3 实验结果

在本小节中，展示了实验结果。首先，给出了使用经粒子群优化训练的径向基函数进行2D基准函数逼近的实验结果。

这些实验旨在证明RBF‐PSO训练方法的有效性，之后我们设计了图3.8和图3.9 中所示的用于三维形状的方法。因此，我们所使用的适应度函数是方程(3.10)在降维情况下的简化版本。在这些实验中，对于二维函数逼近，目标是对函数中的每个点（以N个点采样）表面，最小化函数上该点的y坐标与径向基函数对输入x的估计输出之间的均方误差的平方根。这可以在以下方程中看出

$$
f = \min_{w_1,w_2,\dots,w_k} \sqrt{ \frac{ \sum_{i=1}^N \left( y - \sum_{j=1}^k w_j \exp\left( -\frac{(x-\mu_x)^2}{2\sigma^2} \right) \right)^2 }{ N } }. \tag{3.11}
$$

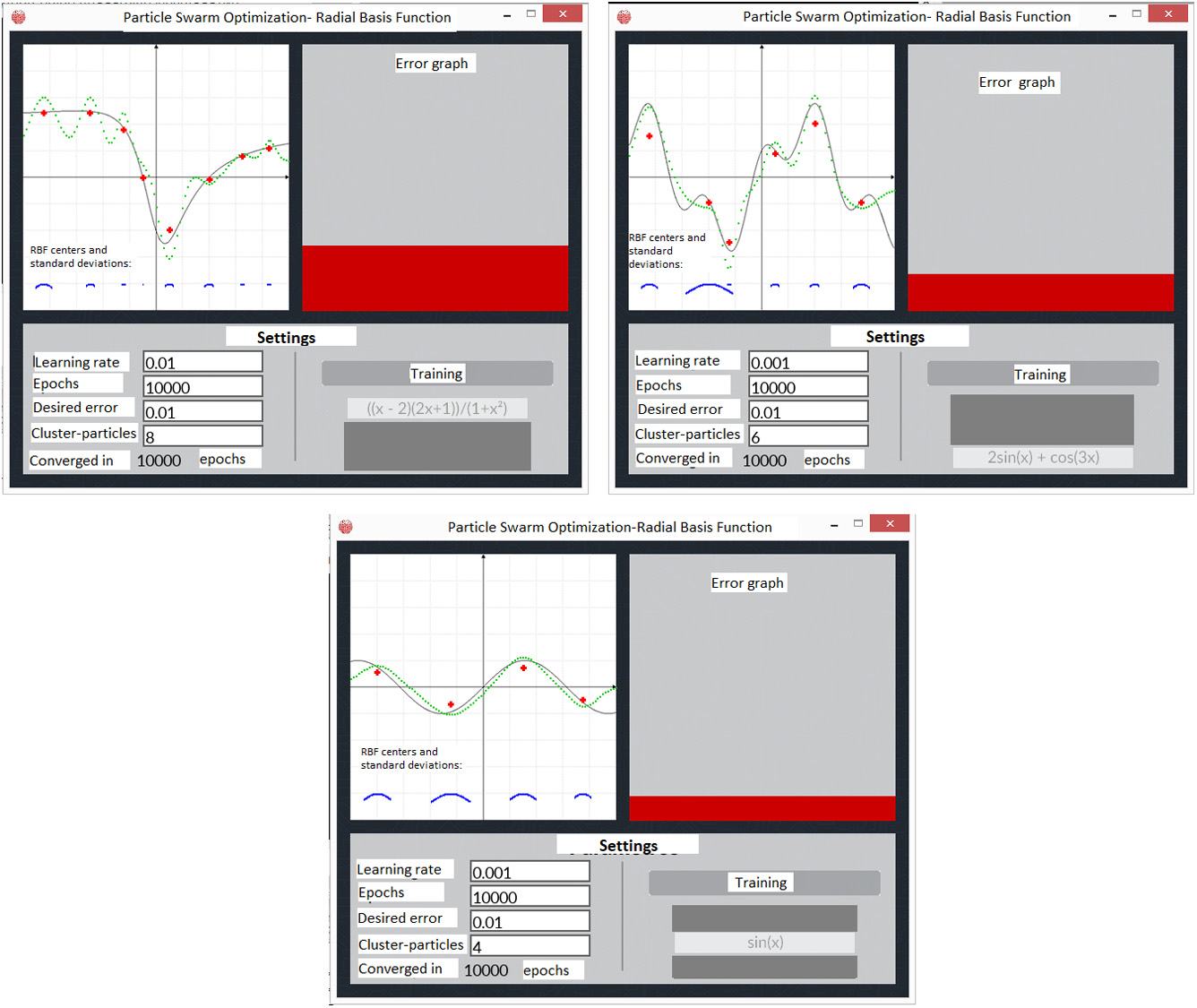
在图3.10中，展示了逼近三个二维基准函数的结果。函数曲面以实心黑线表示，逼近结果以虚线绿线表示。RBF中心和标准差在二维平面底部用蓝线表示。粒子的数量和最终位置对应于红色十字。每次实验的设置显示在每张图的底部。

正如读者所注意到的，每次实验使用较少的粒子（八个、六个和四个），每个函数的结果已经足够精确。这些简单但有前景的结果促使我们设计了图3.9中的方法来插值三维曲面。

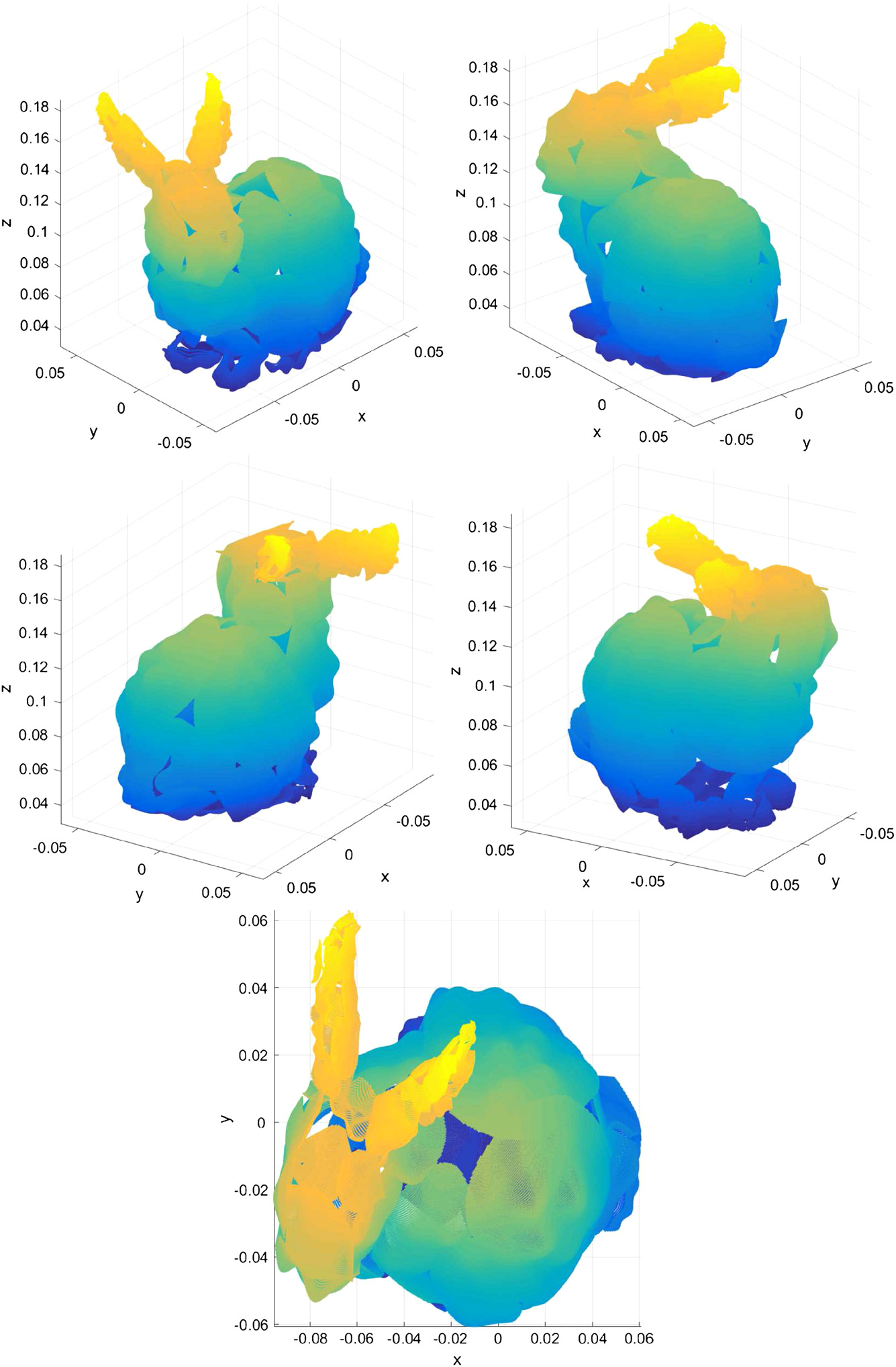
接下来，在图3.11中展示了使用我们的算法并以斯坦福兔子的点云作为输入数据所获得的三维表面的不同视图。该逼近使用了117个簇，每簇三个粒子，每个粒子代表一个径向基函数单元。需要强调的是，在我们过程的步骤1中，即使用协方差椭圆进行监督分割时，一些簇被舍弃了，因为它们的表面不满足作为函数的条件，因此无法计算使用径向基函数的插值。正因如此，在结果图中可以看到表面上存在一些孔洞。但另一方面，我们的曲面逼近过程比训练径向基函数的经典算法具有更低的计算复杂度，因为后者需要进行矩阵求逆运算。而粒子群优化则是计算每个粒子的两个线性方程，并且每个粒子可被视为一个子过程；在此情况下，即为解决整体问题一部分的一个线程。一旦每个子过程得到结果，就会将其与同级的结果进行比较，以改进未来结果。

由于每个粒子都可以独立评估，因此粒子群优化很容易实现并行化。该算法中仅在涉及变异以及选择最优个体的阶段才需要个体之间的通信。

SBSA实验中使用的每个径向基函数单元的误差如图3.12所示。

可以看出，前几个簇的逼近误差最大。这是因为这些簇在图中的点数多于最后几个簇（用径向基函数单元70及以上的簇进行逼近，见图3.12），而簇内的点数越少，获得的逼近误差就越小。

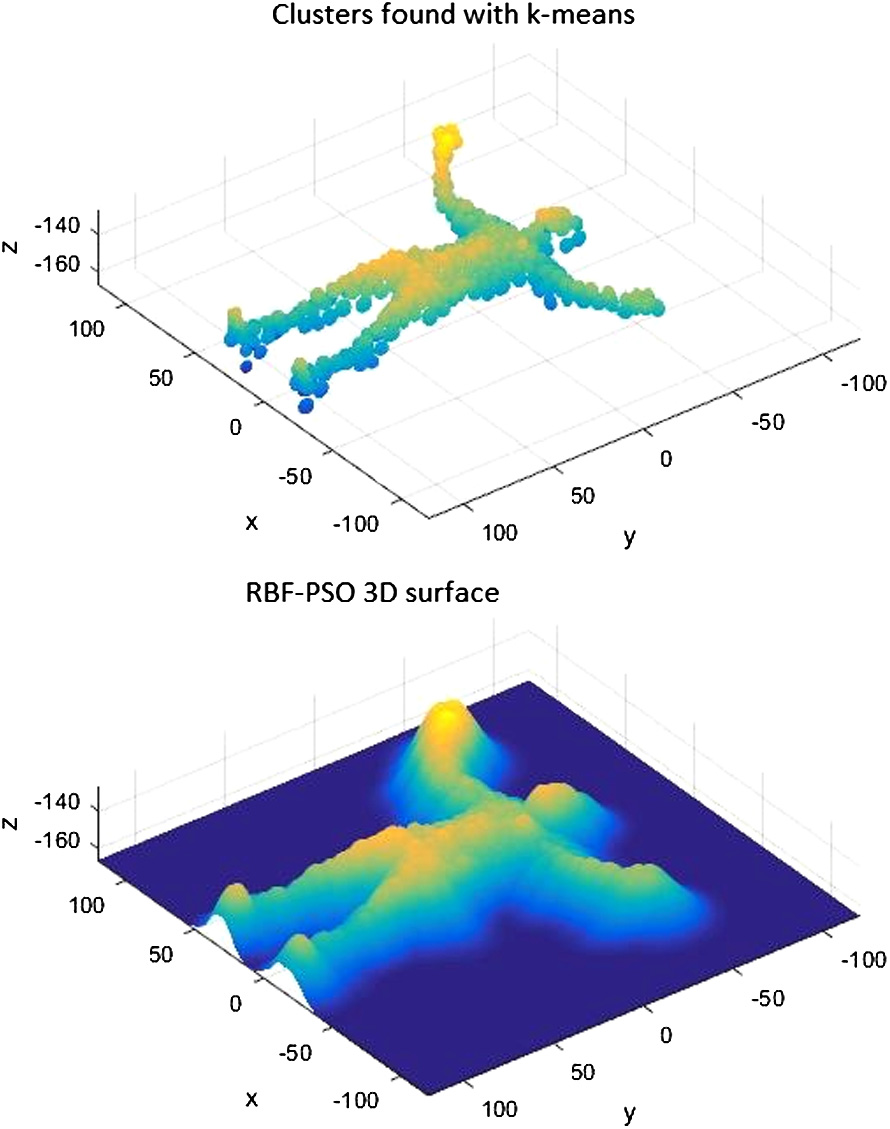
另一次实验结果使用了来自Acuity Technologies公司的 SRI‐500激光测距仪提供的点云作为输入，该设备能够扫描高达500英尺的距离，并以每秒80万个点的速度进行扫描。图3.13中所示点云包含的点数为794,917。通过K‐means获得的簇显示在图3.14的上半部分。在此实验中，没有簇被剔除，因为所有簇都满足作为函数表面的条件。这是由于这些簇具有较小的标准差，因此 RBF‐PSO近似的结果在表面上没有孔洞，如图3.14的下半部分所示。

3.4. 结论

本章提出了一种利用粒子群优化调整的径向基函数网络来逼近非结构化形状的算法。通过计算协方差椭圆，以确定定义三维表面的径向基函数的边界，并判断某一点是否位于椭球体内部或外部。

实验结果证明，该方法能够有效获得描述物体形状的三维曲面；尽管该算法未生成渲染后的形状，但所得到的表面可作为模式识别过程和环境建图的描述符。其原因在于该算法足够快速，可用于实时实现，满足机器人导航任务的需求。另一方面，使用3D点云描述形状时所需参数数量（点云中的点数 × 3）显著减少。例如，斯坦福兔子可以用117个径向基函数参数（$\mu_x,\mu_y, \sigma_x,\sigma_y$以及z坐标）来描述，而不是点云的362,272× 3个参数。

未来，我们将研究一种自主算法来分割点云，并测试片段中包含的表面是否满足替代我们流程中监督部分的函数的表面。这可以避免最终获得表面上出现孔洞，并有助于我们获取物体的渲染表面。