本文介绍了AVL平衡树的概念，为何需要它来避免搜索二叉树退化为链表，以及如何通过单旋和双旋实现节点的旋转。提供了AVL类的框架和插入函数，展示了如何通过调整平衡因子保持树的平衡性。
前言
1.为什么?为什么要有AVL平衡树
搜索二叉树(例如,左子树大 根 右子树小 中序遍历就能得到 降序数据)，比如依次插入2，3，1会得到如下 搜索二叉树：
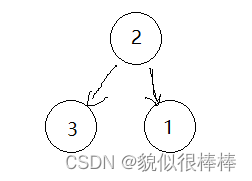
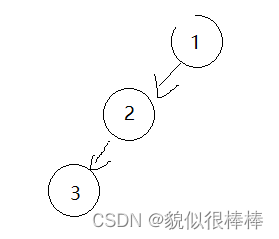
但形成的搜索树与插入值的顺序有关，在一些极端形况下会转换成单链表的存在形式，例如:依次插入3，2，1
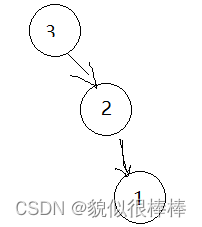
这就会导致实际上的搜索树退化成单链表，搜索效率从O（log N）退化成O（N），我们显然不想看到这样的结果！！
2.是什么?AVL平衡树是什么?
先说结论：AVL平衡树是解决了退化问题的搜索二叉树
我们如何解决搜索二叉树的退化问题？
如果我们有办法把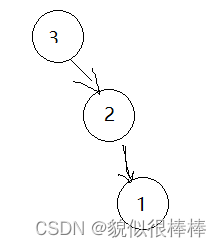
变成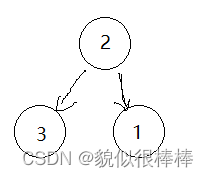
不就可以了，问题是我们怎么实现？
3.怎么做?怎么实现AVL平衡树?
3.1 单旋
首先我们给每一个节点定义一个平衡度 :这个平衡度的含义是这个节点的 右子树高度 与 左子树高度 之差。我们规定平衡度绝对值不能大于1。例如，对于节点3而言平衡度为2 显然是不平衡的。
平衡度==0：左右子树高度一样
平衡度==1：右子树 比 左子树 高 1个节点
平衡度==-1：左子树 比 右子树 高 1个节点
那么我们如何将3->2->1转变成3<- 2 ->1。答案是“左旋”（ps.自己想不到不要气馁，这本来就是历代计算机从业者的心血，能轻易想到才不正常，学就完事了）
对比一下我们就可以发现3成为2的左子树就行了，是的所谓“左旋”就是让3的右指向2的左，再让2的左指向3。这样我们会发现“旋转”的两个好处：
1. 3的平衡度改变了，3的平衡度从2变成了0
2 .整个树的高度降低了
ps. 与“左旋”对应的还有“右旋” -- “右旋” 与“左旋”与十分相似，在此不多赘述
“右旋”就是让1的左指向2的右，再让2的右指向3。
3.1 双旋
但是如果我们先插入2.5 再插入 2.8 会发生什么？
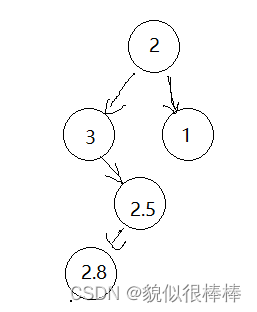
此时2的平衡度是-2，此时我们会发现无论是 对3进行左单璇：
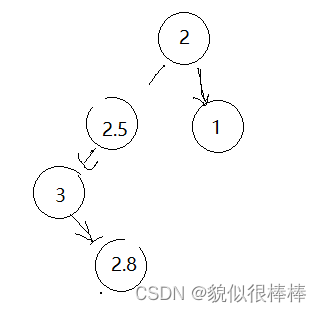
还是 对2 进行右单旋：
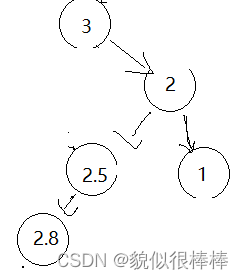
抑或其他节点的旋转，都无法解决问题：
因此我们引入了双旋：先让2.5右单旋 再让 3左单璇（右左单旋）
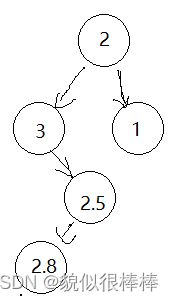
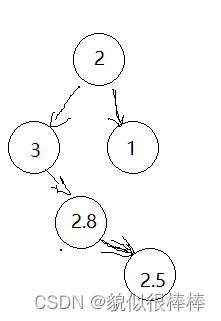
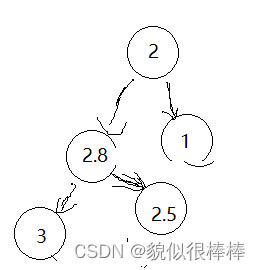
类似的有（左右单旋）不多赘述
代码实现
我们在此实现AVL的节点插入 与 检查 功能，目的在于学习AVL树旋转方面的知识
1.AVL类框架
首先我们我们的树节点必须包含以下部分：
1.存储的数据，在这里我用键值对pair
2.平衡因-- 每个节点的平衡度
3.左右子树节点指针
4.父亲节点指针（方便找到自身节点的父亲节点 有助于代码书写）
#pragma once
#include <iostream>
#include <assert.h>
using namespace std;
template<class K,class V>
struct Node
{
pair<K, V> _data;
int _bf;//平衡因子
Node<K, V>* _left;
Node<K, V>* _right;
Node<K, V>* _parent;
//constructor
Node(const pair<K, V> val = pair<K, V>())
: _data(val)
, _bf(0)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
{}
};
//默认左小右大
template<class K,class V>
class AVL
{
public:
typedef Node<K,V> _Node;
//构造函数
AVL()
:_root(nullptr)
{}
~AVL()
{
_delete(_root);
}
private:
//析构函数内部函数
bool _delete(_Node* root)
{
if (root == nullptr) return true;
_delete(root->_left);
_delete(root->_right);
delete root;
}
private:
_Node* _root;
};
2.AVL树insert函数实现（节点旋转 单旋 双旋）
bool insert(const pair<K,V>& val)
{
_Node* new_Node = new _Node(_Node(val));
if (_root == nullptr)
{
_root = new_Node;
return true;
}
//find insert position and relative parent position
_Node* parent = nullptr;
_Node* cur = _root;
while (cur != nullptr)
{
parent = cur;
if (cur->_data.first < val.first)
cur = cur->_right;
else if (cur->_data.first > val.first)
cur = cur->_left;
else//该元素的键值已经存在
return false;
}
//insert the element
if (parent->_data.first < val.first) parent->_right = new_Node;
else parent->_left = new_Node;
new_Node->_parent = parent;
//balence
cur = new_Node;
while (parent != nullptr)
{
//adjust parent's balance factor : _bf
if (parent->_right == cur) ++parent->_bf;
else --parent->_bf;
if (parent->_bf == 0) //插入该节点后父亲平衡了 说明原本父亲节点缺 左/右节点 插入的节点正好为 右/左节点 树的高度没变 不会向上影响
return true;
else if (parent->_bf == 1 || parent->_bf == -1)//原本父亲节点没有左右节点 插入后改变了树的高度 会向上影响
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)//通过旋转调整parent 使其恢复插入前的高度 因此不会向上影响
{
if (parent->_bf == 2 && cur->_bf == 1) leftRotate(parent);
else if (parent->_bf == 2 && cur->_bf == -1) right_leftRotate(parent);
else if (parent->_bf == -2 && cur->_bf == -1) rightRotate(parent);
else if (parent->_bf == -2 && cur->_bf == 1) left_rightRotate(parent);
else
{
cout << "insert error: rotate error " << endl;
assert(false);//其他情况不应该存在 如果存在则说明整个逻辑不对
}
break;//不用再向上调整了
}
else//error : bf > -2 || bf > 2
{
cout << "insert error: bf > -2 || bf > 2 " << endl;
return false;
}
}
return true;
}
//rotate function
bool rightRotate(_Node* parent)
{
_Node* pParent = parent->_parent;
_Node* subL = parent->_left;
_Node* subLR = subL->_right;
parent->_left = subLR;
if(subLR != nullptr) subLR->_parent = parent;
subL->_right = parent;
parent->_parent = subL;
subL->_parent = pParent;
if (_root == parent) _root = subL;
else
(pParent->_left == parent) ? (pParent->_left = subL) : (pParent->_right = subL);
subL->_bf = 0;
parent->_bf = 0;
return true;
}
bool leftRotate(_Node* parent)
{
_Node* pParent = parent->_parent;
_Node* subR = parent->_right;
_Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL != nullptr) subRL->_parent = parent;
subR->_left = parent;
parent->_parent = subR;
subR->_parent = pParent;
if (parent == _root)//pParent == nullptr parent为根节点
_root = subR;
else
(pParent->_left == parent) ? (pParent->_left = subR) : (pParent->_right = subR);
parent->_bf = 0;
subR->_bf = 0;
return true;
}
bool left_rightRotate(_Node* parent)
{
_Node* subL = parent->_left;
_Node* subLR = subL->_right;
int bf = subLR->_bf;
//双旋转调整
leftRotate(parent->_left);
rightRotate(parent);
//平衡因子调整
subLR->_bf = 0;
if (bf == 0) subL->_bf = parent->_bf = 0;
else if (bf == 1)
{
parent->_bf = 0;
subL->_bf = -1;
}
else if (bf == -1)
{
parent->_bf = 1;
subL->_bf = 0;
}
else
{
cout << "left_rightRotate error" << endl;
assert(false);
}
return true;
}
bool right_leftRotate(_Node* parent)
{
_Node* subR = parent->_right;
_Node* subRL = subR->_left;
int bf = subRL->_bf;
//双旋转调整
rightRotate(parent->_right);
leftRotate(parent);
//平衡因子调整
subRL->_bf = 0;
if (bf == 0)
{
parent->_bf = 0;
subR->_bf = 0;
}
else if (bf == 1)
{
subR->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1)
{
subR->_bf = 1;
parent->_bf = 0;
}
else
{
cout << "right_leftRotate" << endl;
assert(false);
}
return true;
}
3.AVL检查（检查一棵树是不是AVL树）
bool isAVL_Tree()//判断该树是不是AVL树
{
return isSearchTree() && isBalance();
}
bool isSearchTree()//判断一棵树是不是搜索二叉树 即 左小 右大
{
return _isSearchTree(_root);
}
bool isBalance()//判断该树每个节点是否平衡
{
return _isBalance(_root);
}
bool _isSearchTree(_Node* root)//判断一棵树是不是搜索二叉树 即 左小 右大
{
if (root == nullptr) return true;
if (root->_left && (*root) < *(root->_left))
{
cout << "root > root->left:";
cout << "[" << root->_data.first << "," << root->_data.second << "]";
cout << ">";
cout << "[" << root->_left->_data.first << "," << root->_left->_data.second << "]";
cout << endl;
return false;
}
if (root->_right && (*root) > *(root->_right))
{
cout << "root < root->right:";
cout << "[" << root->_data.first << "," << root->_data.second << "]";
cout << "<";
cout << "[" << root->_right->_data.first << "," << root->_right->_data.second << "]";
cout << endl;
return false;
}
return _isSearchTree(root->_left) && _isSearchTree(root->_right);
}
int _TreeHeight(_Node* root)//计算一棵树的高度
{
if (root == nullptr) return 0;
return max(_TreeHeight(root->_left), _TreeHeight(root->_right)) + 1;
}
bool _isBalance(_Node* root)
{
if (root == nullptr) return true;
int leftHeight = _TreeHeight(root->_left);
int rightHeight = _TreeHeight(root->_right);
int difHeight = rightHeight - leftHeight;
if (difHeight < -1 || difHeight > 1)
{
cout << "[" << root->_data.first << "," << root->_data.second << "]";
cout << "root balance error:";
cout << endl;
cout << "root balance:" << difHeight;
cout << "root left balance:" << leftHeight;
cout << "root balance:" << rightHeight;
cout << endl;
return false;
}
if (difHeight != root->_bf)
{
cout << "[" << root->_data.first << "," << root->_data.second << "]";
cout << "root balance save error:";
cout << "bf should be: " << difHeight << "notshould be: " << root->_bf << endl;
}
else return _isBalance(root->_left) && _isBalance(root->_right);
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
