优化算法目录:http://t.csdnimg.cn/75T9p
一、注意事项
1.1 C++17
由于框架中涉及目录的创建,与目录极其内容的清理。因此需要调用C++17才开始提供的库—文件系统filesystem。
visual studio如何设置C++17与文件系统(其实就是文件夹)的使用可参考连接:C++17 filesystem 文件系统(详解)-优快云博客
1.2 适应度函数(重要)
在进行使用之前,一定要先自己编写好适应度函数!!!!
本系列系统的框架只认适应度越大越好的情况。因此当你想求解的问题是适应度越小越好时需要转换你的适应度函数。转换方法有很多,我这里提两个。
1.现适应度函数值等于 = -原适应度函数值
2.现适应度函数值等于 = 1/原适应度函数值(当适应度可能计算为0时 会存在除零问题)
编写格式:
double 函数名(const individual& 个体名)
{
//个体一维度特征 个体名[0];个体二维度特征 个体名[1]
return 个体名[0];
}
//示例:我设定函数名为fit_func 个体名为which_one
//想求X1^2 + X2^3 = 8 的解
//因此解的维度有两个 目的是让解代入X1^2 + X2^3与8的距离越小越好
//因此适应度为 -abs(维度1^2 + 维度2^3 - 8)
double fit_func(const individual& which_one)
{
double fitness = -abs(pow(whcih_one[0],2) + pow(whcih_one[1],3) - 8);
return fitness;
}1.3 边界条件
当用户输入的边界条件与用户输入的个体维度不相符时,有以下三种情况:
1.一个解有n个维度,而用户输入的每个解的边界条件大于n个时:程序会报错终止
2.一个解有n个维度,而用户输入的每个解的边界条件等于n个时:程序正常运行
3.一个解有n个维度,而用户输入的每个解的边界条件小于n个时:程序会将最后一个边界作为填充物,补足解的边界条件至n。
如果不明白可以看下面的情况分析:
//想求X1^2 + X2^3 + X3^9= 8 的解
情况1:
//X1取值范围是0~1 X2取值范围是0~5 X3取值范围是0~4
//用户输入下边界{0,0,0,0} 上边界应该是{1,5,4,5}
//此时程序报错
情况3:
//X1 X2 X3取值范围是0~1
//下边界就应该是{0} 上边界应该是{1}
//程序会自动补充为{0,0,0} 与 {1,1,1}
//X1 取值范围是0~1 X2 X3 3~4
//下边界就应该是{0,3} 上边界应该是{1,4}
//程序会自动补充为{0,3,3} 与 {1,4,4}
1.4 结果查找
默认在你当前工作目录下Run_and_Save_Result的文件夹里
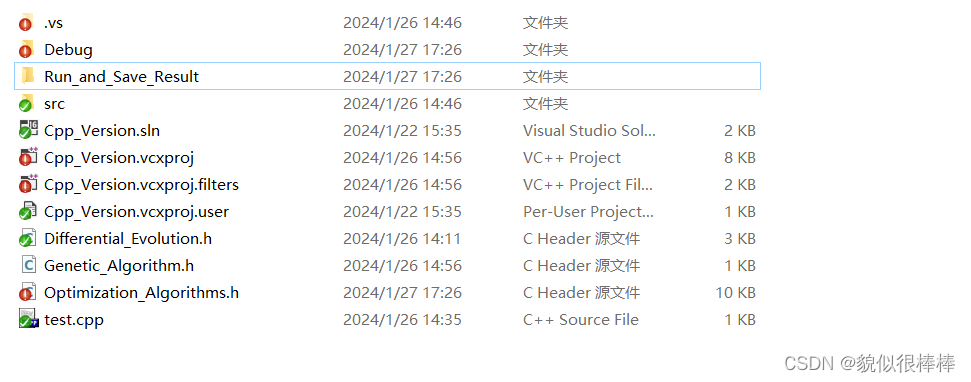

实在不知道当前工作目录在哪可以用这种方式:

二、快速上手使用
2.1 使用方法
以visual studio使用为例:
step1:从优化算法目录跳转到gitee代码

step2:下载算法zip
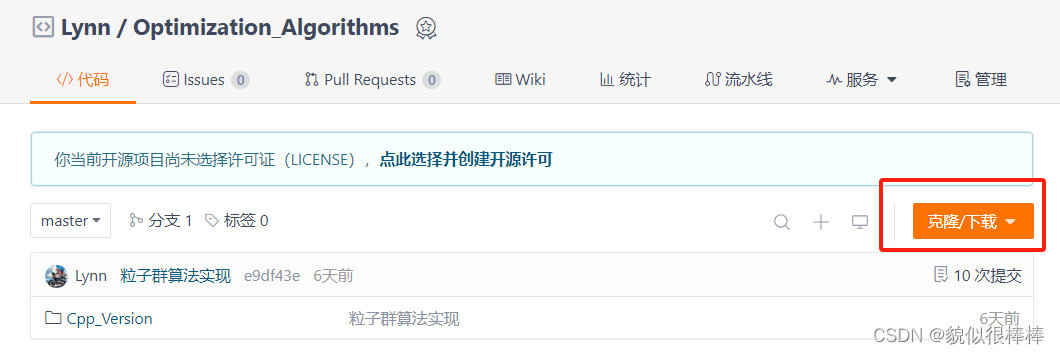
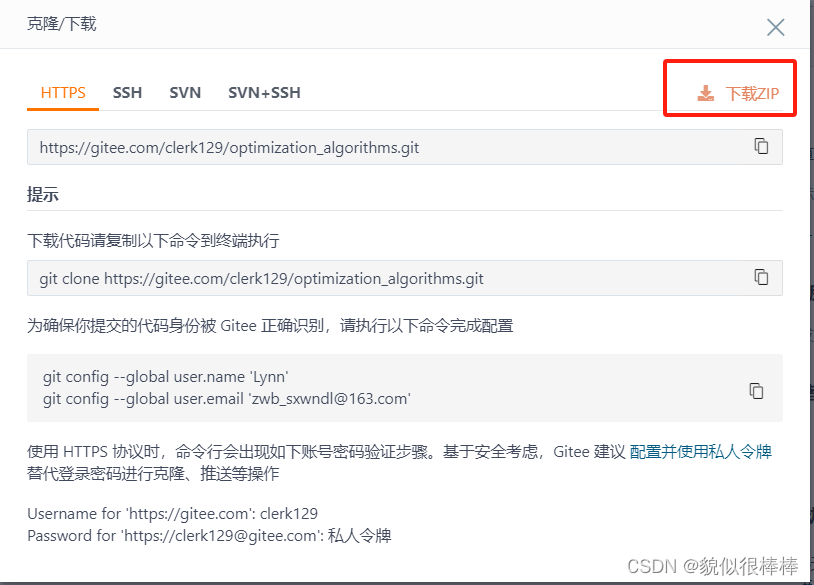
step3:创建visual studio项目
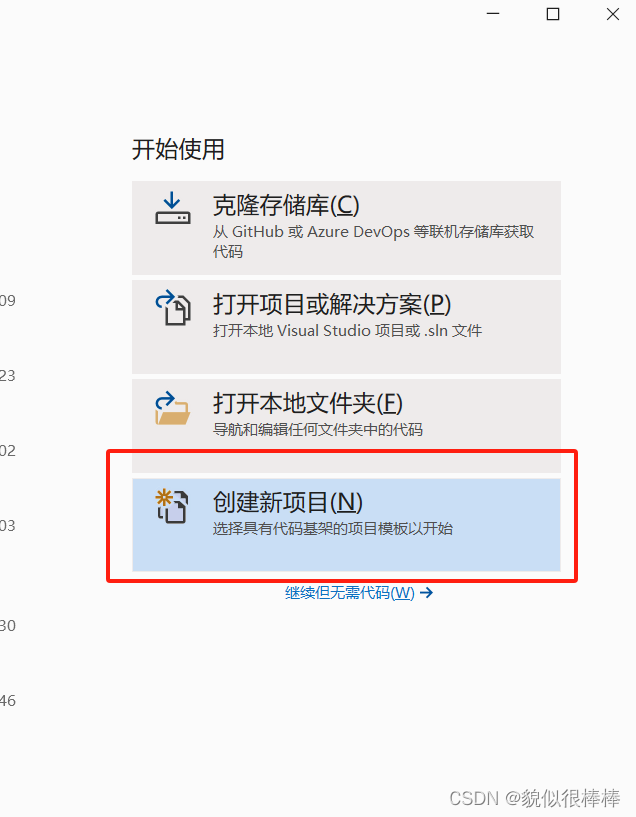
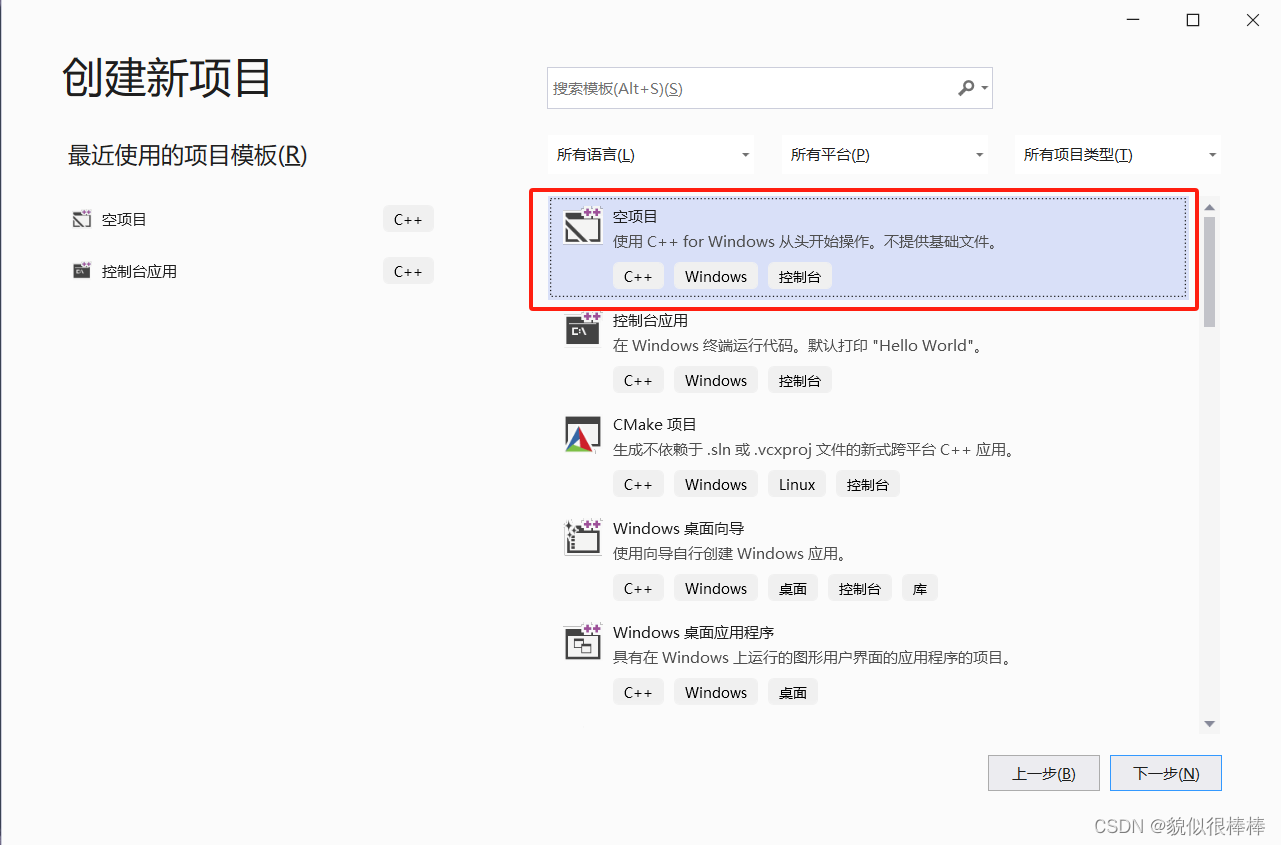
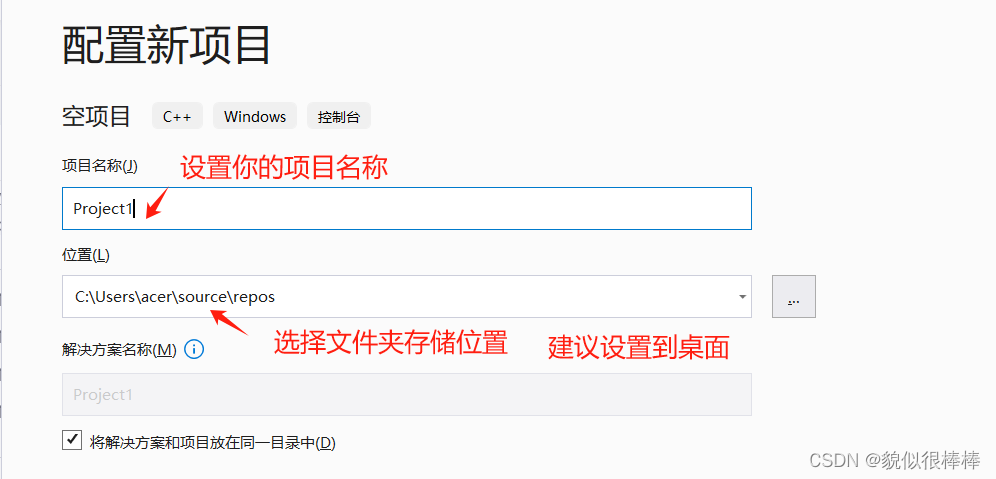
step4:将步骤2下载的算法拷贝到步骤3新建的项目中
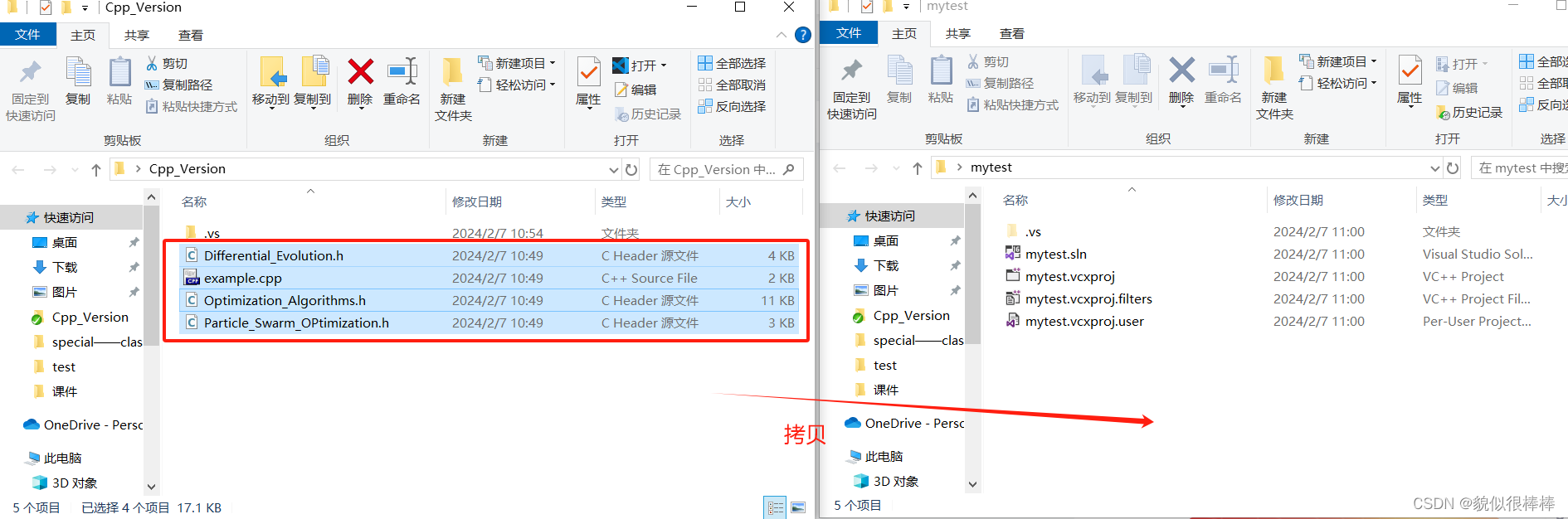
step5:在visual中添加算法
先打开资源管理器,再添加头文件与测试文件现有项
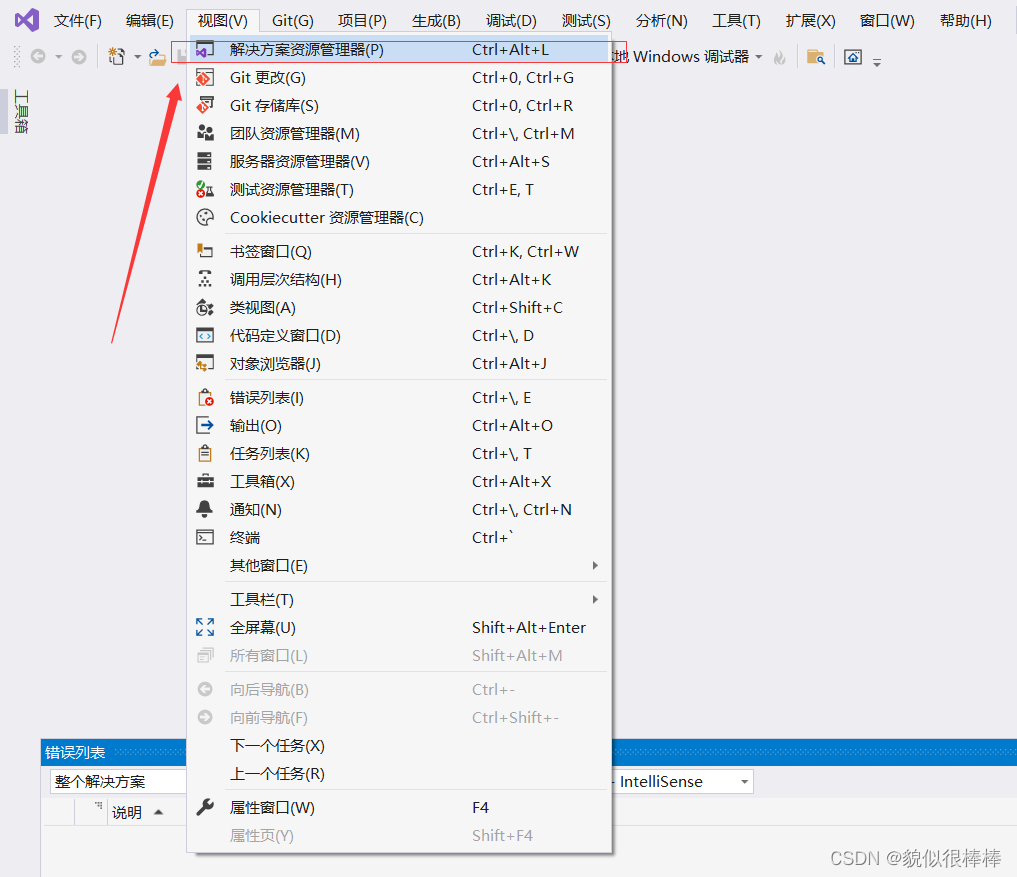
添加头文件(.h文件)
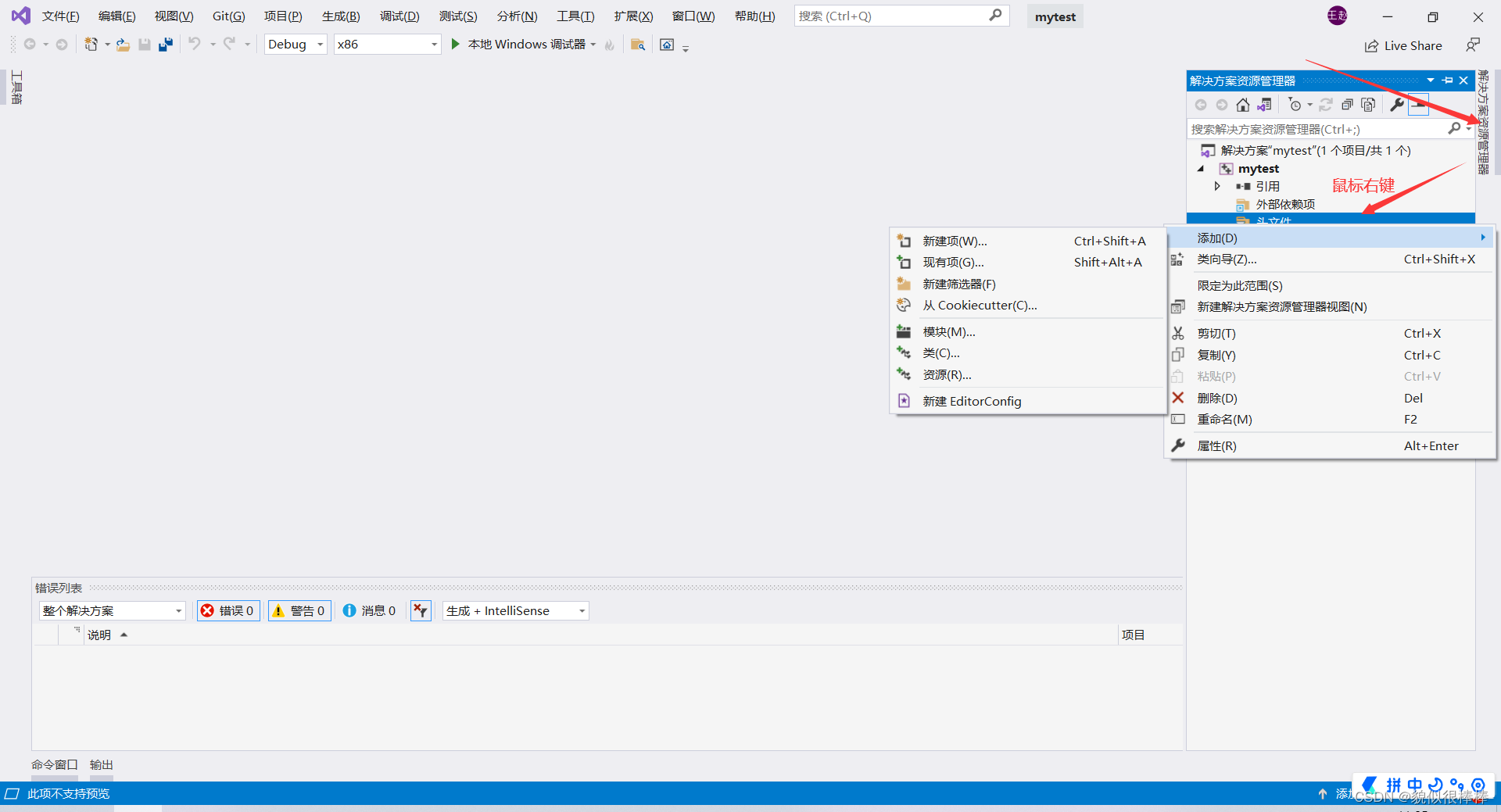
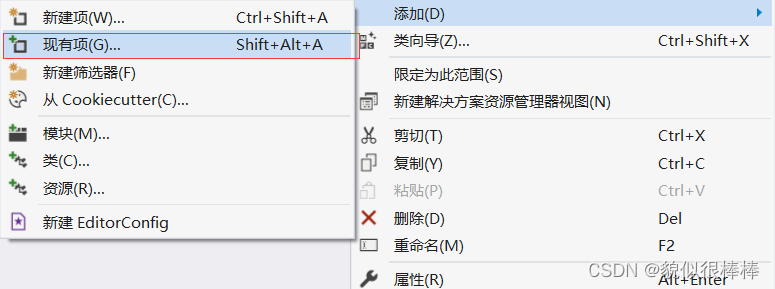
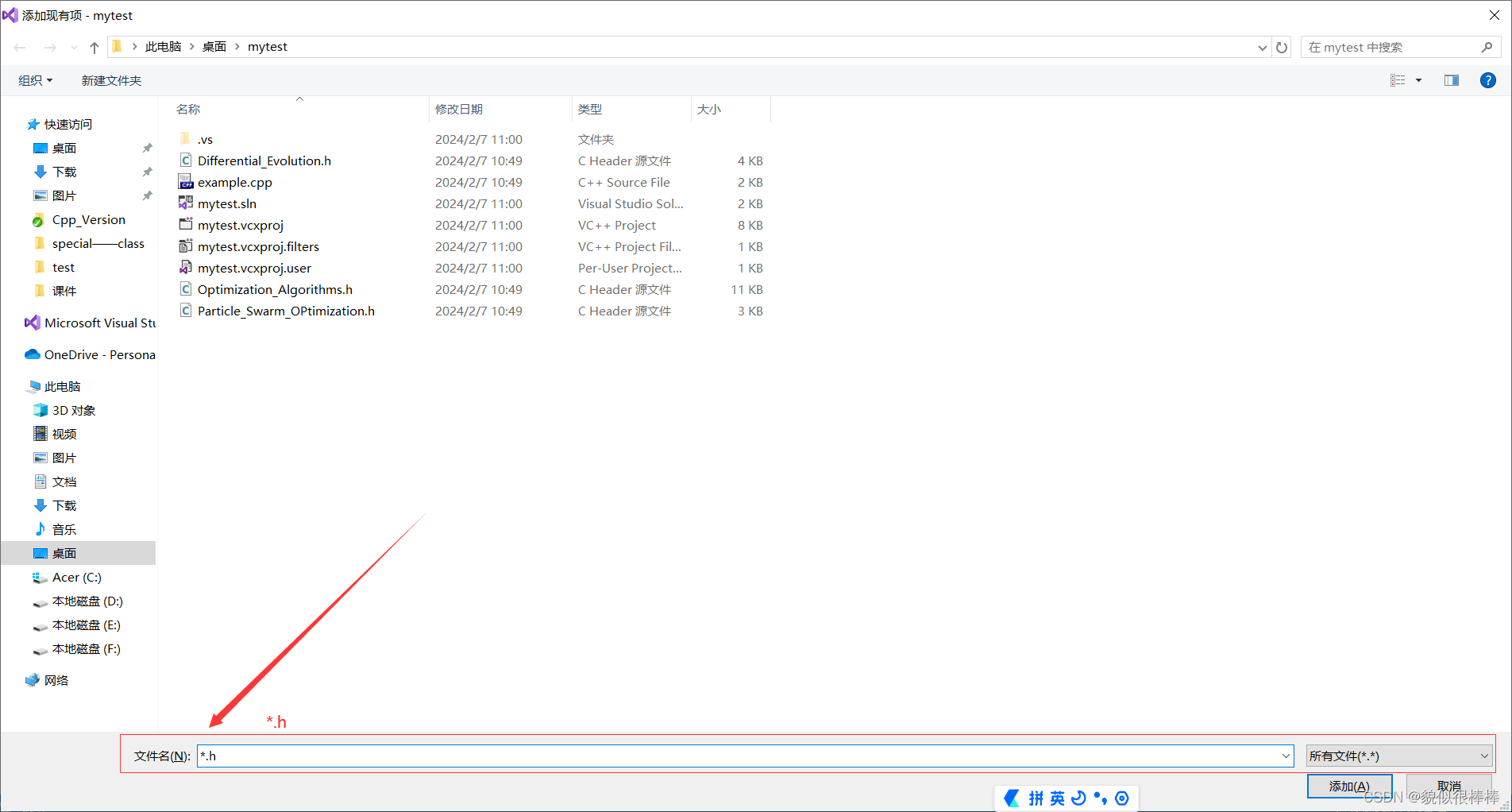
添加源文件现有项(.cpp文件)
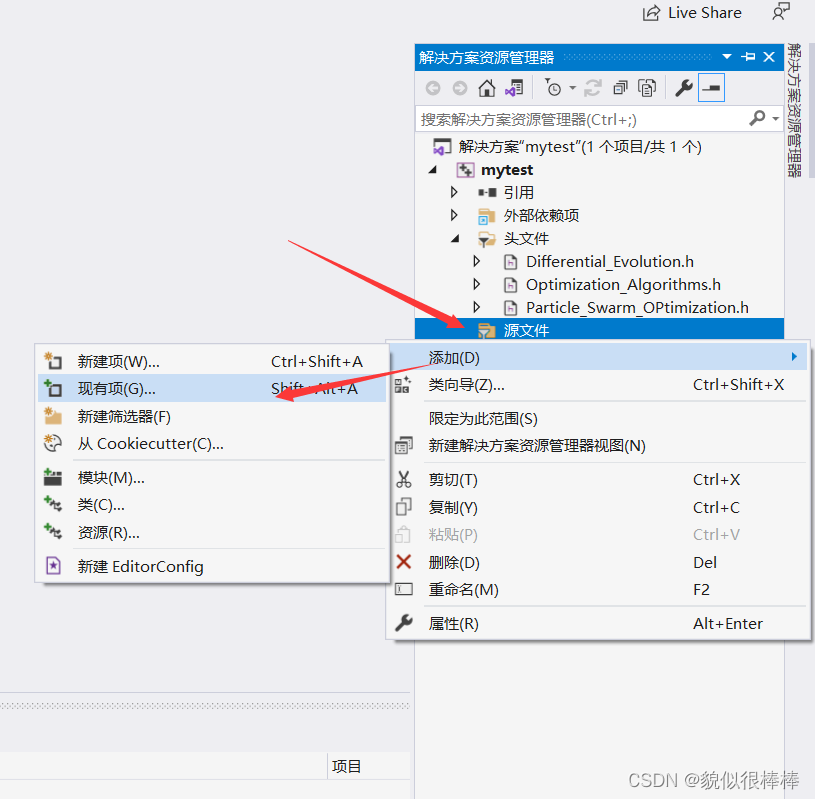
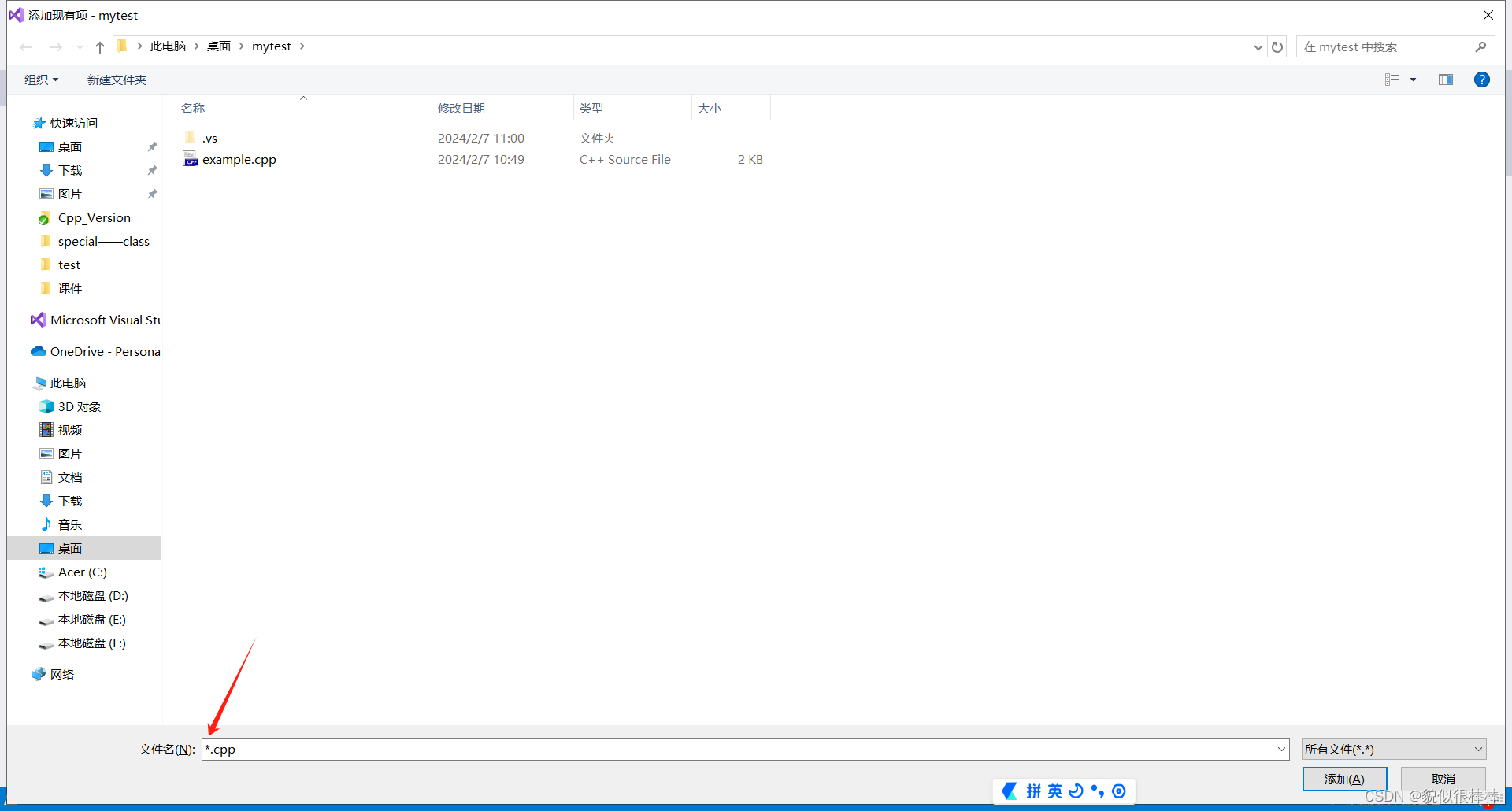
step5:结束
如果你双击打开文件后,显示如下错误:
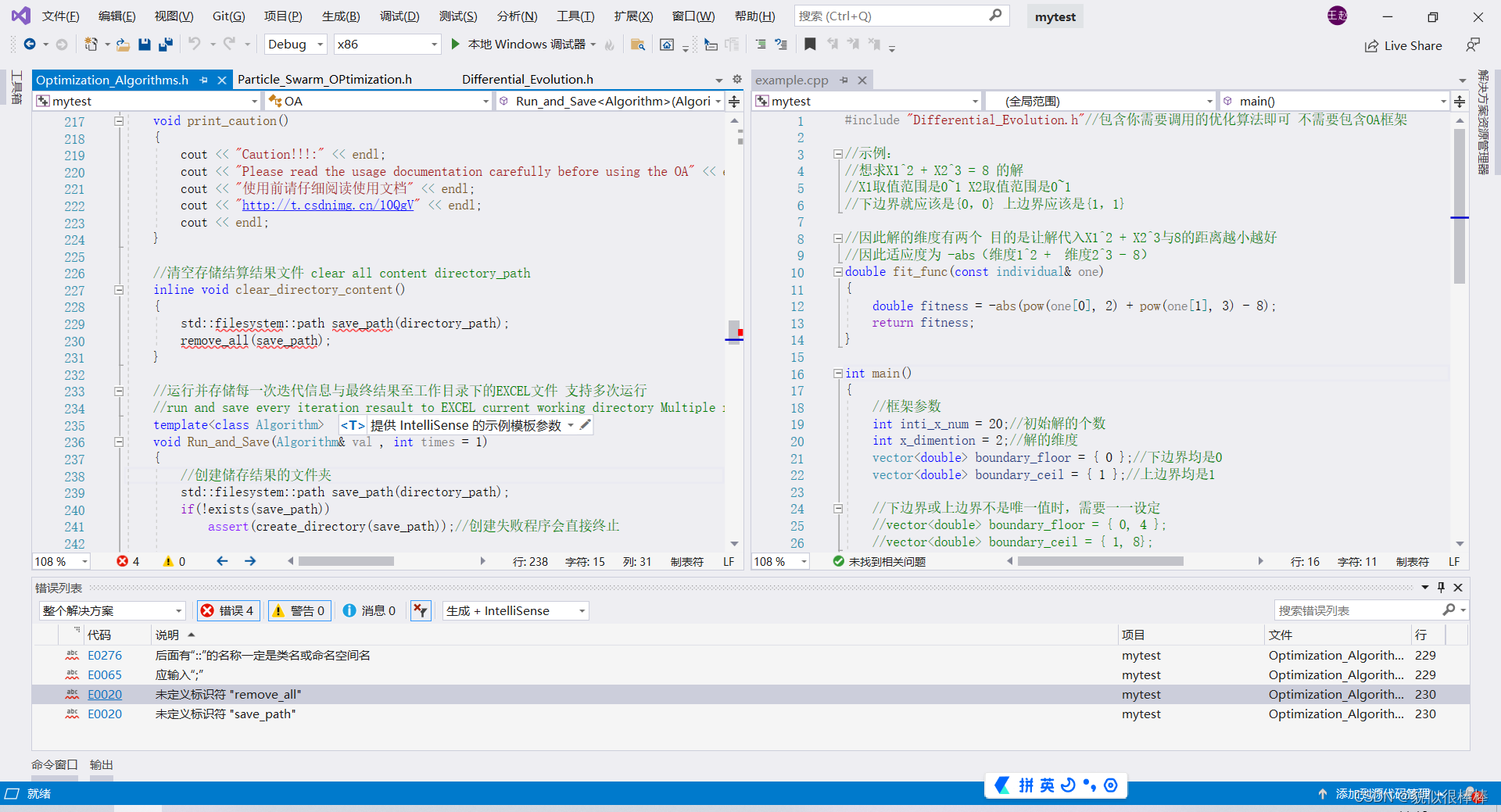
那说明你没支持C++17,按照本文1.1节的内容设置即可
2.2 代码调用
以差分进化(DE,differential evolution)的调用作为示例:
#include "Differential_Evolution.h"//包含你需要调用的优化算法即可 不需要包含OA框架
//示例:
//想求X1^2 + X2^3 = 8 的解
//X1取值范围是0~1 X2取值范围是0~1
//下边界就应该是{0,0} 上边界应该是{1,1}
//因此解的维度有两个 目的是让解代入X1^2 + X2^3与8的距离越小越好
//因此适应度为 -abs(维度1^2 + 维度2^3 - 8)
double fit_func(const individual& one)
{
double fitness = -abs(pow(one[0], 2) + pow(one[1], 3) - 8);
return fitness;
}
int main()
{
//框架参数
int inti_x_num = 20;//初始解的个数
int x_dimention = 2;//解的维度
vector<double> boundary_floor = { 0 };//下边界均是0
vector<double> boundary_ceil = { 1 };//上边界均是1
int max_iterator = 100;//最大迭代次数
//DE算法参数
double F = 0.5;
double cr = 0.3;
//调用模板
OA frame(fit_func, inti_x_num, x_dimention, boundary_floor, boundary_ceil, max_iterator);
DE de(frame, F, cr);
//清空存储结果的文件,放在运行前面可以把上次运行的结果清理掉
frame.clear_directory_content();
//运行并保存结果 结果可在当前工作目录查找
frame.Run_and_Save(de,10);
return 0;
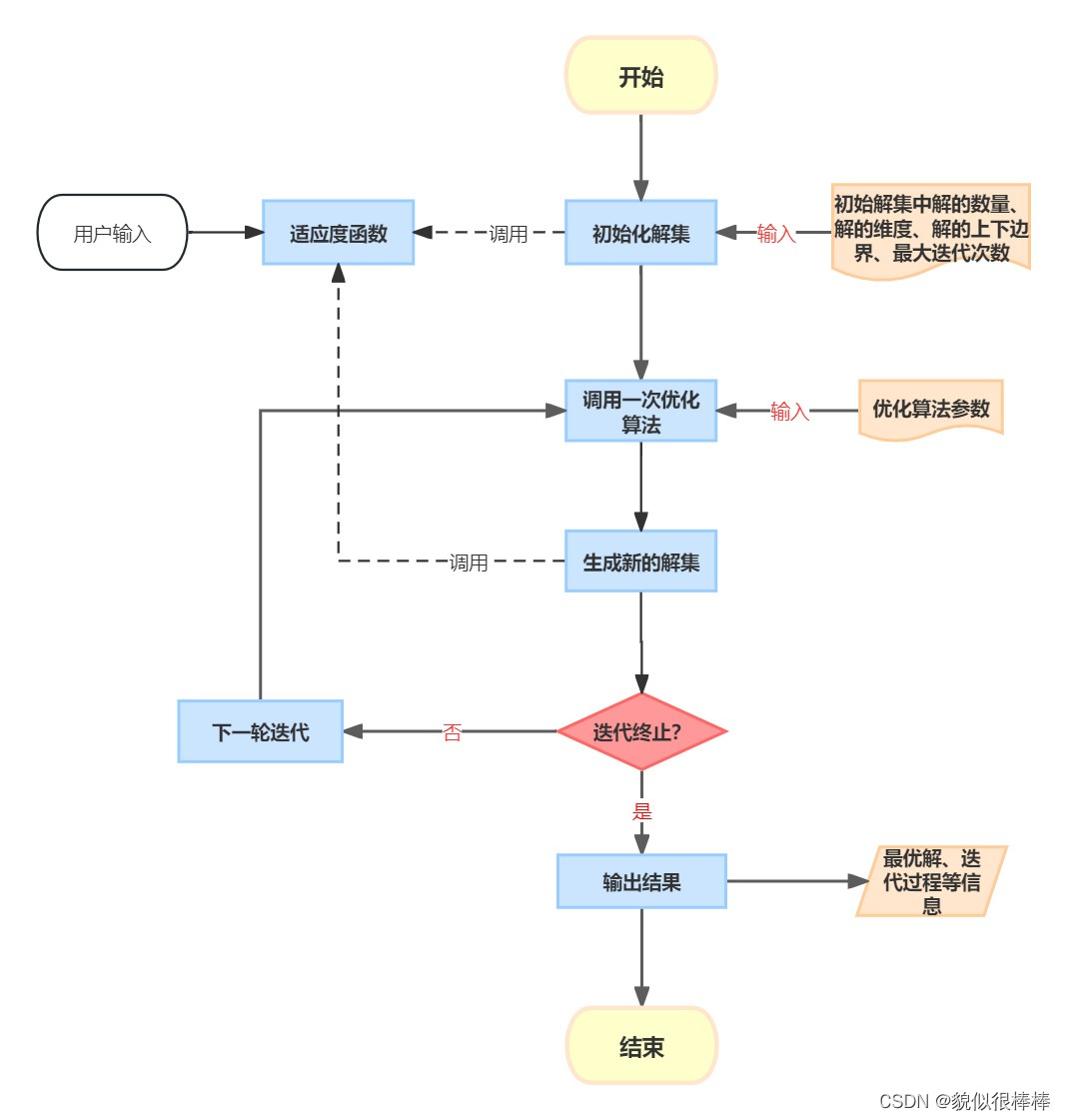
}首先用户根据自己要解决的问题设定好自己的适应度函数、解的维度与边界条件。再根据一些经验设定初始解的个数、最大迭代次数。同时选好要用的优化算法。
之后应用OA类创建一个对象,用上述提到的设定好的参数对对象进行初始化。
再之后根据选定的优化算法,确定算法参数,构建算法对象,初始化算法对象的时候第一个参数一定要填上一步创建好的OA类对象,不然程序会报错终止。
要是你想快速知道你想用的算法有哪些参数可以在目录查询哦。
最后用OA类创建的对象调用Run_and_Save()函数,填充优化算法对象,就可以直接进行迭代计算了,每一步的迭代结果会存在1.4展示的文件里。同时屏幕会给你输出,最优的(整个迭代过程中适应度最高的)迭代结果,及其对应的适应度值。当然,如果你想一次性执行10次优化算法,只需要frame.Run_and_Save(de,10);这样调用就可以了。这样结果就出来了:
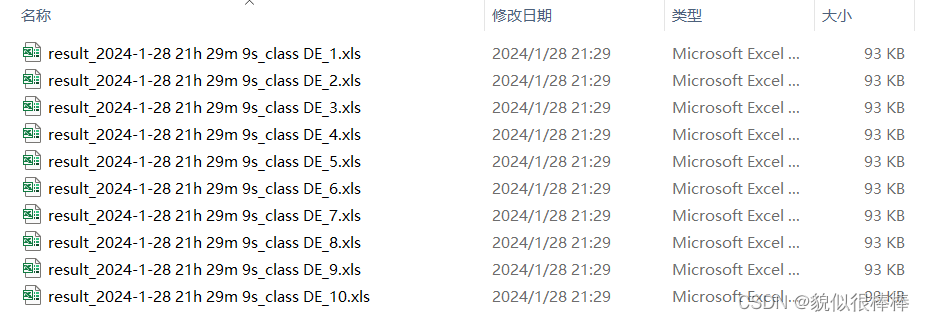

要注意的是,只要你调用了这个算法,计算机就会给你存储结果,你调用几次就存储几个EXCEL文件如果你觉得之前的结果不重要了,记得手动清理文件(直接把文件夹删了就行)或者调用frame.clear_directory_content();函数来给你打工^_^。
三、框架设计思想(Optimization_Algorithms.h的设计思路)
不是很好写,emmm,随缘更新吧,主要是想说框架是怎么设计的为什么要这么设计 以及一些别的东西,这块是深入了解了,如果你想更改我的源码或者写自己的算法可以看看,简单使用的话倒也不必看了。
3.1 individual类
3.2 OA类
四、框架函数 (实时更新)

4.1 void clear_directory_content(void);
函数功能:清空存储运算结果的文件及文件夹
4.2 void compute_population_fitness(void);
函数功能:计算并更正当前解的适应度
4.3 void make_in_boundary(individual& val);
函数功能:检查一个解的每一个维度值是否在对应边界条件内,如果不在,就将其替换为更接近的边界
4.4 void print_caution(void);
函数功能:打印注意事项 打印优化算法目录的网页连接
4.5 template<class Algorithm>
void Run_and_Save(Algorithm& val , int times = 1)
函数功能:运行times次对应的Algorithm算法(用户自己选择的算法),并输出结果




 本文介绍了如何在C++17环境中使用一个优化算法库,包括设置适应度函数、处理边界条件、调用差分进化算法DE,并提供了使用步骤和框架设计思想。
本文介绍了如何在C++17环境中使用一个优化算法库,包括设置适应度函数、处理边界条件、调用差分进化算法DE,并提供了使用步骤和框架设计思想。
















 435
435

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








