动态规划之背包问题

动态规划（dynamic programming）是一种高级的算法，其求解过程中的每一个状态一定是由上一个状态推导出来的，这区别于贪心算法，贪心没有状态推导，而是从局部直接选最优的。动态规划求解问题中比较有名的就是背包问题，当然其能够求解的问题有很多，下面就是可以利用动态规划求解的一些问题（题目源自leetcode，题单来自于代码随想录）

1.背包问题概述

背包问题的分类主要是同一物品的数量不同带来的，分类情况如下图所示：这些背包问题还可以组合形成混合背包问题，大家可以去搜索“背包九讲”查看更加详细的背包问题资料

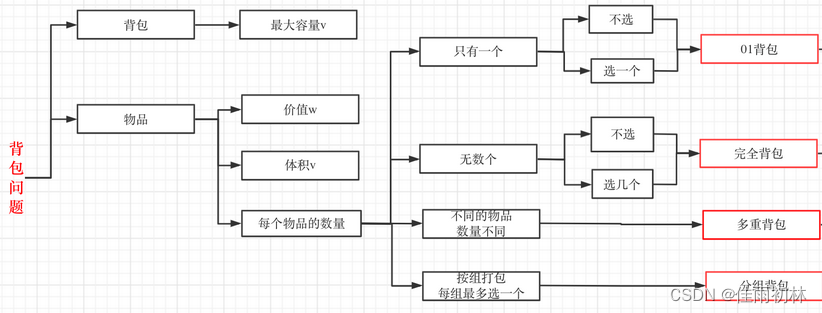
2. 0-1背包问题

2.1 0-1背包问题模板

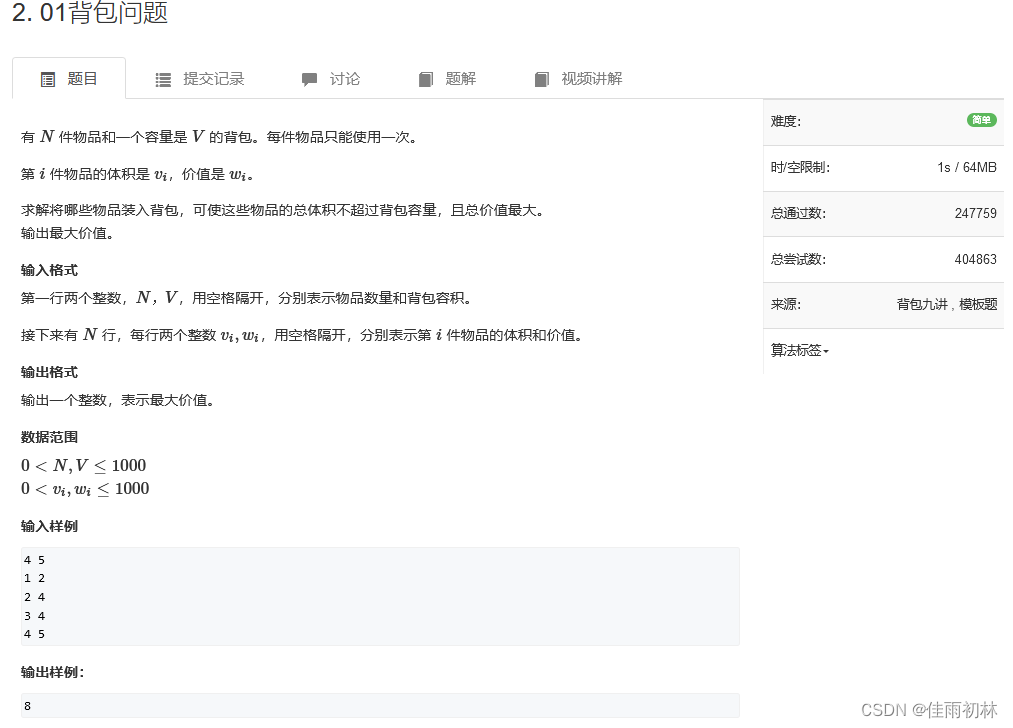
0-1背包问题有一个很明显的特征就是每件物品只有一件，这也就是说我们如果选择了这个物品，之后这个物品就没有了。我们用一个二维数组dp来存储状态，只有物品0时，背包容积逐渐增大所能够达到的最大值，接着又多了一个物品1时，背包容积逐渐增大所能够达到的最大值，以此类推最终得到n个物品背包最大体积所能够创造的最大值。（以下面的三个物品，背包容量为4的情况为例子）

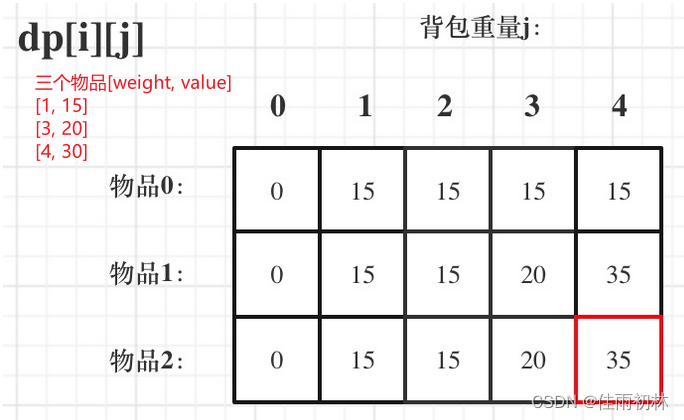
采用二维数组dp存储时，需要先初始化dp数组，此时先两层for循环实现的先后顺序可以调换（先遍历物品还是先遍历背包空间都可以），不过建议外层遍历物品，内层遍历空间，这样好理解一些。遍历先后顺序的核心代码对比：

// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) {
   
    // 遍历物品
    for(int j = 0; j <= bagweight; j++) {
   
    // 遍历背包容量
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

    }
}
//==================================
// weight数组的大小 就是物品个数
for(int j = 0; j <= bagweight; j++) {
   
    // 遍历背包容量
    for(int i = 1; i < weight.size(); i++) {
   
    // 遍历物品
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

0-1背包题解实现：（模板题）

#include <iostream>
#include<vector>
using namespace std;

int main(){
   
   
    int n, volumn;//n是物品数量，volume是背包体积
    cin>>n>>volumn;
    vector<vector<int>> item(n, vector<int>(2));
    for(int i = 0; i < n; i++){
   
   
        //输入物品的体积和价值[体积，价值]
        cin>>item[i][0]>>item[i][1];
    }
    vector<vector<int>> dp(n, vector<int> (volumn + 1, 0));
    //初始化dp数组，数组第一行（也就是第一个物品），当背包容积能够装下物品的时候，dp[i][j]就要改成物品一的价值
    for(int j = volumn; j >= item[0][0]; j--){
   
   
        dp[0][j] = item[0][1];//初始化第一行，能够放下第一个物品时候，dp[0][j]的价值就为物品一的价值
    }
    //开始0-1背包过程:外层i为物品数量，内层j为背包体积
    for(int i = 1; i < n; i++){
   
   
        for(int j = 0; j <= volumn; j++){
   
   
            if(j < item[i][0]){
   
   //背包体积容不下物品i时，就无需考虑价值变化
                dp[i][j] = dp[i - 1][j];//其最大价值还是体积大小为j，上个一物品时的最大价值
            }else{
   
   
                //背包能够容下物品i，这个时候就需要考虑将物品i加入背包了（最大价值变大了就加入）
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - item[i][0]] + item[i][1]);
            }
        }
    }
    cout<<dp[n - 1][volumn];
    
    return 0;
}

上面的代码可以进行空间优化，我们发现每一行的所取到的价值只和上一行最大价值有关，所以我们可以将dp[][]优化为一维dp[]（这里我们从尾到头更新最大价值，这样就不影响我们使用上一行的数据）,代码的实现过程如下：

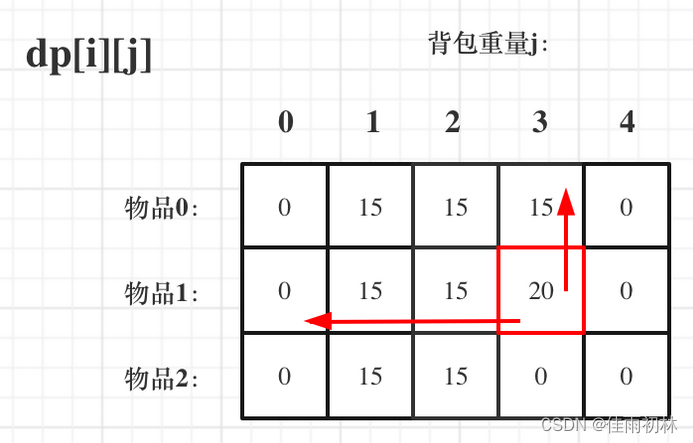
此时一维数组dp的时候，一定是外层遍历物品，内层遍历背包大小的顺序，不能够够调换

#include <iostream>
#include<vector>
using namespace std;

int main(){
   
   
    int n, volumn;//n是物品数量，volume是背包体积
    cin>>n>>volumn;
    vector