贪心算法笔记

正如这个算法的名字一样，解决题目的时候用一种贪婪的思想来解决问题，比如说我们要从一堆钞票中取3张，并且总和要最高，所以我们在遍历这堆钞票价值的时候，尽可能地选择炒面面值最高的，这样就得到了最终解。所以，贪心的思路就是利用每一个阶段的最优解，最终达到全局最优解。下面的题目是一些利用贪心解决的算法问题，题目列表来源代码随想录入口

1.序列问题

1.1摆动序列

解法一：贪心

class Solution {
   
   
public:
    int wiggleMaxLength(vector<int>& nums) {
   
   
        if(nums.size() <= 1) return nums.size();
        int curDiff = 0; //当前一对差值
        int preDiff = 0; //前一对差值
        int result = 1; //记录峰值个数，序列默认序列最右边有一个峰值
        for(int i = 0; i < nums.size() - 1; i++){
   
   
            curDiff =nums[i + 1] - nums[i];
            //出现峰值
            if((preDiff <= 0 && curDiff > 0) || (preDiff >=0 && curDiff < 0)){
   
   
                result++;
                preDiff = curDiff;
            }
        }
        return result;
    }
};

解法二：动态规划

class Solution {
   
   
public:
    //动态规划实现：dp[i][0]表示第i个数作为山峰的摆动子序列的最长长度
    //动态规划实现：dp[i][1]表示第i个数作为山谷的摆动子序列的最长长度
    int dp[1005][2];//这个大小是根据题目给出数值的范围来定义的
    int wiggleMaxLength(vector<int>& nums) {
   
   
        memset(dp, 0, sizeof dp);
        dp[0][0] = dp[0][1] = 1;
        for(int i = 1; i < nums.size(); i++){
   
   
            dp[i][0] = dp[i][1] = 1;
            for(int j = 0; j < i; j++){
   
          
                if(nums[j] > nums[i]) dp[i][1] = max(dp[i][1], dp[j][0] + 1);
            }
            for(int j = 0; j < i; j++){
   
   
                if(nums[j] < nums[i]) dp[i][0] = max(dp[i][0], dp[j][1] + 1);
            }
        }
        return max(dp[nums.size() - 1][0], dp[nums.size() - 1][1]);
    }
};

1.2单调递增的数字

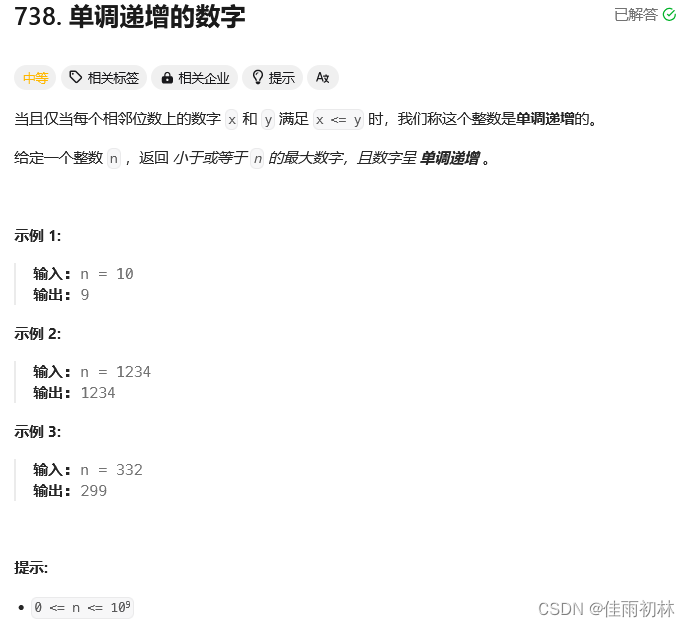
这个题目如果我们暴力循环求解的话，会出现超时报错，所以我们采用构建的方式的，利用单调递增且数字尽可能大这两个条件来构建我们的答案数字。
实现思路：
例如：98，一旦出现strNum[i - 1] > strNum[i]的情况（非单调递增），首先想让strNum[i - 1]–，然后strNum[i]给为9，这样这个整数就是89，即小于98的最大的单调递增整数
从前向后遍历的话，遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]减一，但此时如果strNum[i - 1]减一了，可能又小于strNum[i - 2]。
这么说有点抽象，举个例子，数字：332，从前向后遍历的话，那么就把变成了329，此时2又小于了第一位的3了，真正的结果应该是299。
那么从后向前遍历，就可以重复利用上次比较得出的结果了，从后向前遍历332的数值变化为：332 -> 329 -> 2998

class Solution {
   
   
public:
    int monotoneIncreasingDigits(int n) {
   
   
        string strNum = to_string(n);
        //flag用来标记赋值9从哪开始
        //设置为这个默认值，为了防止第二个for循环在flag没有被赋值的情况下执行
        int flag = strNum.size();
        for(int i = strNum.size() - 1; i > 0; i--){
   
   
            if(strNum[i - 1] > strNum[i]){