递归相关题目笔记

递归，是分治策略的一个具体实现，通过将一个大问题分解为同样的小问题，逐层分解到边界之后，再向上“归”，最终得到整个问题的答案。

1.二叉树相关递归问题

二叉树的节点的定义：

//=========================C++版本========================
/** 
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
//==================Java版本====================
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 //=====================python版本=======================
//# Definition for a binary tree node.
//# class TreeNode(object):
//#     def __init__(self, val=0, left=None, right=None):
//#         self.val = val
//#         self.left = left
//#         self.right = right

1.1 二叉树的最大深度

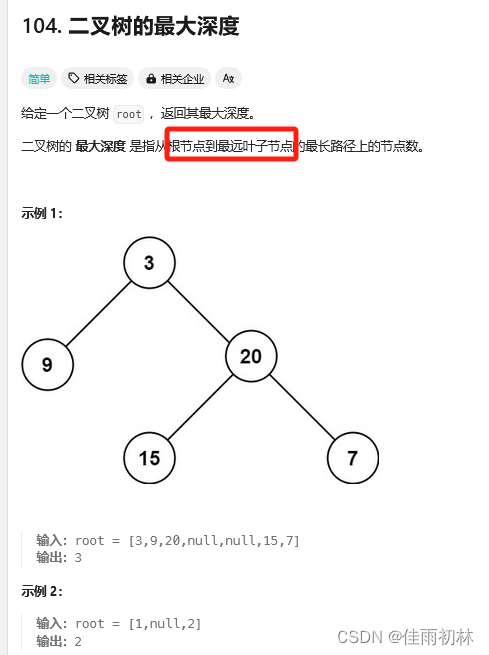
递归方法一：自己本身就是递归函数

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == NULL) return 0;
        int left_depth = maxDepth(root -> left);
        int right_depth = maxDepth(root -> right);
        //这里+1是指加上当前节点
        return max(left_depth, right_depth) + 1;
    }
};

递归方法二：自定义一个递归函数

class Solution {
public:
    int ans = 0;

    void function(TreeNode* node, int cnt){
        if(node == NULL){
            return;
        }           
        cnt += 1;
        ans = max(ans, cnt);
        function(node -> left, cnt);
        function(node -> right, cnt);
    }

    int maxDepth(TreeNode* root) {
        function(root, 0);
        return ans;
    }
};

1.2 二叉树的最小深度

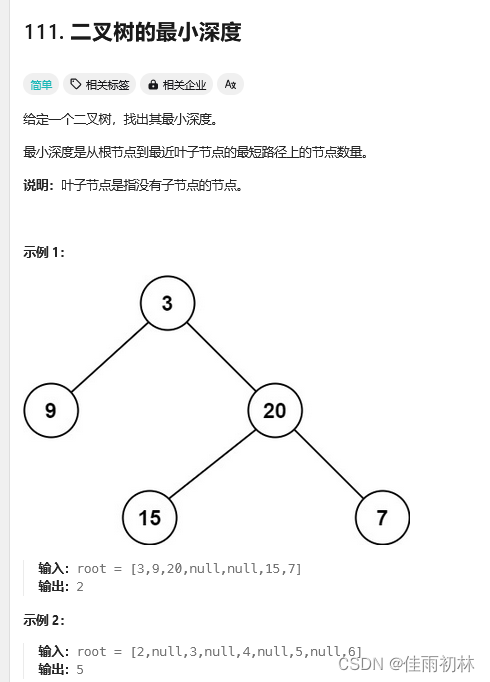
官方题解：

class Solution {
public:
    int minDepth(TreeNode *root) {
        if (root == nullptr) {
            return 0;
        }

        if (root->left == nullptr && root->right == nullptr) {
            return 1;
        }

        int min_depth = INT_MAX;
        if (root->left != nullptr) {
            min_depth = min(minDepth(root->left), min_depth);
        }
        if (root->right != nullptr) {
            min_depth = min(minDepth(root->right), min_depth);
        }

        return min_depth + 1;
    }
};

自己些的题解：

class Solution {
public:

    int minDepth(TreeNode* root) {
        if(root == NULL){
            return 0;
        }
        int left_depth = minDepth(root->left);
        int right_depth = minDepth(root -> right);
        if(left_depth == 0 || right_depth == 0){
        //题目路径的定义的是根节点到叶子节点,所出现左子树或者右子树为空的情况下，我们需要请用非空的子树部分
            return max(left_depth, right_depth) + 1;
        }else{
            return min(left_depth,right_depth) + 1;
        }
    }
};

1.3 路径总和

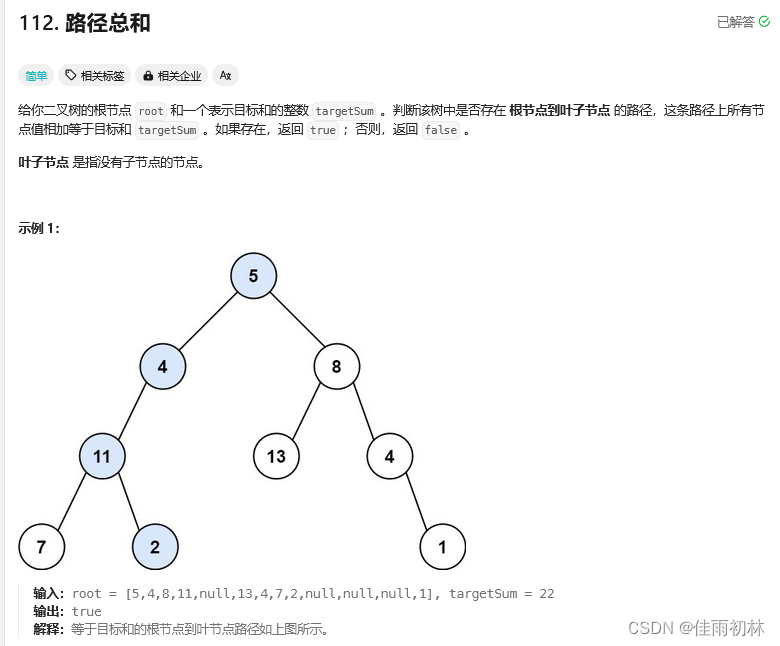
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == nullptr) return false;
        //表示到达了叶子节点，此时判断一下总和是否达到了targetSum
        if(root->right == nullptr && root->left == nullptr){
            return targetSum == root->val;
        }
        //每一次往下“递”时，减去当前节点的值
        return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root -> right, targetSum - root->val);
    }
};

1.4 路径总和II

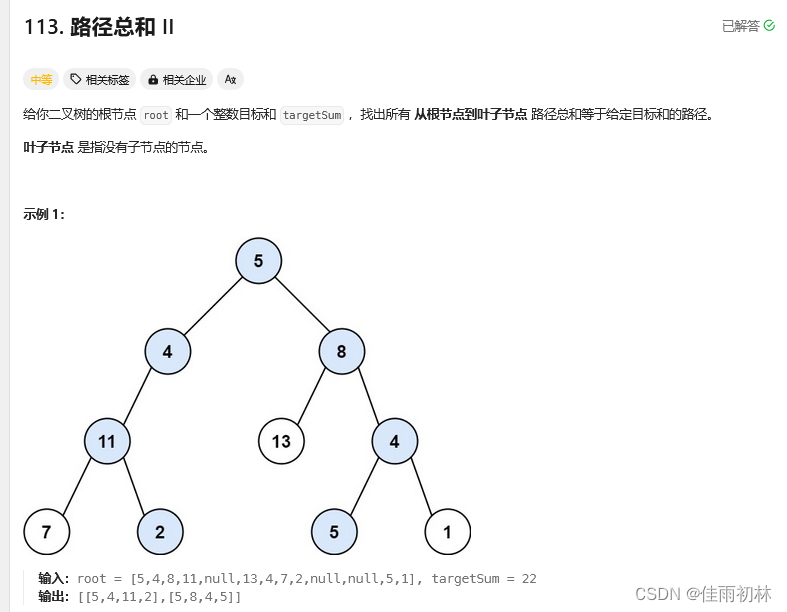
这个题目的难度相较于之前的题目难度大，实现过程中需要利用其他数据结构的帮助
java版题解：

class Solution {
    List<List<Integer>> ret = new LinkedList<List<Integer>>();
    Deque<Integer> path = new LinkedList<Integer>();

    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        dfs(root, targetSum);
        return ret;
    }

    public void dfs(TreeNode root, int targetSum){
        if(root == null){
            return;
        }
        path.offerLast(root.val);
        targetSum -= root.val;
        if(root.left == null && root.right == null && targetSum == 0){
            ret.add(new LinkedList<Integer>(path));
        }
        dfs(root.left, targetSum);
        dfs(root.right, targetSum);
        path.pollLast();
    }
}

C++版本题解：

class Solution {
public:
    vector<vector<int>> ret;
    vector<int> path;

    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        dfs(root, targetSum);
        return ret;
    }

    void dfs(TreeNode* root, int targetSum){
        if(root == nullptr){
            return;
        }
        //尝试性地将当前值添加到路径中
        path.push_back(root->val);
        //减去加入的值
        targetSum -= root->val;
        //当前节点为叶子节点同时满足总和要求
        if(root->left == nullptr && root->right == nullptr && targetSum == 0){
            ret.push_back(path);
        }
        //继续遍历左子树
        dfs(root->left, targetSum);
        //继续遍历右子树
        dfs(root->right, targetSum);
        //将尝试性加入的节点值弹出来
        path.pop_back();
    }
};

1.5 根节点到叶子节点数字之和

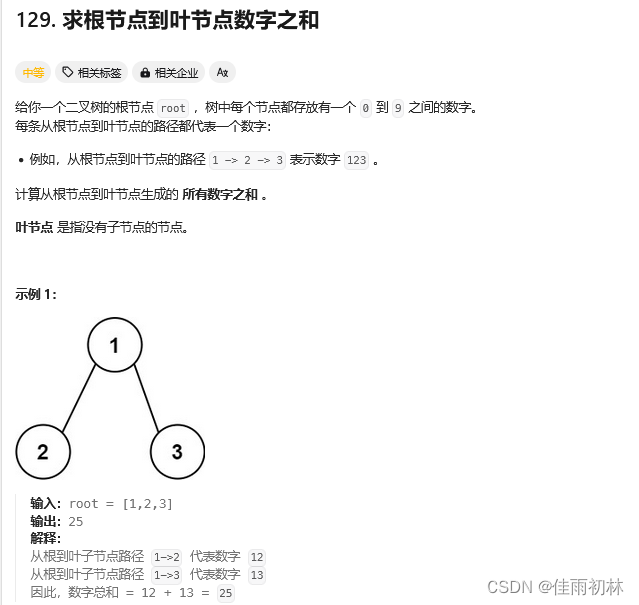
//java题解
class Solution {
    int sum = 0;
    public int sumNumbers(TreeNode root) {
        dfs(root, 0);
        return sum;
    }
    void dfs(TreeNode root, int cnt){
        if(root == null) return;
        cnt = cnt * 10 + root.val;
        //到达了根节点，加入到总和中
        if(root.left == null && root.right == null){
            sum += cnt;
        }
        //遍历左子树和右子树
        dfs(root.left, cnt);
        dfs(root.right, cnt);
    }
}

1.6 二叉树的所有路径

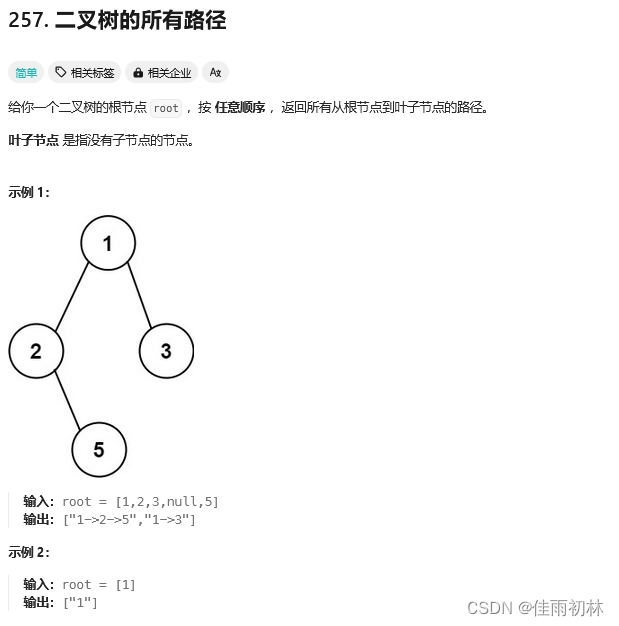自己写的解法（StringBuffer处的来回处理过于冗杂）

class Solution {
    List<String> ans = new LinkedList<>();
    StringBuffer sb = new StringBuffer();

    public List<String> binaryTreePaths(TreeNode root) {
        dfs(root);
        return ans;
    }

    void dfs(TreeNode root){
        if(root == null) return;
        sb.append(root.val + "");
        sb.append("->");
        if(root.left == null && root.right == null){
            ans.add(sb.substring(0, sb.length()-2));
        }
        dfs(root.left);
        dfs(root.right);
        sb.delete(sb.length() - 2 - (root.val + "").length(), sb.length());
    }
}

参考题解：

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> paths = new ArrayList<String>();
        constructPaths(root,"", paths);
        return paths;
    }
    public void constructPaths(TreeNode root, String path, List<String> paths){
        if(root != null){
            StringBuffer pathSB = new StringBuffer(path);
            pathSB.append(Integer.toString(root.val));
            if(root.left == null && root.right == null){//在当前节点时叶子节点
                paths.add(pathSB.toString());
            }else{
                pathSB.append("->");
                constructPaths(root.left, pathSB.toString(),paths);
                constructPaths(root.right, pathSB.toString(), paths);
            }
        }
    }
}

1.7 统计二叉树中好节点的数目

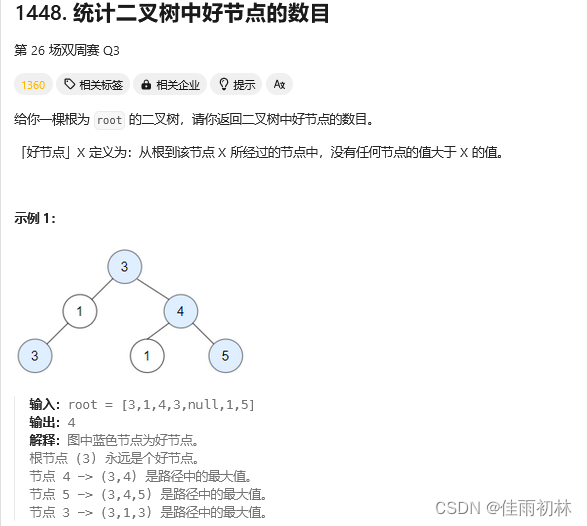
自己写的题解，通过定义全局变量实现题目解答：

class Solution {
    int ans  = 0;
    public int goodNodes(TreeNode root) {
        dfs(root, -10001);
        return ans;
    }

    void dfs(TreeNode root, int max){
        if(root == null){
            return;
        }
        if(root.val >= max){
            ans++;
            max = root.val;
        }
        dfs(root.left, max);
        dfs(root.right, max);
    }
}

参考题解，无需定义全局变量版本：

class Solution {
    public int goodNodes(TreeNode root) {
        return dfs(root, Integer.MIN_VALUE);
    }

    int dfs(TreeNode root, int mx){
        if(root == null){
            return 0;
        }
        int left = dfs(root.left,Math.max(mx, root.val));
        int right = dfs(root.right, Math.max(mx, root.val));
        return left + right + (mx <= root.val ? 1 : 0);
    }
}