洛谷 P4005 小Y和地铁

样例解释

---

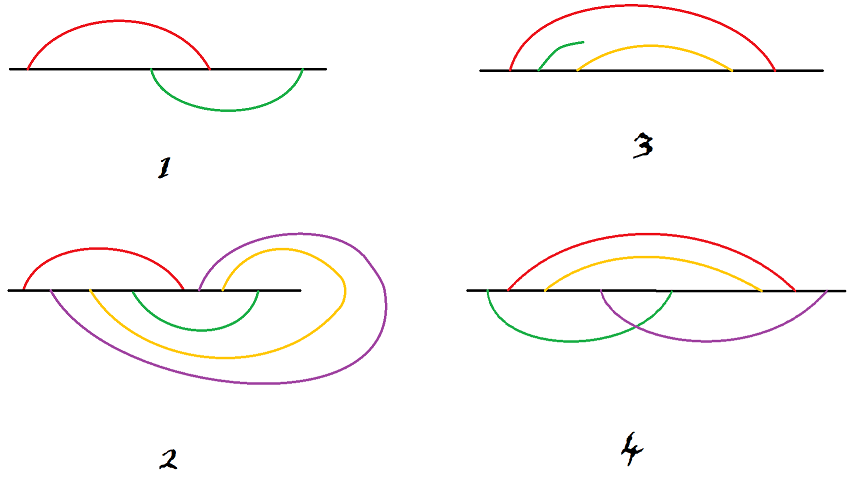
简单的想法

只和0号线有1个交点的线路可以不用考虑，因为可以把它的长度看做无限短。

如果有一条线路左右端点间没有另外一条线的端点，那么这条线可以直接删除。这样操作至没有可以删除的线为止。

这样子样例3就可以不用考虑任何的线路直接输出0了……

---

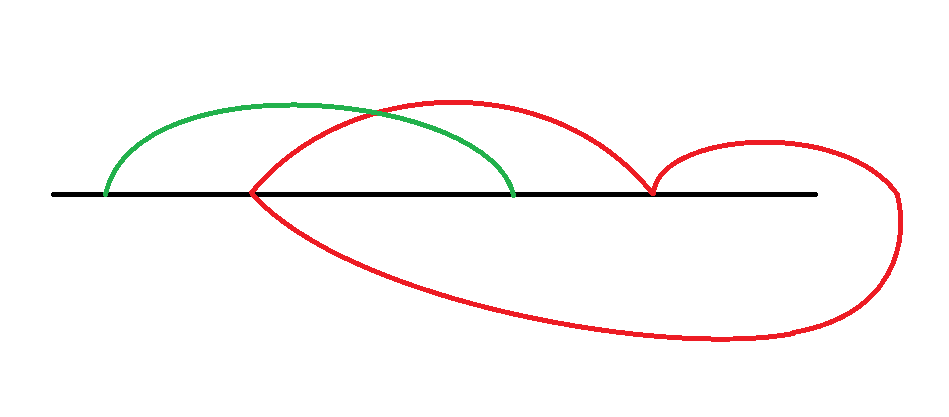
一条线和0号线的位置关系

dfs。

枚举每条线和0号线的位置关系+暴力找交点。

时间复杂度O(?·8^(?/2))，大概只能得10分左右

---

考虑优化状态数——

可以看出，另一条线要么不经过这两条线，要么同时经过这两条线。

状态由8种变为4种

复杂度O(?·4^(?/2))，大概可以得 16分左右

---

再来考虑优化状态数——

这个似乎并不能满足其它的线同时经过，或同时不经过这两条线啊？

对于每条线的左端点从小到大排序，且在dfs中从小到大的考虑每一条线。

所以只用考虑左端点在当前线后面的线，不会出现上述情况。

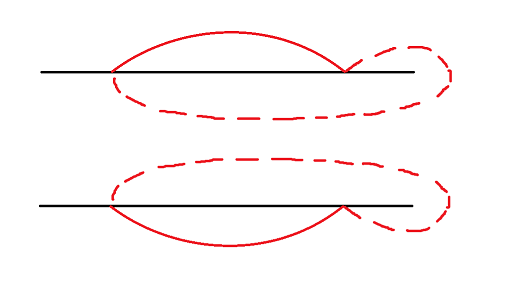
现在可以看做只有两种状态了。

每种状态的虚线、实线两种情况 可以贪心的选择一种和前面的线交点最少的。

复杂度O(?·2^(?/2))，人品好的话可以得90分？

---

优化找交点

考虑加入一条线会对一段区间造成影响，即后面有端点含于这段区间的线有可能会与这条线相交，可以尝试使用可以维护区间操作的数据结构优化。

使用树状数组优化！

每加入一条线，就把它覆盖的区间值+1。更新交点数时只需要加上它的左右端点上的值之差就可以了。

复杂度 O(2^(?/2) ???2^?)，注意下常数就可以过了

---

代码

#include<bits/stdc++.h>
using namespace std;

#define maxn 44
#define read(x) scanf("%d",&x)

#define lowbit(x) (x&-x)

#define query(x,y,L,R) min(qryx(x,y,L,R),qryy(x,y,L,R))
#define qryx(x,y,L,R) (x.Query(R)-x.Query(L-1))
#define qryy(x,y,L,R) (x.Query(n)-x.Query(R-1)+y.Query(n)-y.Query(L-1))

int n;
int a[maxn+5];
int ans;

struct Pair{
	int x,y;
	Pair(){}
	Pair(int xx,int yy) {
		x=xx,y=yy;
	}
	bool operator < (const Pair& oth) const {
		return x<oth.x||(x==oth.x&&y<oth.y);
	}
};

vector<Pair> vec;

struct bst{
	int sum[maxn+5];
	bst(){}
	void add(int x,int d) {
		while(x<=n) {sum[x]+=d,x+=lowbit(x);}
	}
	int Query(int x) {
		int s=0;
		while(x>0) {s+=sum[x],x-=lowbit(x);}
		return s;
	}
};

bst bstup,bstdown;

void init() {
	n=0,ans=1e9,vec.clear();
	memset(bstup.sum,0,sizeof(bstup.sum));
	memset(bstdown.sum,0,sizeof(bstdown.sum));
}

void readin() {
	int nn;
	read(nn);
	
	int x[maxn+5];
	map<int,int> mp;
	for(int i=1;i<=nn;i++) {
		read(x[i]);
		if(mp.count(x[i])) mp[x[i]]++;
		else mp[x[i]]=1;
	}
	
	int use[maxn+5]={0},cnt=0;
	for(int i=1;i<=nn;i++) {
		if(mp[x[i]]<=1) continue;
		if(use[x[i]]&&use[x[i]]==a[n]) {n--;continue;}
		a[++n]=use[x[i]]?use[x[i]]:(use[x[i]]=++cnt);
	}
	
	for(int i=1;i<=n;i++) {
		for(int j=i+1;j<=n;j++) {
			if(a[i]==a[j]) vec.push_back(Pair(i,j));
		}
	}
	sort(vec.begin(),vec.end());
}

void dfs(int x,int s) {
	if(x==vec.size()) {
		ans=min(ans,s);
		return ;
	}
	if(s>=ans) return ;
	int s1=query(bstup,bstdown,vec[x].x,vec[x].y);
	bstup.add(vec[x].y,1);
	dfs(x+1,s+s1);
	bstup.add(vec[x].y,-1);
	
	int s2=query(bstdown,bstup,vec[x].x,vec[x].y);
	bstdown.add(vec[x].y,1);
	dfs(x+1,s+s2);
	bstdown.add(vec[x].y,-1);
}

int main() {
	int T;
	read(T);
	while(T--) {
		init();
		readin();
		dfs(0,0);
		printf("%d\n",ans);
	}
	return 0;
}