水流问题（Dfs

卡码网 补充C#版

103. 水流问题

题目描述

现有一个 N × M 的矩阵，每个单元格包含一个数值，这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界，而矩阵的右边界和下边界被视为第二组边界。

矩阵模拟了一个地形，当雨水落在上面时，水会根据地形的倾斜向低处流动，但只能从较高或等高的地点流向较低或等高并且相邻（上下左右方向）的地点。我们的目标是确定那些单元格，从这些单元格出发的水可以达到第一组边界和第二组边界。

输入描述

第一行包含两个整数 N 和 M，分别表示矩阵的行数和列数。 

后续 N 行，每行包含 M 个整数，表示矩阵中的每个单元格的高度。

输出描述

输出共有多行，每行输出两个整数，用一个空格隔开，表示可达第一组边界和第二组边界的单元格的坐标，输出顺序任意。

输入示例

5 5
1 3 1 2 4
1 2 1 3 2
2 4 7 2 1
4 5 6 1 1
1 4 1 2 1

输出示例

0 4
1 3
2 2
3 0
3 1
3 2
4 0
4 1

提示信息

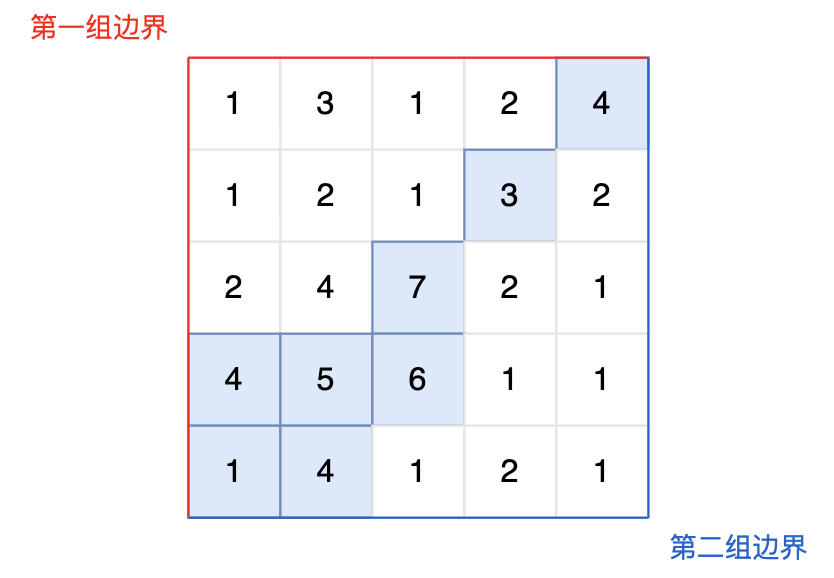
图中的蓝色方块上的雨水既能流向第一组边界，也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。 

数据范围：

1 <= M, N <= 100。

 思路：主要就是分别从四个边开始遍历一遍边 然后外部设置的bool类型的两个相同大小数组 当符合条件（下一个位置值大于自己现在的位置值）就标注为true ，在分别遍历之后 寻找两个数组中公共为true的部分 就是可以从这个点到一组和另一组的水流起始点  

using System;

class Program
{
    public static int n;
    public static int m;
    static void Main()
    {
        string[] inputs=Console.ReadLine().Split();       
         n=int.Parse(inputs[0]);
         m=int.Parse(inputs[1]);
        
        // 声明数组 填充输入数组
        int[,] grid=new int [n,m];
        for(int i=0;i<n;i++)
        {
            inputs=Console.ReadLine().Split();
            for(int j=0;j<m;j++)
            {
                grid[i,j]=int.Parse(inputs[j]);
            }
        }
       // CountIsLand(grid,n,m);
        // 申明两个和图大小一致的大小和规格的bool类型数组
        bool[,] board1=new bool[m,n]; //装载第一组边界的判定值 左上 
        bool[,] board2=new bool[m,n];//第二组边界判定值  右下
        //从左右边界进行dfs
        for(int i=0;i<n;i++)
        {
            Dfs(grid,i,0,board1,int.MinValue);//遍历最左列
            Dfs(grid ,i,m-1,board2,int.MinValue);
        }
        //对上下边界进行dfs
        for(int j=0;i<m;j++)
        {
            Dfs(grid,0,j,board1,int,MinValue);
            Dfs(grid,n-1,j,board2,int.MinValue);
        }
        //打印结果
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                if(board1[i,j]&&board2[i,j]) //如果两个真假图中同一位置都是真 代表此点能达到两个边界
                {
                    Console.WriteLine(i+" "+j);
                    Console.WriteLine();
                }
            }
        }
        
    }
    public static void Dfs(int[,] grid ,int r,int c,bool[,] board,int pre)
    {
        if(r<0 ||r >=n ||c<0||c>=m)
        {
            return ;
        }
        if(grid[r,c]<pre) //如果遍历到的下一个值小于pre也就是当前值 那么证明没法走通这个格子直接返回
        {
            return ;
        }
        board[r,c]=true;
        
        Dfs(grid,r,c+1,board,grid[r,c]);
        Dfs(grid,r,c-1,board,grid[r,c]);
        Dfs(grid,r+1,c,board,grid[r,c]);
        Dfs(grid,r-1,c,board,grid[r,c]);
    }
}