岛屿的周长 （Dfs法与 普通if判断法

卡码网    只给了普通解法  去力扣学习发现两种解法  一种是Dfs

另一种是纯粹的遍历每个格子的上下左右判断是不是超出边界或者是海水 是的话就 让边数加加

106. 岛屿的周长

题目描述

给定一个由 1（陆地）和 0（水）组成的矩阵，岛屿是被水包围，并且通过水平方向或垂直方向上相邻的陆地连接而成的。

你可以假设矩阵外均被水包围。在矩阵中恰好拥有一个岛屿，假设组成岛屿的陆地边长都为 1，请计算岛屿的周长。岛屿内部没有水域。

输入描述

第一行包含两个整数 N, M，表示矩阵的行数和列数。之后 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。

输出描述

输出一个整数，表示岛屿的周长。

输入示例

5 5
0 0 0 0 0 
0 1 0 1 0
0 1 1 1 0
0 1 1 1 0
0 0 0 0 0

输出示例

14

提示信息

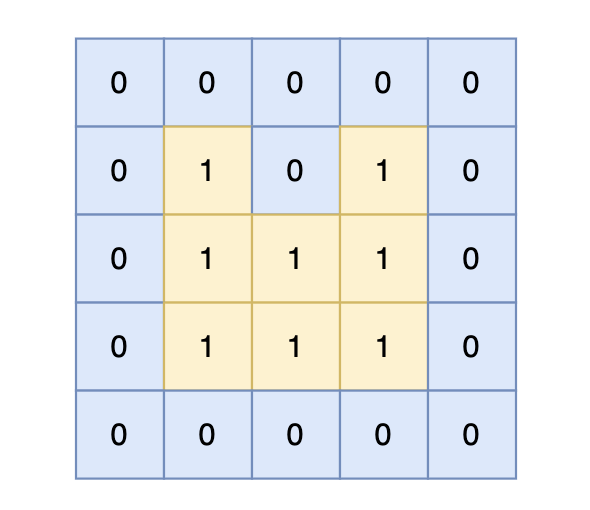
岛屿的周长为 14。

数据范围：

1 <= M, N <= 50。

 解法一 普通判断解法

using System;

class Program
{
    static void Main()
    {
        //读取输入
        string[] firstLine=Console.ReadLine().Split();//读取一行输入并将其分割成一个字符串数组
        int n=int.Parse(firstLine[0]);
        int m=int.Parse(firstLine[1]);
        //总边数
        int result=0;
        //填充岛屿
        int[,] grid=new int[n,m];
        
        for(int i=0;i<n;i++)
        {
            firstLine=Console.ReadLine().Split();
            for(int j=0;j<m;j++)     //填充每一行
            {
                grid[i,j]=int.Parse(firstLine[j]);
            }
        }
        
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                if(grid[i,j]==1)
                {
                    if(i-1<0 || grid[i-1,j]==0) //如果此位置的上方超出边界 或者 为0 那么让边加一
                    {
                        result++;
                    }
                    if(i+1>=n || grid[i+1,j]==0)//如果此位置的下方超出边界 或者 为0 那么让边加一
                    {
                        result++;
                    }
                    if(j-1<0 ||grid [i,j-1]==0)//如果此位置的左方超出边界 或者 为0 那么让边加一
                    {
                        result++;
                    }
                    if(j+1>=m ||grid [i,j+1]==0)//如果此位置的右方超出边界 或者 为0 那么让边加一
                    {
                        result++;
                    }
                }
            }
        }
        Console.WriteLine(result);
        
    }
    
}

解法二 DFs Dfs法 要在返回值做文章  ，dfs 函数直接返回有这几种情况：

!inArea(grid, r, c)，即坐标 (r, c) 超出了网格的范围，此情况证明该网格挨着一个图的边 对应边加一

grid[r][c] != 1，即当前格子不是岛屿格子，这又分为两种情况：1.grid[r][c] == 0，当前格子是海洋格子 对应边加一         2.grid[r][c] == 2，当前格子是已遍历的陆地格子 没有用 直接返回0

using System;

class Program
{
    static void Main()
    {
        //读取输入
        string[] firstLine=Console.ReadLine().Split();//读取一行输入并将其分割成一个字符串数组
        int n=int.Parse(firstLine[0]);
        int m=int.Parse(firstLine[1]);
        //总边数
        int result=0;
        //填充岛屿
        int[,] grid=new int[n,m];
        
        for(int i=0;i<n;i++)
        {
            firstLine=Console.ReadLine().Split();
            for(int j=0;j<m;j++)     //填充每一行
            {
                grid[i,j]=int.Parse(firstLine[j]);
            }
        }
        
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                if(grid[i,j]==1)
                {
                    result=Dfs(grid,i,j);
                }
            }
        }
        Console.WriteLine(result);
        
    }
    public int Dfs(int[,] grid ,int r,int c)
    {
        if(r<0 || r>=n || c<0 ||c>=m) //检测到出边界了 证明这个位置和边界相连返回1 
        {
            return 1;
        }
        if(grid[r,c]==0) //检测到当前位置是海洋位置 给前一个遍历到这个位置的陆地值加1 
        {
            return 1;
        }
        if(grid[r,c] ==2) //检测到已经便利过的地方 不做操作 
        {
            return 0;
        }
        grid[r,c]=2;
        return Dfs(grid,r+1,c)+Dfs(grid,r-1,c)+Dfs(grid,r,c+1)+Dfs(grid,r,c-1);

    }
}