医学图像分割评价指标Dice与HD95的详解

原创已于 2025-11-05 22:07:26 修改 · 1.1k 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #医学影像 #语义分割

于 2025-11-05 18:58:41 首次发布

Dice

关于dice就不再多赘述，作者的另外一篇文章里提及：

https://blog.youkuaiyun.com/qq_73038863/article/details/152008677?fromshare=blogdetail&sharetype=blogdetail&sharerId=152008677&sharerefer=PC&sharesource=qq_73038863&sharefrom=from_link

HD95

定义

豪斯多夫距离（Hausdorff Distance, HD）衡量两个点集之间的最大边界偏差。但在医学图像中，由于噪声或标注误差，最大距离容易受离群点影响，因此常用 95% 分位数的 HD（HD95）作为更鲁棒的替代。

计算步骤

提取预测结果和真实标签的边界点集（如使用 scipy.ndimage 或 skimage.segmentation.find_boundaries）。

对每个预测边界点，计算其到所有真实边界点的最小欧氏距离。同样，对每个真实边界点，计算其到预测边界的最小距离。合并所有距离，取 95% 分位数作为 HD95。

特点

（1）物理单位（如毫米，若图像有空间分辨率信息）或像素。

（2）对边界精度高度敏感，能反映分割轮廓的几何准确性。

（3）值越小越好，理想值为 0（边界完全重合）。

接下来对dice与hd95在实际中的计算代码讲解一下，下面的代码是transunet网络结构中的utils.py代码：

import numpy as np
import torch
from medpy import metric
from scipy.ndimage import zoom
import torch.nn as nn
import SimpleITK as sitk


# -------------------- Dice Loss --------------------
class DiceLoss(nn.Module):
    def __init__(self, n_classes):
        super(DiceLoss, self).__init__()
        self.n_classes = n_classes

    def _one_hot_encoder(self, input_tensor):
        tensor_list = []
        for i in range(self.n_classes):
            temp_prob = input_tensor == i
            tensor_list.append(temp_prob.unsqueeze(1))
        output_tensor = torch.cat(tensor_list, dim=1)
        return output_tensor.float()

    def _dice_loss(self, score, target):
        target = target.float()
        smooth = 1e-5
        intersect = torch.sum(score * target)
        y_sum = torch.sum(target * target)
        z_sum = torch.sum(score * score)
        loss = (2 * intersect + smooth) / (z_sum + y_sum + smooth)
        return 1 - loss

    def forward(self, inputs, target, weight=None, softmax=False):
        if softmax:
            inputs = torch.softmax(inputs, dim=1)
        target = self._one_hot_encoder(target)
        if weight is None:
            weight = [1] * self.n_classes
        assert inputs.size() == target.size(), \
            f'predict {inputs.size()} & target {target.size()} shape do not match'
        loss = 0.0
        for i in range(self.n_classes):
            dice = self._dice_loss(inputs[:, i], target[:, i])
            loss += dice * weight[i]
        return loss / self.n_classes


# -------------------- Metric Computation --------------------
def calculate_metric_percase(pred, gt, spacing_z=2.5):
    """
    Compute Dice and 95% Hausdorff Distance (HD95) for a single organ.
    
    Args:
        pred (np.ndarray): Predicted binary mask, shape (D, H, W)
        gt (np.ndarray): Ground truth binary mask, shape (D, H, W)
        spacing_z (float): Spacing in z-direction (slice thickness) in mm.
                           x/y spacing is assumed to be 1.0 mm (common simplification).
    
    Returns:
        dice (float): Dice Similarity Coefficient [0, 1]
        hd95 (float): 95% Hausdorff Distance in mm
    """
    pred = (pred > 0).astype(np.bool_)
    gt = (gt > 0).astype(np.bool_)

    if pred.sum() == 0 and gt.sum() == 0:
        # Both empty → perfect match
        return 1.0, 0.0
    elif pred.sum() == 0 or gt.sum() == 0:
        # One empty, the other not → worst case
        return 0.0, 100.0  # HD95 capped at 100 mm (common practice)
    else:
        dice = metric.binary.dc(pred, gt)
        # medpy expects voxelspacing in the same order as array dimensions: (z, y, x)
        hd95 = metric.binary.hd95(pred, gt, voxelspacing=(spacing_z, 1.0, 1.0))
        return dice, hd95


# -------------------- Inference on One Volume --------------------
def test_single_volume(image, label, net, classes, patch_size=[256, 256],
                       test_save_path=None, case=None, z_spacing=2.5):
    """
    Test on a single 3D volume.
    
    Args:
        image (torch.Tensor): Input image, shape (1, D, H, W)
        label (torch.Tensor): Ground truth label, shape (1, D, H, W)
        net (nn.Module): Segmentation model
        classes (int): Number of classes (including background)
        patch_size (list): Patch size for 2D inference [H, W]
        test_save_path (str): Path to save predictions (optional)
        case (str): Case name for saving
        z_spacing (float): Slice thickness in mm
    
    Returns:
        metric_list (list): List of (dice, hd95) for classes 1 to classes-1
    """
    image = image.squeeze(0).cpu().detach().numpy()  # (D, H, W)
    label = label.squeeze(0).cpu().detach().numpy()  # (D, H, W)

    if len(image.shape) == 3:
        prediction = np.zeros_like(label, dtype=np.uint8)
        for ind in range(image.shape[0]):  # iterate over slices (z-axis)
            slice = image[ind, :, :]  # (H, W)
            x, y = slice.shape
            # Resize to patch_size if needed
            if x != patch_size[0] or y != patch_size[1]:
                slice = zoom(slice, (patch_size[0] / x, patch_size[1] / y), order=3)
            input_tensor = torch.from_numpy(slice).unsqueeze(0).unsqueeze(0).float().cuda()

            net.eval()
            with torch.no_grad():
                outputs = net(input_tensor)
                out = torch.argmax(torch.softmax(outputs, dim=1), dim=1).squeeze(0)
                out = out.cpu().detach().numpy()

            # Resize back to original slice size
            if x != patch_size[0] or y != patch_size[1]:
                pred = zoom(out, (x / patch_size[0], y / patch_size[1]), order=0)
            else:
                pred = out
            prediction[ind] = pred.astype(np.uint8)
    else:
        # 2D case (unlikely for Synapse)
        input_tensor = torch.from_numpy(image).unsqueeze(0).unsqueeze(0).float().cuda()
        net.eval()
        with torch.no_grad():
            out = torch.argmax(torch.softmax(net(input_tensor), dim=1), dim=1).squeeze(0)
            prediction = out.cpu().detach().numpy().astype(np.uint8)

    # Compute metrics for each class (skip class 0: background)
    metric_list = []
    for i in range(1, classes):
        dice, hd95 = calculate_metric_percase(
            pred=(prediction == i),
            gt=(label == i),
            spacing_z=z_spacing
        )
        metric_list.append((dice, hd95))

    # Optional: Save results as NIfTI
    if test_save_path is not None:
        img_itk = sitk.GetImageFromArray(image.astype(np.float32))
        prd_itk = sitk.GetImageFromArray(prediction.astype(np.uint8))
        lab_itk = sitk.GetImageFromArray(label.astype(np.uint8))
        # Set spacing: (x, y, z) for SimpleITK
        img_itk.SetSpacing((1.0, 1.0, z_spacing))
        prd_itk.SetSpacing((1.0, 1.0, z_spacing))
        lab_itk.SetSpacing((1.0, 1.0, z_spacing))
        sitk.WriteImage(prd_itk, f'{test_save_path}/{case}_pred.nii.gz')
        sitk.WriteImage(img_itk, f'{test_save_path}/{case}_img.nii.gz')
        sitk.WriteImage(lab_itk, f'{test_save_path}/{case}_gt.nii.gz')

    return metric_list

结构如下：

训练阶段：
    model → DiceLoss（Part 1） → loss → backward()

测试阶段：
    test_single_volume（Part 3）
        │
        ├─ 逐 slice 推理（模型前向）
        │
        └─ 对每个器官调用 calculate_metric_percase（Part 2）
               │
               ├─ 计算 Dice（用 medpy）
               └─ 计算 HD95（用 medpy + spacing）

注：Dice 损失（Dice Loss）和 Dice 系数（Dice Coefficient / Dice Score）密切相关，但本质不同，它们的关系可以概括为：Dice 损失 = 1 − Dice 系数

用途不同

Dice 系数：是一个评价指标（metric），用于衡量模型分割结果与真值的重叠程度。
→ 用在 test_single_volume 中，报告“模型表现好不好”。

Dice 损失：是一个损失函数（loss function），用于指导模型训练。
→ 用在 train.py 中，告诉模型“往哪个方向更新参数”。

输入形式不同

Dice 系数（评估时）：

输入必须是二值化的硬分割结果（如 pred = (output > 0.5) 或 argmax 后的整数图）。

Dice 损失（训练时）：

输入是连续的概率值（通常经过 softmax/sigmoid），保留梯度信息。

代码讲解

utils.py 中，Dice 和 HD95 的计算发生在测试阶段，由以下两个函数协作完成：

（1）test_single_volume：对一个 3D 医学图像（如 CT）进行 slice-by-slice 推理，生成完整 3D 预测。

（2）calculate_metric_percase：对每个器官类别（如肝脏、脾脏）分别计算 Dice 和 HD95。

calculate_metric_percase

给定一个器官的 3D 预测和真值，安全、准确地计算出它在“区域重叠”（Dice）和“边界精度”（HD95，单位 mm）上的表现。

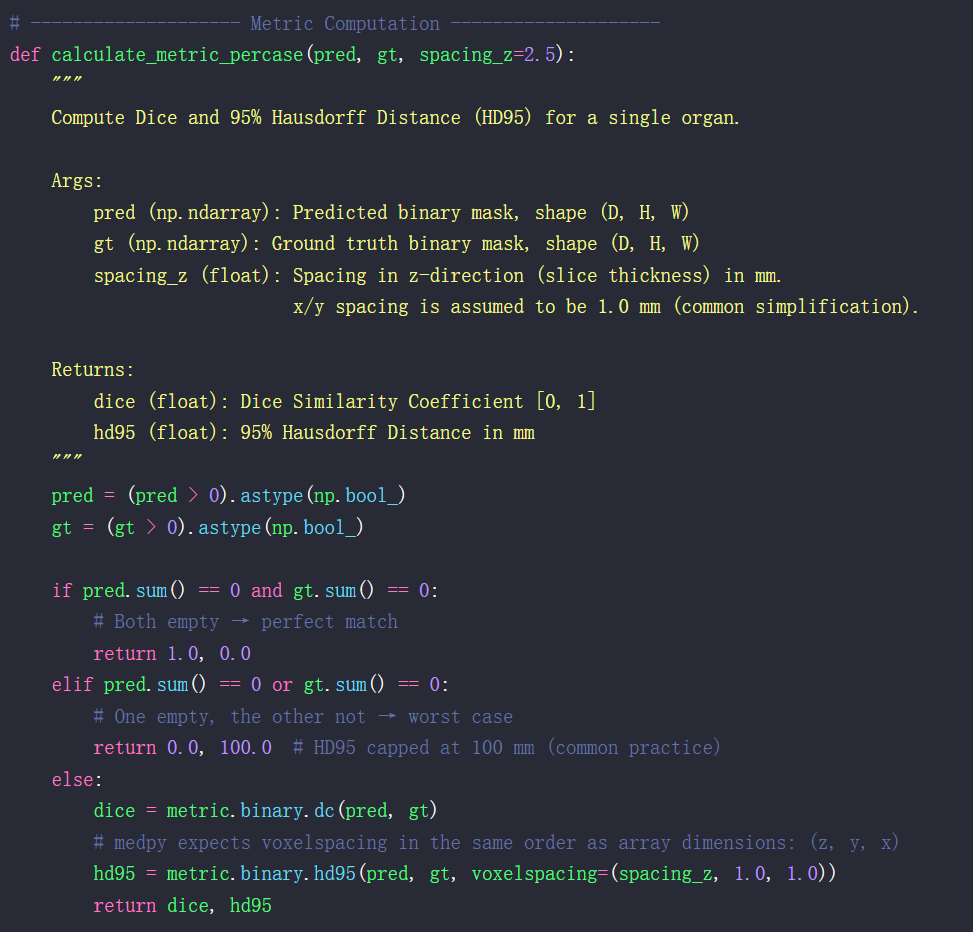
第 1 步：二值化处理

pred = (pred > 0).astype(np.bool_)
gt = (gt > 0).astype(np.bool_)

确保输入是布尔型（True/False），这是 medpy 的要求。即使输入是整数标签（如 0/1），也显式转为 bool。

第 2 步：处理极端情况（避免崩溃）

if pred.sum() == 0 and gt.sum() == 0:
    return 1.0, 0.0          # 都没这个器官 → 完美
elif pred.sum() == 0 or gt.sum() == 0:
    return 0.0, 100.0        # 一个有，一个没有 → 最差

如果不做这个判断，当预测或真值全为 0 时，medpy 会报错或返回无效值（如 inf）。这是医学图像中常见情况（某些器官可能缺失或未标注）。

第 3 步：计算 Dice 系数

dice = metric.binary.dc(pred, gt)

第 4 步：计算 HD95（边界精度）

hd95 = metric.binary.hd95(pred, gt, voxelspacing=(spacing_z, 1.0, 1.0))

参数：

pred：模型预测的该器官的 3D 二值掩码（shape: (D, H, W)，值为 True/False 或 0/1）

gt：医生标注的该器官的 3D 真实掩码（同样 shape 和类型）

spacing_z：CT/MRI 切片在 z 轴（层厚）的物理间距，单位 mm（例如 2.5 mm）

voxelspacing：

medpy 要求 voxelspacing 的顺序与数组维度一致。如果 pred 和 gt 是 (D, H, W)，对应：

D → z 轴（切片方向）

H → y 轴

W → x 轴

所以 voxelspacing=(z_spacing, y_spacing, x_spacing) = (spacing_z, 1.0, 1.0)

为什么 x 与 y 是 1.0？
在很多公开数据集（如 Synapse multi-organ CT）中，原始图像的 x/y 分辨率接近 1mm，而 z 间距变化较大（如 2.5mm、5mm）。为简化，常假设 x/y=1.0，只校正 z 方向。

内部原理（由 `medpy` 实现）

medpy.metric.binary.hd95 内部执行以下操作：

提取前景点坐标：

pred_points = np.argwhere(pred)  # shape: (N, 3)
gt_points = np.argwhere(gt)      # shape: (M, 3)

将像素坐标转换为物理坐标（mm）：

pred_points_mm = pred_points * np.array([spacing_z, 1.0, 1.0])
gt_points_mm = gt_points * np.array([spacing_z, 1.0, 1.0])

计算双向最近距离：

对每个 pred_point，找最近的 gt_point → 得到 N 个距离

对每个 gt_point，找最近的 pred_point → 得到 M 个距离

合并所有距离，取 95% 分位数：

all_distances = np.concatenate([dist_pred_to_gt, dist_gt_to_pred])
hd95 = np.percentile(all_distances, 95)

medpy.metric.binary.hd95 内部操作可能不好理解，下面是通俗理解的例子，可以试着看一下。

概念	通俗理解
图像数组 (D, H, W)	一本 CT 相册：D 页，每页 H 行 W 列
voxelspacing	告诉你：翻一页走多远（z），一行=几毫米（y），一列=几毫米（x）
坐标转换	把“第几页第几行第几列” → 换算成“多少毫米”的真实位置
HD95 计算	看预测和真实的器官边界，95% 的地方最大差多少毫米
为什么用 95%	防止一个“手抖画错”的点毁掉整个评分