BN（Batch Normalization）层的作用

注：作者为初学者，有些知识不太熟悉，可能描述有误，望见谅。

BN层概念

        BN，全称Batch Normalization（批量归一化），由Ioffe和Szegedy在2015年提出，是深度学习中用于加速训练、提升模型稳定性的技术。其核心思想是对神经网络每一层的输入进行标准化处理（均值为0、方差为1），并通过可学习的参数（缩放因子γ和偏移因子β）保留模型的表达能力。

BN层作用

缓解内部协变量偏移：减少网络层输入分布随训练发生剧烈变化的问题，使每一层的输入分布更稳定。

加速训练收敛：允许使用更大的学习率，减少对参数初始化的依赖。

轻微正则化效果：通过每个批次的均值和方差计算引入噪声（在训练时使用批次统计量，如均值和方差，而测试时使用全局统计量。这种差异本身可视为一种噪声来源），类似Dropout的效果。

引入噪声的原因以及作用：

提升模型泛化能力
        噪声的引入可以防止模型对训练数据中的特定模式或特征产生过度依赖，从而减少过拟合。类似于Dropout通过随机屏蔽神经元迫使网络学习更鲁棒的特征，噪声的加入也能让模型对输入数据的小扰动更具鲁棒性。

模拟数据增强效果
        噪声可以视为隐式的数据增强，即使输入数据未显式扩充，噪声也能在特征层面生成变体。这有助于模型学习更全面的数据分布，而非依赖训练集中的偶然性模式。

改善优化过程
        噪声可能打破训练中的局部最优或平坦区域，使优化路径更具探索性。例如，在Batch Normalization中，随机噪声可能缓解梯度消失或爆炸问题，加速收敛。

实现模型集成效应
        类似Dropout的噪声在训练时生成多个子模型，测试时通过平均效果近似集成学习。这种“隐式集成”能提升预测稳定性，尤其在数据量有限时。

BN层原理

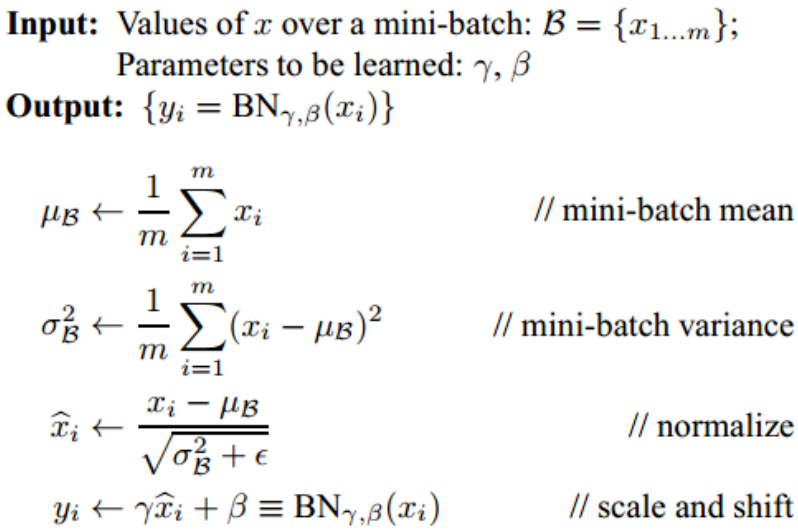
（1）取一个 mini-batch，设当前层净输入矩阵Z = [z₁, z₂, …, zₘ]ᵀ  ，形状 (m, d)，m = batch_size，d = 特征维度（CNN 里即“通道数”）。
（2）计算批统计量（逐维度）。对每一维 j (j = 1…d)：批均值μⱼ = 1/m · Σᵢ zᵢⱼ，批方差σⱼ² = 1/m · Σᵢ (zᵢⱼ − μⱼ)² + ε(ε 防止除零，≈1e-5)。
（3）标准化（逐维度）。得到零均值、单位方差中间结果ẑᵢⱼ = (zᵢⱼ − μⱼ) / √(σⱼ²)。
（4）可学习缩放与平移。引入可训练参数γⱼ：缩放因子（初始 1），βⱼ：平移因子（初始 0）。输出yᵢⱼ = γⱼ · ẑᵢⱼ + βⱼ。让网络自行决定“是否且如何”把分布再挪回最有表达力的位置。

BN层使用位置

        通常是“线性”后，激活函数前使用BN层。代码示例:

import torch.nn as nn

model = nn.Sequential(
    nn.Linear(100, 50),
    nn.BatchNorm1d(50),  # 全连接层后的BN
    nn.ReLU(),
    nn.Conv2d(3, 64, kernel_size=3),
    nn.BatchNorm2d(64),  # 卷积层后的BN
    nn.LeakyReLU()
)
 

注：使用BN层后，训练循环里先写 model.train()，在测试/推理循环里先写 model.eval()。

        Batch Normalization（BN）在训练和测试阶段的行为不同。训练时，BN层对每个小批量数据计算均值和方差，用于归一化输入数据。同时，BN层会维护一个移动平均的全局均值和方差，用于测试阶段。  

训练阶段与model.train()

使用当前实时统计的批次统计量（均值、方差）进行归一化。这个统计量每个 forward 都重新算，不保存。

更新全局移动平均的均值和方差（不是 Parameter，不参与反向传播，所以 optimizer.step() 不会改它们，但 model.state_dict() 会保存）。只在训练 forward 时更新，进入 model.eval() 后彻底冻结。

应用可学习的缩放（γ）和偏移（β）参数（反向传播时由优化器负责刷新，与 BN 的“统计量”完全无关，“无关”指的是 梯度与数值不依赖统计量）。

测试阶段与model.eval()

使用训练阶段积累的全局移动平均均值和方差进行归一化。

停止更新统计量，保持固定。

仍应用训练好的γ和β参数。

BN层与Dropout层的关系

        Batch Normalization（BN）能够减少对Dropout的需求，尤其在深层网络中，主要归因于以下几个方面：

（1）正则化效果

        轻微噪声引入：BN在计算均值和方差时，基于mini-batch的统计量会引入轻微噪声，这种噪声类似于Dropout的随机性，起到一定正则化作用。

        参数缩放：BN通过归一化和重新缩放，使得模型对权重初始化不那么敏感，从而在一定程度上减少对Dropout的依赖。

（2）训练稳定性

        缓解梯度消失/爆炸：BN通过归一化输入，使得激活值的分布更加稳定，有助于缓解深层网络中的梯度消失或爆炸问题，从而提升训练稳定性。

        平滑优化景观：BN使得损失函数景观更加平滑，允许使用更大学习率，加速训练，减少对Dropout稳定训练过程的需求。

（3）模型性能

        提升收敛速度：BN加速模型收敛，使得训练过程更快达到较好性能，而Dropout可能因随机性导致训练时间延长。

        提高最终准确率：在某些情况下，BN通过稳定训练和提升收敛速度，能够达到比使用Dropout更高的最终准确率，尤其是在深层网络中。

（4） 深层网络中的优势

        保持表达能力：在深层网络中，BN通过稳定激活分布，有助于保持网络的表达能力，而Dropout可能因随机失活神经元而损失部分表达能力。

        避免过度依赖：随着网络加深，BN的归一化效果有助于避免对某些特征的过度依赖，类似于Dropout防止共适应的作用，但更高效。

       同时，BN层的隐式正则化与Dropout的显式正则化可能存在冲突。BN在训练时依赖批量统计量，而Dropout会随机改变神经元分布，可能干扰BN的标准化效果。

二者一起使用的时机：

（1）训练 batch-size ≥ 512（甚至 ≥ 1024）
原因：BN 的噪声强度 ∝ 1/m，m 大 → 噪声≈0，正则作用消失。
迹象：训练 loss 继续下降，验证 loss 提前回升，明显过拟合。
做法：在全局平均池化后的 1–2 层 FC 上加 Dropout(p=0.2–0.3)；卷积段仍不加。
（2）标注样本 < 10 k（小数据 / 医学 / 遥感）
原因：数据量小，BN 的 batch 统计量方差大，反而抖动剧烈；Dropout 的伯努利噪声更可控。
做法：
卷积段：BN 照常；
全连接段：FC → BN → ReLU → Dropout(p=0.3–0.5)。
若 GPU 内存允许，把 batch-size 压到 32–64，让 BN 噪声不过大。
（3）网络尾部存在大参数全连接层
典型：AlexNet/VGG 的 4096-d FC；ViT 的 MLP 头。
原因：FC 参数冗余度最高，共适应最严重；BN 对 FC 的分布平滑作用弱。
做法：FC₁ → ReLU → Dropout(0.5) → FC₂ → … → Softmax；BN 可选在 FC₁ 前。
（4）需要不确定性估计（MC-Dropout）
场景：医学诊断、自动驾驶、异常检测。
原因：BN 推理期统计量固定，无法通过随机性生成置信区间；Dropout 可继续在推理期采样。
做法：
训练期：BN + Dropout 正常共存；
推理期：保持 Dropout 开，跑 T≈20–50 次前向，得到预测分布。
（5）迁移学习 / 微调阶段
原因：预训练模型已收敛，BN 噪声≈0；新数据往往更小，易过拟合。
做法：冻结主干 BN，仅微调头部；在新增 FC 后加 Dropout(p=0.3)。