折半(二分)查找

前言:

折半查找是一种高效且简单的查找算法，每次做题的时候边界容易被混淆。本文提供一种方法“红蓝染色法”。

注意:

使用折半查找(二分查找)时，数组必须是有序的

例:

给定一个非递减排列有序的数组:nums=[5,7,7,8,8,10],target=8,找到第target的起始索引和结束索引

暴力:

这种题，我还是喜欢先看看暴力能不能做。很显然暴力在这里是适用的。就是依次枚举，遇到就记录，直到出现大于target的数，停止循环

def searchRange(nums, target):
    li = []
    for i in range(len(nums)):
        if nums[i] == target:
            li.append(i)
        elif nums[i] > target:
            break
    if len(li) == 0:
        return [-1, -1]
    else:
        return [li[0], li[-1]]


if __name__ == '__main__':
    nums = [5, 7, 7, 8, 8, 10]
    target = 8
    print(searchRange(nums, target))

 Python是世界上最好的语言，但是就是容易超时唉

折半:

什么是折半查找喃，听其名，明其意。就是初始时以左右两端点为起始点。每次取其中间值，然后与target进行比较。这样我们每次就知道了一半数据的大小。下次查询的时候就可以直接将不符合题意的那一半给舍弃。

 

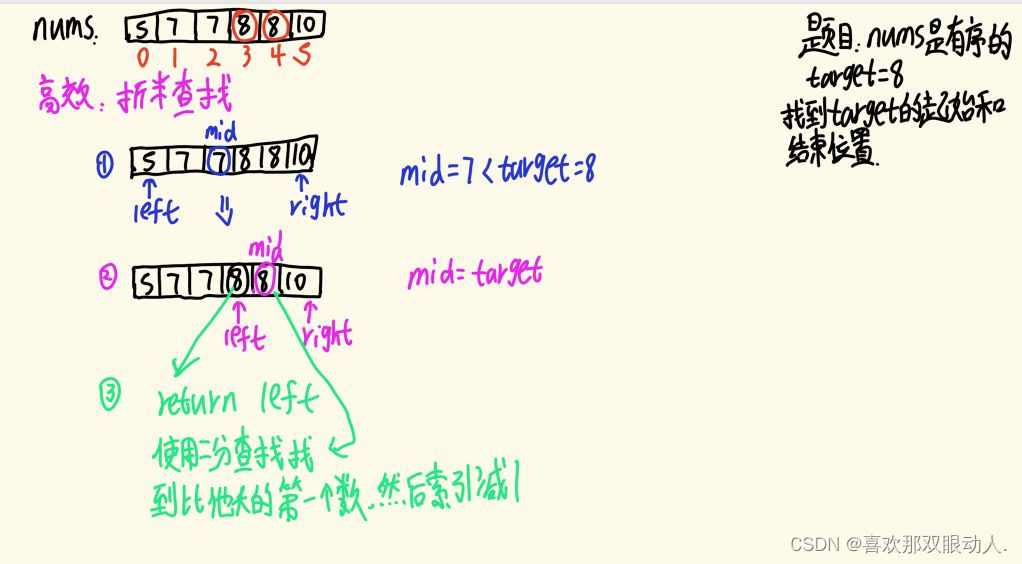
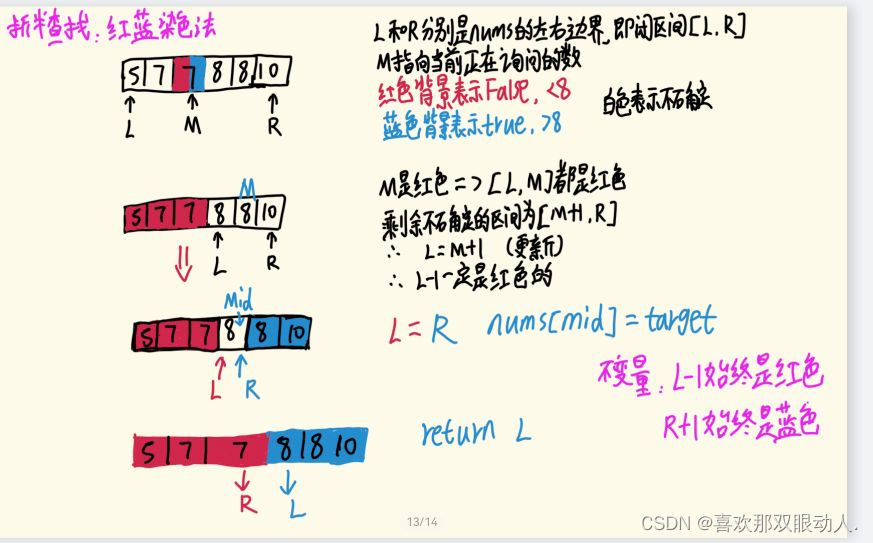
 为什么每次都更新都是:L=M+1(R=M-1)呢？而不是更新为:L=M(R=M)?

 Leetcode:34. 在排序数组中查找元素的第一个和最后一个位置

https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/

思路见上述图

 代码:

def Binary_lookup(nums, target):
    left = 0
    right = len(nums) - 1
    while left <= right:
        mid = (left + right) // 2  # 每次取中间值
        if nums[mid] < target: #比较
            left = mid + 1
        else:
            right = mid - 1
    return left


def searchRange(nums,target):
    # 非递减顺序排列的整数数组
    # 目标值在数组中的开始位置和结束位置
    # 如果数组中不存在目标值 target，返回 [-1, -1]
    # 时间复杂度为 O(log n)
    start = Binary_lookup(nums, target)
    if len(nums) == 0 or nums[start] != target:  # 如果数组是一个空数组或者数组中根本就没有这个数
        return [-1, -1]
    else:
        end = Binary_lookup(nums, target + 1) - 1
        return [start, end]

 为什么end = Binary_lookup(nums, target + 1) - 1,最后target要先arget + 1然后在减去1？

折半模板:

        1.[left,right]  左闭右闭型

        2.[left,right) 左闭右开型

         3.(left,right) 左开右开型

def Binary_lookup_one(nums, target):  # 左闭右闭
    left = 0
    right = len(nums) - 1
    while left <= right:
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return left


def Binary_lookup_two(nums, target):  # 左闭右开
    left = 0
    right = len(nums) - 1
    while left <= right:
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid + 1
        else:
            right = mid
    return left


def Binary_lookup_three(nums, target):  # 左开右开
    left = 0
    right = len(nums) - 1
    while left <= right:
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid
        else:
            right = mid
    return left

 在一个有序序列中查找一个数的前继或者后继:

1.在单调序列a中查找<=x的数的最大一个,即x的前继

def Find_successor_qian(nums,target):
    left=0
    right=len(nums)-1
    while left<right:
        mid=(left+right+1)//2
        if nums[mid]<=target:
            left=mid
        else:
            right=mid-1

 2.在单调序列a中查找>=x的数的最小一个,即x的后继

def Find_successor_hou(nums,target):
    left=0
    right=len(nums)-1
    while left<right:
        mid=(left+right)//2
        if nums[mid]>=target:
            right=mid
        else:
            left=mid+1