蛇形填充数组

期末程序考试结束了，其中一道是这个题

简单写一下规律：

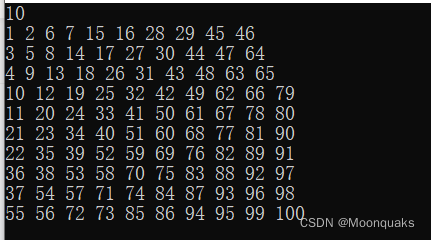
以10为例

奇数 左下->右上

偶数 右上->左下

分成两个部分：//1.左上三角形部分，编号为1~n

//2.右下三角形部分，编号n+1~2n-1

用k计数,从1开始，用i表示赋值，从1开始

第一部分：

k为奇：循环kk=k-1;kk>=0;kk--

num[kk][k-1-kk]=i;

k为偶数：

kk=k-1;kk>=0;kk--

num[kk][k-1-kk]=i;

第二部分：(顺着加过去)

k为奇数：

kk=n-1,kk>=k-n;kk--;

num[kk][k-kk-1]-=i;

k为偶数：

kk=n-1,kk>=k-n;kk--;

nunm[k-kk-1][kk]=i;

之前想过很多，行列的关系，其实就是第一部分，行数+列数=k-1；

第二部分，行数+列数=k-1;

都是k-1！

而且奇数偶数也只是换了一下行列 罢了

甚至，是不是可以将两个部分合在一起呢？（简化不了多少，也就是在奇数（偶数）里面在多一个判断）

（可不可以在第一部分看完之后，第二部分从n^2看呢？）

总之就是找规律蛮简单

后续会有一元三次方程求解

告辞