1.

#include<stdio.h>
typedef long long LL;
LL m,n,k,l;
int main(){
scanf("%lld %lld %lld %lld",&n,&m,&k,&l);
if(m>n||k+l>n){ //看下文,第一个条件是有一点重复的
printf("-1");
return 0;
}
LL cnt=(k+l)/m;
if((k+l)%m){
cnt+=1;
}
if(cnt*m>n){
printf("-1");
return 0;
}
printf("%lld",cnt);
return 0;
}【我决定用费曼技巧来写博客了,就是说以教促学】
题干
伊万正在收集硬币。只有NN种不同的可收藏硬币,伊万有KK。他很快就会庆祝他的生日,所以他所有的MM朋友都决定送给他硬币。他们都同意了三个条款:
每个人都必须赠送与其他人一样多的硬币。(1)
所有送给伊凡的硬币都必须是不同的。(2)
不少于LL硬币从礼物中完全,必须是伊万收藏的新品。(3)
但他的朋友们不知道伊万收藏了哪些硬币。他们不想花钱,所以他们想购买最少量的硬币,这些硬币满足所有条款,而不管伊万的收藏如何。帮助他们找到这个最小数量的硬币或定义它不可能满足所有条款。
唯一的输入行包含 4 个整数 NN, MM, KK, LL (1 le K le N le 10^{18}1≤K≤N≤10
18
;1 le M, ,, L le 10^{18}1≤M,L≤10
18
) — 不同硬币的数量、伊凡的朋友数量、伊万收藏的大小和硬币的数量,这些硬币必须是伊凡收藏中的新硬币。
打印一个数字 - 一个朋友可以赠送的最小数量的硬币,以满足所有条件。如果不可能满足所有三个条件,请打印"-1"(不带引号)。
解析:
(1):每一个人送的硬币个数一样,m个人就是,每个人送x个,总共送出去就是m*x个。
(2)每一个硬币必须不同:一共送了m*x个,硬币的总种类又是n种,一个判定条件为m*x<=n;
(3)不少不l个式新品,这里需要仔细思考一下,我们得确保新品不少于l个,而伊万已经有了k个,那么能确保的最低送出去个数就是l+k个了;
(4)由于输入是随机的,我们也需要考虑那种乍一看就不符合条件的输入,比如:
1°每个人最低送一个吧,人如果很多,总共m个都超过了n,那岂不是一定会有重复的,排除
2°如果我们最低送出去的个数l+k大于n也是要重复的,排除。
(这里有很多情况,比如l不能大于n,k也不能大于n,和2°是一样的)
(我刚刚也在想1°是不是会重复,确实重复了!我把它标记一下)
所以我么总的思路就是,在l+k<=n的前提下,我们最少需要l+k个不同的硬币。而这些硬币,需要m个人中每个人都出相同的数目。如果恰好除尽(每个人最后算出来的数目是整数)就好办,如果不是呢?就需要人均再出一个硬币了。
这样就会有一个问题,刚刚我们是算的cnt*m<=n,那我们这里的总数也应该小于等于n啊(2)
(我又在想,那2°岂不是也重复了,确实重复了!标记一下)
你们知道怎么重复了吗?思考后看下文!
紫色这段话我们可以得到,要不刚好除尽,我们出l+k个,要不还有剩余我们就会得l+k+m个,总之就是我们最终的个数>=l+k,而我们也要判断最终个数<=n,那还要l+k<=n干嘛呢?
于是乎最后答案变成了:这样!
原来我是看的别人的回答,现在自己想想,也有了新的思考。
#include<stdio.h>
typedef long long LL;
LL m,n,k,l;
int main(){
scanf("%lld %lld %lld %lld",&n,&m,&k,&l);
LL cnt=(k+l)/m;
if((k+l)%m){
cnt+=1;
}
if(cnt*m>n){
printf("-1");
return 0;
}
printf("%lld",cnt);
return 0;
} 2.

我开始下手也是想了很久,后面看了一篇文章才点到我了
这是一个循环的问题(当然可以写成递归,我待会试试),那我们就要来分析其中的变与不变(如果想不到这里,就去看看递归啊啥的,我这里不再赘述)
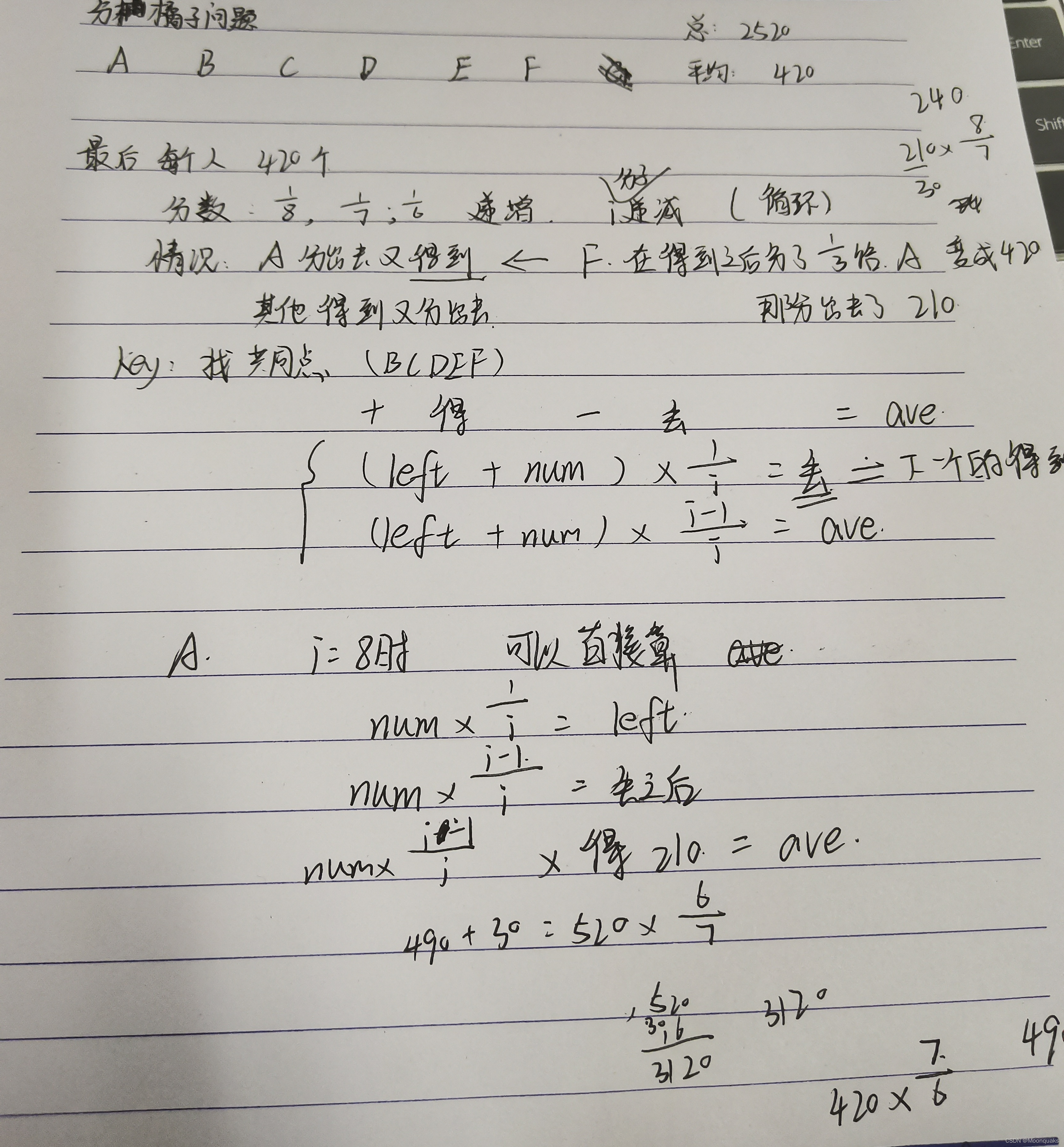
这是我随手写的,我还是要分析的啊!!(看图吧)
A是先分出去给B,最后从E那里得到,而其他的就是先从前一个那里得到,然后给下一个。
所以,A就很特殊啦!我们甚至可以直接得出A好吧(根据E最后分出去1/3后剩下AVE,算一下就可以了)
A得到之后我们需要的就是把A和其他联系起来,中间媒介就是A分给B的left,已知条件又有一个最后每一个AVE,就很容易建立方程求解,这是数学上的。把他写成代码需要我们将未知量(需要求的)移到左边。
大致代码如下:
#include<stdio.h>
#define AVE 420
int main(){
int num,i,left;
for(i=0;i<=5;i++){
if(i==0){
num=((AVE-AVE/2)*(8-i))/(8-i-1);
left=num/(8-i);
}
else{
num=(AVE*(8-i))/(8-i-1)-left;
left=(num+left)/(8-i);
}
printf("第%d个兄弟原来的橘子为%d个\n",i+1,num);
printf("%d\n",i);
}
return 0;
}
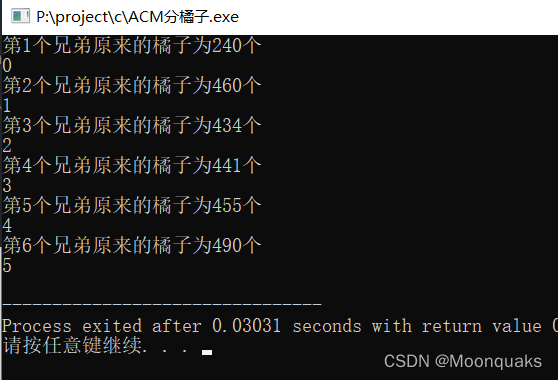
写的时候我发现了一个问题就是,整除真的很要命啊,有人如果知道怎么有效解决这个问题,不妨评论或者私聊我一下!
就是这样!
告辞!
























 1463
1463

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








