2025年5月6日

欠驱动机器人学-麻省理工学院开放课程-MIT 6.832: Underactuated Robotics（译）_underactuated robotics mit-优快云博客

欠驱动的官网

 

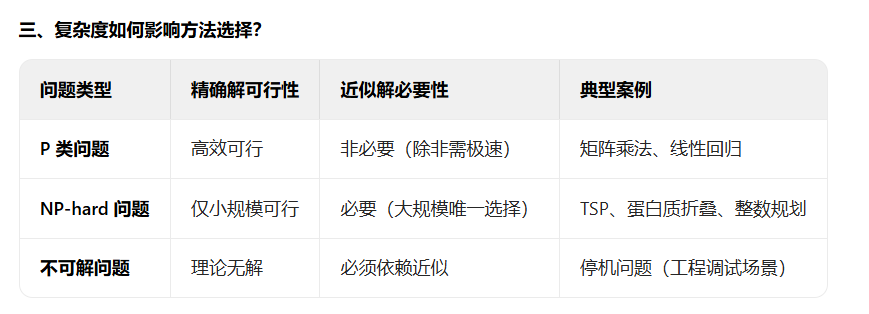
精确解（Exact Solution）

• 定义：在给定问题的条件和约束下，能够严格满足所有方程、边界条件或逻辑关系的解，不存在任何误差或近似假设。
• 本质特征：
  • 解与真实结果完全一致（如代数方程的解析解、几何问题的严格推导结果）。
  • 通常通过解析方法（如公式推导、符号运算）获得，依赖问题的结构化和可解性。
• 典型示例：
  • 一元二次方程 \(ax^2 + bx + c = 0\) 的求根公式（精确解为 \(\frac{-b \pm \sqrt{b^2-4ac}}{2a}\)）。
  • 物理中理想单摆的周期公式（忽略空气阻力和摆角限制时的精确解）。

2. 近似解（Approximate Solution）

• 定义：当精确解不存在、难以求解或计算成本过高时，通过简化假设、数值方法或经验模型得到的接近真实解的结果，允许存在可控误差。
• 本质特征：
  • 基于 “可接受误差范围内逼近真实解” 的目标，通过近似方法（如泰勒展开、有限差分、蒙特卡洛模拟）实现。
  • 解的精度可通过误差分析（如绝对误差、相对误差）量化，并根据需求调整