代码随想录刷题攻略---回溯1---回溯理论基础+组合

本文链接：https://blog.youkuaiyun.com/qq_54990658/article/details/143261198

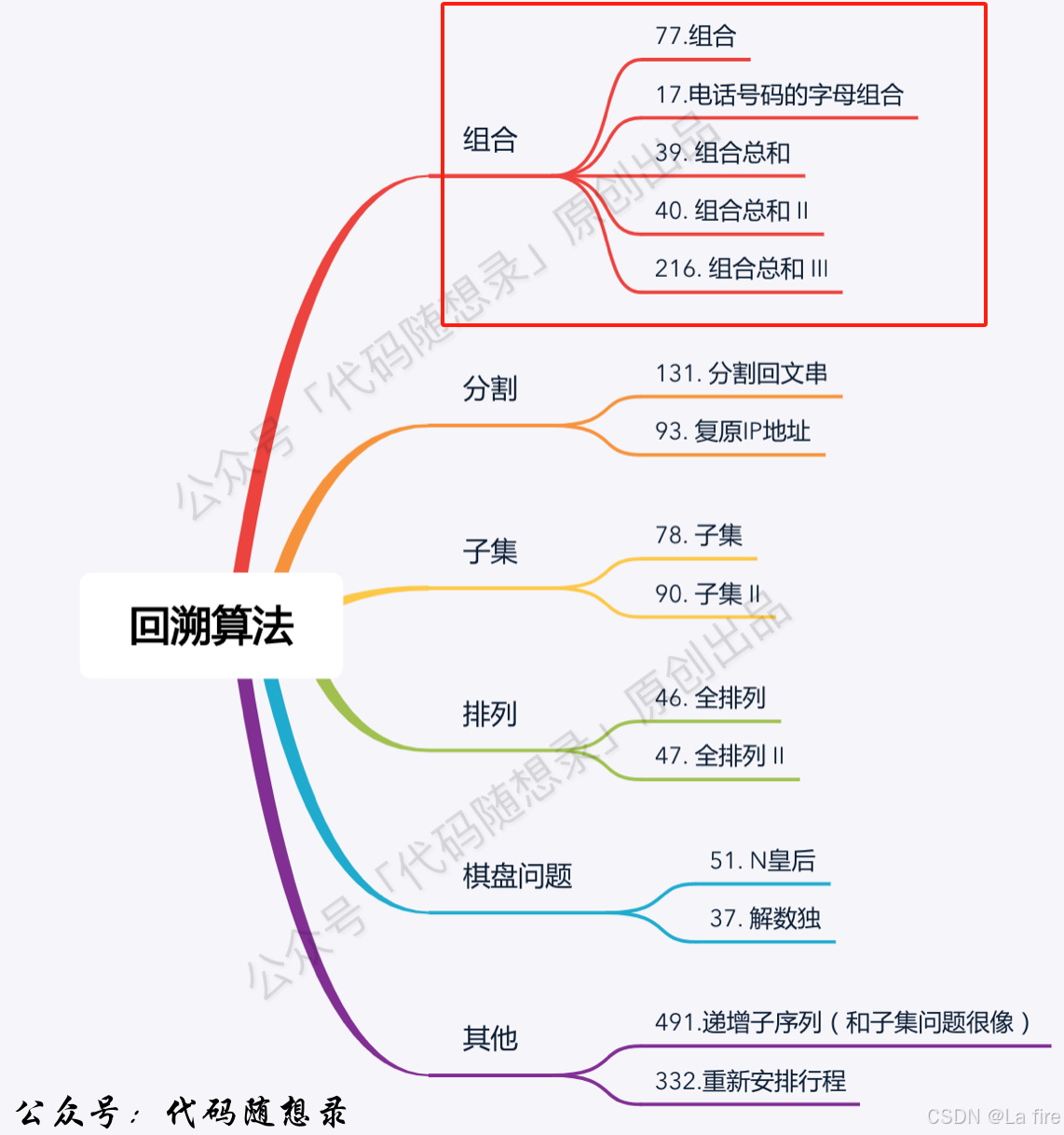
回溯题型：

回溯法——递归的副产物

（我的老师认为，回溯是一种目的，递归是实现目的的手段）

回溯法的本质是用穷举实现搜索目的，使用回溯法进行搜索的场景一般比较复杂，能解出来就不错了，如：

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等

对于这些问题，回溯法的搜索过程可以理解为 对一颗N叉树的递归搜索，因为其搜索的是集合中递归寻找满足条件的子集组合/排列。而对于每一颗子树的递归，都会有一个终止条件（即搜索到叶子结点了，再往下就没有其它可能了），可以表示为

if(目前搜索到了终止条件)
{
    整理该条路径的搜索结果；
    return；（回到上一层结点去，看看有没有其他可能的走法）
}

因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来，所以一般是先写逻辑，然后需要什么参数，就填什么参数。

这张图直观地表示了搜索方向、递归、回溯，搜索方向是从左到右搜索每颗子树（子集），递归是选取好1个结点后继续往深处搜索后续的组合/排列，当前递归结束时，会回溯到上一层继续搜索。

递归的过程如下：

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

回溯法总伪代码：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

组合问题：

例题1：组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

递归函数的返回值以及参数

在这里要定义两个全局变量，一个用来存放符合条件单一结果，一个用来存放符合条件结果的集合

其实不定义这两个全局变量也是可以的，把这两个变量放进递归函数的参数里，但函数里参数太多影响可读性，所以我定义全局变量了。

    vector<vector<int>> res; 
    vector<int> tmp;

然后还需要一个参数，为int型变量startIndex，这个参数用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,...,n] ），防止出现重复的结果。

回溯函数终止条件

当我们的tmp数组的容量达到 k 时，说明我们已经从根结点搜到叶子结点了，可以把这个结果保存进 res 里，再进行回溯。

if(tmp.size() == k)
{
    res.push_back(tmp);
    return;
}

单层搜索的过程

for循环每次从start开始遍历，然后用 tmp 保存取到的节点 i 。

class Solution {
public:
    vector<vector<int>> res; 
    vector<int> tmp; 
    void backtracking(int n, int k, int start)
    {
        if(tmp.size() == k)
        {
            res.push_back(tmp);
            return;
        }

        for(int i = start; i <= n; i++)
        {
            tmp.push_back(i);
            backtracking(n,k,i+1);
            tmp.pop_back();//回溯
        }
    }

    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return res;
    }
};

这个代码还可以进行剪枝优化，比如当 n=4,k=4 时，start只有为 1 的时候符合条件，为 2,3,4 的长度都不够。

已经选择的元素个数：tmp.size()
所需需要的元素个数为: k-tmp.size()
列表中剩余元素 (n-i) >= 所需需要的元素个数 (k-tmp.size())
在集合n中至多要从该起始位置 (i <= n - k - tmp.size() + 1) 处开始遍历。 +1 是因为我们包括起始位置。举例 n=4,k=4，我们要从起始位置 1 而不是 0 开始遍历。

例题2：组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

终止条件：

if(target <= 0)
        {
            if(target == 0)//处理
                res.push_back(tmp);
            return ;//返回
        }

单层循环：要注意一下 index 是可以跟当前元素重复的

class Solution {
public:
    vector<int> tmp;
    vector<vector<int>> res;
    void backtracing(vector<int>& candidates, int target , int index)
    {
        if(target <= 0)
        {
            if(target == 0)//处理
                res.push_back(tmp);
            return ;//返回
        }
        for(int i = index; i< candidates.size(); i++){
            tmp.push_back(candidates[i]);
            backtracing(candidates, target-candidates[i], i);// 关键点:不用i+1了，表示可以重复读取当前的数
            tmp.pop_back();
        }
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        backtracing(candidates, target, 0);
        return res;
    }
};

剪枝策略：当 candidates 有序时，对于 sum 已经大于 target 的情况，其实是依然进入了下一层递归，只是下一层递归结束判断的时候，会判断 sum > target 的话就返回。所以我们在循环条件中可以加上 sum与当前元素的和是 <= target值的。

例题3：组合总和II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

这道题跟上一道很不一样，本题candidates 中的每个数字在每个组合中只能使用一次，且candidates是有重复元素的。carl在这里提出了 2 个新概念，“树层”和“树枝”：

在这个题中，一个树枝上可以使用值相同的元素，但同一个树层不可以使用值相同的元素；所以我们可以用1个布尔型的数组来区分某个位置的值有没有被使用。

传参、递归终止条件跟上一题类似，只是传参多传了一个 bool 类型的数组。
单层循环逻辑：主体还是与上一题类似，只是我们多加了去重的操作；怎么做的呢，同一树层我们已经排好序了，只要判断当前元素是否跟前一个元素相同就可以了，如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]，此时for循环里就应该做continue的操作。一条树枝上可以使用值相同的数字，

我们在递归前，会将当前的位置的 used 数组设置为 true，表示可以重复选取的状态；回溯后，把当前的位置的 used 数组设置为 false，表示无法重复选取的状态。

“可能有的录友想，为什么 used[i - 1] == false 就是同一树层呢，因为同一树层，used[i - 1] == false 才能表示，当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。”

class Solution {
public:
    vector<vector<int>> res;
    vector<int> tmp;
    
    void backtracking(vector<int>& candidates, int target, int index, vector<bool>& used){
        if(target <= 0){
            if(target == 0)
                res.push_back(tmp);
            return ;
        }
        //树枝可以有重复数字，数层不能有
        for(int i = index; i < candidates.size(); i++)
        {
            if(i > 0 && candidates[i] == candidates[i-1] && used[i-1] == false)//没有树枝使用这个数，即，此状态不能有重复元素
                continue;
            tmp.push_back(candidates[i]);
            used[i] = true;//树枝上使用了 i 位置上的数
            backtracking(candidates, target-candidates[i], i+1, used);
            used[i] = false;//已回溯，证明此树枝上没人用了
            tmp.pop_back();
        }
    }

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<bool> used(candidates.size(),false);
        sort(candidates.begin(), candidates.end());
        backtracking(candidates,target,0,used);
        return res;
    }
};

例题4：数字分组求偶数和

问题描述

小M面对一组从 1 到 9 的数字，这些数字被分成多个小组，并从每个小组中选择一个数字组成一个新的数。目标是使得这个新数的各位数字之和为偶数。任务是计算出有多少种不同的分组和选择方法可以达到这一目标。

numbers: 一个由多个整数字符串组成的列表，每个字符串可以视为一个数字组。小M需要从每个数字组中选择一个数字。

例如对于[123, 456, 789]，14个符合条件的数为：147 149 158 167 169 248 257 259 268 347 349 358 367 369。

import java.util.ArrayList;
import java.util.List;

public class Main {
    public static int solution(int[] numbers) {
        // Please write your code here
        List<List<Integer>> groups=new ArrayList<>();
        for(int nums:numbers)
        {
            List<Integer> group=new ArrayList<>();
            while (nums > 0) {
                group.add(nums % 10);
                nums /= 10;
            }
            groups.add(group);
        }
        
       int count = backtrack(groups,0,0);

        return count;
    }

    public static int backtrack(List<List<Integer>> groups, int l, int r)
    {
        if(l==groups.size())//终止条件
        {
            if(r%2==0)//判断当前和是否为偶数
                return 1;
            else
                return 0;
        }//结束当前递归
        int count=0;
        for(int num:groups.get(l))//取数字组 循环遍历
        {
            count+=backtrack(groups, l+1, r+num);//count为偶数组合的个数,递归
        }
        return count;
    }

    public static void main(String[] args) {
        // You can add more test cases here
        System.out.println(solution(new int[]{123, 456, 789}) == 14);
        System.out.println(solution(new int[]{123456789}) == 4);
        System.out.println(solution(new int[]{14329, 7568}) == 10);
    }
}