代码随想录刷题攻略--二叉树2--二叉树的属性

 二叉树1过了一遍“二叉树的遍历方式”，现在开始过二叉树2：二叉树的属性。

 例题1：对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

 对于二叉树是否对称，要比较的是根节点的左子树与右子树是不是相互翻转的，理解这一点就知道了其实我们要比较的是两个树（这两个树是根节点的左右子树），所以在递归遍历的过程中，也是要同时遍历两棵树。

什么时候只能使用后序遍历：需要我们先收集左右孩子的信息，收集完毕了再向上一层返回结果的题型只能用后序遍历。我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。如果是前序或者中序的话，还没完全得到2个子树的结果就return了。

递归3部曲：

1、确定递归函数的参数和返回值

传入2个当前树结点指针即可，观察2个树结点对应的结点值是否一致，一致则返回 true，否则返回false;

bool compare(TreeNode* left, TreeNode* right)

2、确定结束条件

当前2个指针指向的树结点的值不相等时，结束循环。不过此时还要额外处理一下当指针都指向（单个指向）null的情况；

if(left == NULL && right == NULL)
    return true;
else if(left == NULL)
    return false;
else if(right == NULL)
    return false;
else if(right -> val == left -> val)
    return true;
else
    return false;

 注意，其实我写的倒数第二种情况是不对的；因为此刻仍然还有左右子树，不能草率地返回true，正确代码：

if(left == NULL && right == NULL)
    return true;
else if(left == NULL)
    return false;
else if(right == NULL)
    return false;
else if(right -> val ！= left -> val)
    return false;

3、确定单层递归的逻辑

单层递归中，先判断2个树结点对应的结点值是否一致，一致则返回 true，否则返回false.

单层递归的逻辑就是处理 左右节点都不为空，且数值相同的情况。

• 比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
• 比较内侧是否对称，传入左节点的右孩子，右节点的左孩子。
• 如果左右都对称就返回true ，有一侧不对称就返回false 

bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右
bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左
bool isSame = outside && inside;                    // 左子树：中、 右子树：中（逻辑处理）
return isSame;

 整体代码

class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right) {
        if(left == NULL && right == NULL)
            return true;
        else if(left == NULL)
            return false;
        else if(right == NULL)
            return false;
        else if(right -> val ！= left -> val)
            return false;
        // 此时就是：左右节点都不为空，且数值相同的情况
        // 此时才做递归，做下一层的判断
        bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右
        bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左
        bool isSame = outside && inside;                    // 左子树：中、 右子树：中 （逻辑处理）
        return isSame;

    }
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        return compare(root->left, root->right);
    }
};

例题2： 另一棵树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

 这题跟上一题有点像，代码如下

class Solution {
public:
    bool com(TreeNode* root, TreeNode* subRoot)
    {
        if(root == NULL && subRoot == NULL)
            return true;
        else if(root == NULL)
            return false;
        else if(subRoot == NULL)
            return false;
        else if (root->val != subRoot->val) {
            return false;
        }

        bool res = com(root->left, subRoot->left) && com(root->right, subRoot->right);
        return res;
    }

    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if (root == nullptr) {
            return false;
        }
        return com(root, subRoot) || isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
    }
};

 因为要先判断 root 跟 subRoot 的左右子树情况，所以这题仍然也是用后序遍历处理。

不同的是，此题的 root 结点会发生变化，即 root 会移动到左子树或者右子树上，判断以新的 root作为根的子树是否跟 以subRoot 为根节点的树一致。

难的部分在于，我们要把 isSubtree 当作一个递归函数，直接用这个函数遍历二叉树 root 的结点。

在代码里，isSubtree 的职责就是判断 subRoot 是不是 root的子树， 是不是 root 左子树中的子树，是不是 root 右子树中的子树。所以递归函数 isSubtree 的单层逻辑就是：

bool isSubtree(TreeNode* root, TreeNode* subRoot) {
     if (root == nullptr) {
        return false;
      }
      return com(root, subRoot) || isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
    }

而 com 函数的职责就是判断 root 和 subRoot 两棵树是否一致。

例题3： 二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

 在做此题前，先弄清楚树的深度和高度的区别。

深度：二叉树里任意1个结点到根结点的距离

高度：二叉树中任意结点到叶子结点的距离

如果是求深度，应该使用前序遍历，先计算上层数量。

如果是求高度，应该使用后序遍历，先计算子树的高度，从下往上去计数。

class Solution {
public:
    int Depth(TreeNode* root, int depth) {
        if(root == NULL)
            return depth;//结点为空，表示这个子树的深度不再计算
        depth++;//继续往下找一层
        int l = Depth(root->left, depth);
        int r = Depth(root->right, depth);
        return max(l,r);
    }

    int maxDepth(TreeNode* root) {
        if(root == NULL)
            return 0;//结点为空，表示深度为0
        int res = Depth(root, 0);
        return res;
    }
};

例题4：二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

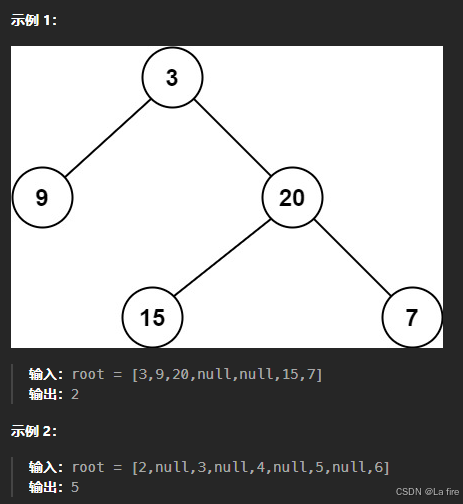
 这道题跟上一题有点像，但是如果单纯把

return max(l,r);

改为

return min(l,r);

是错误的，因为如果一颗二叉树只有右子树没有左子树，结果会直接返回1而不是右子树的深度。

所以当左子树或者右子树为空时，要进行单独处理。

class Solution {
public:
    int Depth(TreeNode* root, int depth)
    {   
        if(root==NULL)//终止条件
            return depth;
        int l = depth+1;//左子树和右子树的最小深度初始化
        int r = depth+1;
        if (!root->left && !root->right)
            return min(l,r);
        if(root->left && !root->right)//只有左子树，那么只搜索左子树的最小深度并返回
        {
            l=Depth(root->left,depth+1);
            return l;
        }
        if(!root->left && root->right)
        {
            r=Depth(root->right,depth+1);
            return r;
        }
        //两边都有
        return min(Depth(root->left,depth+1), Depth(root->right, depth+1));
    }

    int minDepth(TreeNode* root) 
    {
        if (root == NULL)
            return 0;
        return Depth(root, 0);
    }
};

例题5：平衡二叉树

给定一个二叉树，判断它是否是平衡二叉树（左右子树的高度之差不超过1）

单层逻辑：当传来一个树结点指针 root 时，我们会判断其左子树和右子树的高度之差是否符合平衡二叉树的定义，如果不符合，直接返回-1表示这棵树存在不平衡的状态；如果符合，我们会返回以 root 为根结点的树的最大高度，给上一级判断提供参考。

class Solution {
public:
    int is(TreeNode* root) {
        if(root == NULL)
            return 0;
        
        int l = is(root -> left);//左
        if(l == -1) return -1;
        int r = is(root -> right);//右
        if(r == -1) return -1;

        //根
        if(abs(l-r)>1)
            return -1;
        return 1+max(l,r);// 以当前节点为根节点的树的最大高度
    }
    bool isBalanced(TreeNode* root) {
        int res = is(root);
        return res == -1 ? false : true;
    }
};

 例题6：二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

这一题中，因为要使用vector穿梭多个调用层中搜集路径信息，所以我们的递归函数会用到vector的引用，由于输出是 string 类型，结点是整型，所以我们使用2个数组，1个用来装整数路径，1个在遍历到叶子结点时整合这条路径为 string 类型。

void Traverse(TreeNode *tree, vector<int> &path, vector<string> &res)

由于我们的路径是从根结点到叶子结点搜集的，所以这一题我们使用前序遍历。

对于终止条件，我们发现root的左右孩子都为NULL时，说明我们当前的路径遍历到头了。

这个时候我们将 path 数组里的信息都转换为 string 类型，装入我们的 res 里：

if(root -> left == NULL && root ->right == NULL)
{
   string sPath;
   for (int i = 0; i < path.size() - 1; i++) { // 将path里记录的路径转为string格式
      sPath += to_string(path[i]);
      sPath += "->";
    }
    sPath += to_string(path[path.size() - 1]); // 记录最后一个节点（叶子节点）
    res.push_back(sPath); // 收集一个路径
    return;
};

单层循环逻辑：由于我们的终止条件只判断了 root 的左右孩子， 所以我们在单层循环逻辑中要判断一下 下一个遍历结点是否是NULL；

遍历完某一结点的左右孩子后，我们就收集完了 2 条以该结点为经历点的路径，我们需要返回到上一层，遍历以其它结点为经历点的路径（这个过程就是回溯过程），整体代码如下：

class Solution {
public:
    void Traverse(TreeNode* root, vector<int> &path, vector<string> &res)
    {
        path.push_back(root -> val);//根,为什么写在这里，因为叶子结点也要加入到path中;否则遍历到叶子结点就直接统计路径信息了
        if(root -> left == NULL && root ->right == NULL)
        {
            string sPath;
            for (int i = 0; i < path.size() - 1; i++) { // 将path里记录的路径转为string格式
                sPath += to_string(path[i]);
                sPath += "->";
            }
            sPath += to_string(path[path.size() - 1]); // 记录最后一个节点（叶子节点）
            res.push_back(sPath); // 收集一个路径
            return;
        };
        
        if(root->left)//左
        {
            Traverse(root->left,path,res);
            path.pop_back();
        }
        if(root->right)//you7
        {
            Traverse(root->right,path,res);
            path.pop_back();
        }
        
    }

    vector<string> binaryTreePaths(TreeNode* root) 
    {
        vector<string> result;
        vector<int> path;
        if (root == NULL) return result;
        Traverse(root, path, result);
        return result;
    }
};

例题7：左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

我使用了一个全局res来计算所有左叶子的和，所以递归只需要传入结点指针即可。

终止条件：当当前结点为NULL,返回。

单层逻辑：当我们判断出当前结点可以有左叶子时。如下图，当前结点为 9 ，我们判断它有左叶子，此时就可以增加 res 值（注意，此时并不是终止条件，因为我们还要去 9 的右子树里看看有没有左叶子。），增加/不增加后，我们继续探索 root 的左子树和右子树。

class Solution {
public:
    int res = 0;
    void Traverse(TreeNode* root)
    {
        if(root == NULL)
            return;

        if(root -> left && root -> left -> left == NULL && root -> left -> right == NULL)//找到某个结点的左叶子了
        {
            res += root ->left ->val;
            //return ; 这里不能return 如果发现当前结点有左叶子就return 就会忽略 root->right 可能存在的左叶子
        }

        //往左找
            Traverse(root->left);
        //往右找
            Traverse(root->right);
    }

    int sumOfLeftLeaves(TreeNode* root) 
    {
        if(root == NULL) return 0;
        //if(root -> left == NULL) return 0; 这里不对 可以去 root 的右子树里找其它左叶子
        Traverse(root);
        return res;
    }
};

例题8：找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

 这道题可以用层序遍历来做，方法简单：

class Solution {
public:
    TreeNode *res;
    int findBottomLeftValue(TreeNode* root) {
        res = root;
        queue<TreeNode *> que;
        que.push(root);
        while(!que.empty())
        {
            int size = que.size();
            for(int i = 0; i < size; i++)
            {
                if(i==0) res = que.front();
                TreeNode *p = que.front();
                if(p->left)
                    que.push(p->left);
                if(p->right)
                    que.push(p->right);
                que.pop();
            }
        }
        return res->val;
    }
};

用递归比较难，递归函数的参数为树结点指针以及当前深度（找最大深度用），无返回值。

终止条件：当遇到叶子节点的时候，就需要统计一下最大的深度了，所以需要遇到叶子节点来更新最大深度。

if(root->left==NULL && root->right==NULL)
{
    maxDepth = max (maxDepth, depth); // 更新最大深度
    result = root->val;               // 最大深度最左面的数值
    return;
}

单层逻辑：若当前结点 root 有左子树，我们将当前的搜索深度加1，继续搜索树最左下角的值，然后再恢复一下当前搜索深度(减1)。

class Solution {
public:
    int maxDepth = INT_MIN;
    int result;
    void traversal(TreeNode* root, int depth) {
        if (root->left == NULL && root->right == NULL) {
            if (depth > maxDepth) {
                maxDepth = depth;
                result = root->val;
            }
            return;
        }
        if (root->left) {
            depth++;
            traversal(root->left, depth);
            depth--; // 回溯
        }
        if (root->right) {
            traversal(root->right, depth++);//精简版，跟上面的一样
        }
        return;
    }
    int findBottomLeftValue(TreeNode* root) {
        traversal(root, 0);
        return result;
    }
};