开始学最不愿面对的一章。。。
动态规划理论基础
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的。
按照carl所说,他将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
动态规划应该如何debug?
找问题的最好方式就是把dp数组打印出来,看看究竟是不是按照自己思路推导的!
一些同学对于dp的学习是黑盒的状态,就是不清楚dp数组的含义,不懂为什么这么初始化,递推公式背下来了,遍历顺序靠习惯就是这么写的,然后一鼓作气写出代码,如果代码能通过万事大吉,通过不了的话就凭感觉改一改。
这是一个很不好的习惯!
做动规的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,确定最后推出的是想要的结果。
例题1:爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
- 输入: 2
- 输出: 2
- 解释: 有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2:
- 输入: 3
- 输出: 3
- 解释: 有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
动规五部曲
1.确定dp数组以及下标的含义
dp[i]:有 i 阶楼梯时,有 dp[i] 种方法爬完
2.确定dp数组递推式
dp[i] = dp[i - 1] + dp[i - 2],
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和。
3.dp数组初始化
题目种说 n 是正整数,所以不考虑 n=0 的情况。
由例子可以知道 dp[1] = 1, dp[2] = 2。
4.确定遍历顺序
由递推公式 dp[i] = dp[i - 1] + dp[i - 2] 可知,dp[i]都是从其下方推导而来。
5.手动写几个dp[i][j]推导验证一下

code
class Solution {
public:
int climbStairs(int n) {
if(n<=2)
return n;
vector<int> dp(n + 1);
dp[1] = 1;
dp[2] = 2;
for(int i = 3; i <= n; i++)
{
dp[i] = dp[i-1] + dp[i-2];// 注意i是从3开始的
}
return dp[n];
}
};例题2:使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。

动规五部曲
1.确定dp数组以及下标的含义
dp[i]:有 i 阶楼梯时,向上爬需要支付的最小费用。
2.确定dp数组递推式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i] = min(dp[i - 1] + cost[i-1], dp[i - 2] + cost[i-2])
3.dp数组初始化
题目说可以从 0 或者 1 阶梯开始爬,所以dp[0] = 0, dp[1]= 0.
4.确定遍历顺序
由递推公式可知,dp[i]都是从其下方推导而来。
5.手动写几个dp[i][j]推导验证一下
code
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();//一共n层楼梯
if(n == 0 || n == 1) return 0;
vector<int> dp(n+1);
dp[0]=0;
dp[1]=0;
for(int i = 2; i <= n; i++){
dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);
}
return dp[n];
}
};例题:不同路径
一个机器人位于一个 m x n 网格的左上角。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角。
问总共有多少条不同的路径?

这道题其实可以用深搜去做,即统计一颗二叉树从根到叶子到底有多少条路径。
来分析一下时间复杂度,这个深搜的算法,其实就是要遍历整个二叉树。
这棵树的深度其实就是m+n-1(深度按从1开始计算)。
那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已)
所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。
动规五部曲
1.确定dp数组以及下标的含义
dp[i][j] :表示从(0,0)出发,到(i, j) 共有dp[i][j]条不同的路径。
2.确定dp数组递推式
因为机器人只能向下或者向右移动,故dp[i][j]是从左边 dp[i][j-1] 或者上边 dp[i-1][j] 的路径叠加而来
故 dp[i][j] = dp[i][j-1] + dp[i-1][j]
3.dp数组初始化
由于机器人只能向下或者向右移动,故 dp[i][0]和 dp[0][j] 都只有一种直走的可能,值都为1
4.确定遍历顺序
由递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 可知,dp[i][j] 都是从其上方和左方推导而来,那么从左到右、从上到下一层一层遍历就能保证每一步都有初值了。
5.手动写几个dp[i][j]推导验证一下

code
class Solution {
public:
int uniquePaths(int m, int n) {
int i=0,j=0;
vector<vector<int>> dp(m,vector<int>(n,0));//m行n列
for(int i=0;i<m;i++)
dp[i][0]=1;
for(int j=0;j<n;j++)
dp[0][j]=1;
for(int i=1;i<m;i++)
for(int j=1;j<n;j++)
dp[i][j]=dp[i][j-1]+dp[i-1][j];
return dp[m-1][n-1];
}
};例题:不同路径Ⅱ
一个机器人位于一个 m x n 网格的左上角 ,
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。

动规五部曲
1.确定dp数组以及下标的含义
dp[i][j] :表示从(0,0)出发,到(i, j) 共有dp[i][j]条不同的路径。
2.确定dp数组递推式
因为机器人只能向下或者向右移动,故dp[i][j]是从左边 dp[i][j-1] 或者上边 dp[i-1][j] 的路径叠加而来
故 dp[i][j]=dp[i][j-1]+dp[i-1][j]
3.dp数组初始化
由于机器人只能向下或者向右移动,且有故障的地方及之后的路是走不到的,故 dp[i][0]和 dp[0][j] 的值都为1,若碰到了故障,之后的值都为0。
4.确定遍历顺序
由递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1可知],dp[i][j]都是从其上方和左方推导而来,那么从左到右、从上到下一层一层遍历就能保证每一步都有初值了。但如果当前的obstacleGrid[i][j]有障碍,那么当前的dp[i][j]赋值为0.
5.手动写几个dp[i][j]推导验证一下
code
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int i=0,j=0;
int m=obstacleGrid.size();
int n=obstacleGrid[0].size();
vector<vector<int>> dp(m,vector<int>(n,0));//m行n列
for(int i=0;i<m;i++)
{
if(obstacleGrid[i][0] == 0)
dp[i][0]=1;
else
break;
}
for(int j=0;j<n;j++)
{
if(obstacleGrid[0][j] == 0)
dp[0][j]=1;
else
break;
}
for(int i=1;i<m;i++)
for(int j=1;j<n;j++)
{
if(obstacleGrid[i][j] != 0)
dp[i][j]=0;
else
dp[i][j]=dp[i][j-1]+dp[i-1][j];
}
return dp[m-1][n-1];
}
};例题:整数拆分
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。

动规五部曲
1.确定dp数组以及下标的含义
dp[i]:拆分数字i,可以得到的最大乘积为dp[i]。
2.确定dp数组递推式
将 i 进行拆分,我们可以选择不拆/拆成2个/拆成多个,再选取最大的数,用递推式表示就是
从1遍历j, dp[i] = max(dp[i], j*(i-j), j*dp[i-j])
j * (i - j) 是单纯的把整数拆分为两个数相乘,而 j * dp[i - j] 是拆分成两个以及两个以上的个数相乘。
3.dp数组初始化
dp[0]=0,dp[1]=0,dp[2]=1
4.确定遍历顺序
从前往后遍历
5.手动写几个dp[i][j]推导验证一下
code:
class Solution {
public:
int integerBreak(int n) {
if(n <= 1) return 0;
vector<int> dp(n+1);
dp[2]=1;
for(int i = 3; i <= n; i++){
for(int j = 1; j < i; j++){
dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j]));
}
}
return dp[n];
}
};例题:不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。

动规五部曲
1.确定dp数组以及下标的含义
dp[i]:由i个整数(从1~i)能构成的二叉搜索书树有dp[i]种。
2.确定dp数组递推式
单纯从dp[i]推出递推式较困难,没什么头绪。于是我们从i为1、2、3等较小的树情况进行推理。
易得,i=1/2/3时情况如下:
i=1:
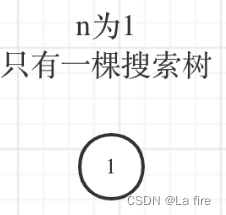
i=2:
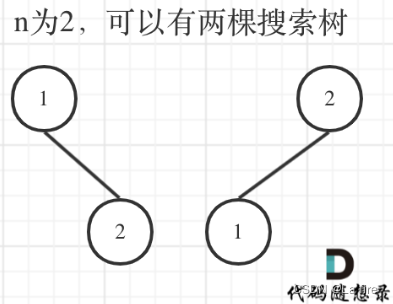
i=3:

可见,i = 3 且根节点为 1 或 3 时,子树结构与 i = 2 时的整棵树结构相似;当根结点为 2 时,其左右子树结构又与 i=1 时的整棵树结构相似。
i=3 且根节点为 1/3 时,二叉搜索树的数量分别为 dp[2] 的值;根节点为 2 时,二叉搜索树的数量为 dp[1] 的值,故 dp[3] = dp[2] + dp[2] + dp[1]。当 i 的数字增加时,二叉树的情况会越来越复杂(可能有2层左子树和1层右子树),所以 dp[3] 的递推式可以看成是 dp[3] = 1*dp[2] + 1*dp[2] + (1或dp[1]) * dp[1],i 值增加时,系数 1 也会发生变化,但我们发现,这3个整式的本质是 左子树的二叉树数量*右子树的二叉树数量 之和。
故我们推测 dp[i] 的递推式为 dp[i] += dp[i-j]*dp[j-1],i-j 的最大值为 i-1,对应的情况是根节点的某一颗子树为空的情况。随着j增大,根节点的两个子树上的结点随之变化。
3.dp数组初始化
易推出 dp[0]=1,dp[1]=1
4.确定遍历顺序
由递推公式可知,dp[i]都是dp[i-j]推导而来的,那么在循环嵌套中先变换j再变换i就能保证dp[i]的来源了。
5.手动写几个dp[i][j]推导验证一下
code
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n+1);
dp[0]=1;;
dp[1]=1;
for(int i=2;i<=n;i++)
for(int j=1;j<=i;j++)
dp[i] += dp[i-j]*dp[j-1];
return dp[n];
}
};

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








