# 创作灵感 #
最近在准备硕博连读考核,写这篇文章是为了巩固基础知识,记录下来我个人不熟悉或者不会的 “知识+题”,筛选掉一下已经很熟悉的基础知识,实现精华内容的提取。
首先指路:数组理论基础 | 代码随想录
估计这篇文章对4年后找工作的我也能有帮助哈哈哈(顺利毕业的话)
注:代码较少,思路为主,适合用于面试的复习【后续会整合更多代码】
目录
1.数组理论基础
需要两点注意的是
- 数组下标都是从0开始的。
- 数组内存空间的地址是连续的
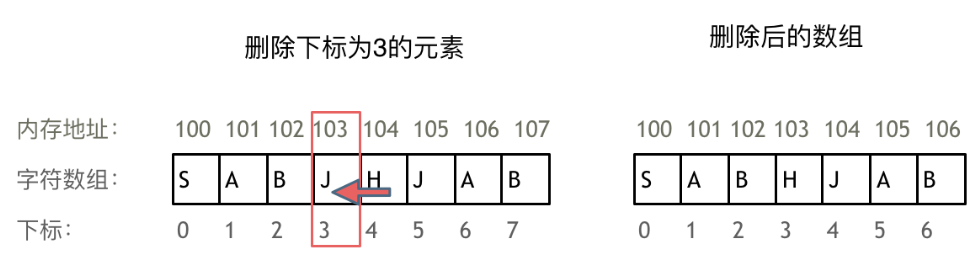
正是因为数组在内存空间的地址是连续的,所以我们在删除或者增添元素的时候,就难免要移动其他元素的地址。
2.二分查找
二分法的前提条件:数组为有序数组、数组中无重复元素
大家写二分法经常写乱,主要是因为对区间的定义没有想清楚,区间的定义就是不变量。要在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,这就是循环不变量规则。
写二分法,区间的定义一般为两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
二分法第一种写法
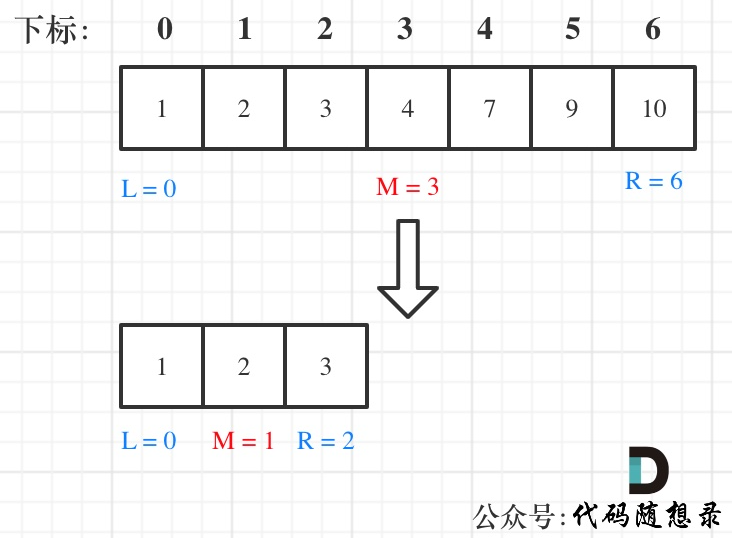
第一种写法,我们定义 target 是在一个在左闭右闭的区间里,也就是[left, right] (这个很重要非常重要)。
区间的定义这就决定了二分法的代码应该如何写,因为定义target在[left, right]区间,所以有如下两点:
- while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
例如在数组:1,2,3,4,7,9,10中查找元素2,如图所示:
- 时间复杂度:O(log n)
- 空间复杂度:O(1)
二分法第二种写法
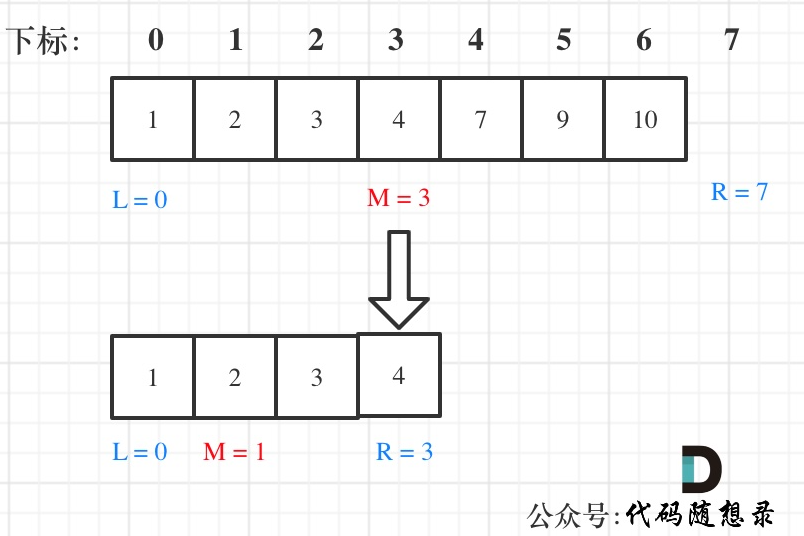
如果说定义 target 是在一个在左闭右开的区间里,也就是[left, right) ,那么二分法的边界处理方式则截然不同。
有如下两点:
- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
在数组:1,2,3,4,7,9,10中查找元素2,如图所示:(注意和方法一的区别)
- 时间复杂度:O(log n)
- 空间复杂度:O(1)
总结
二分法是非常重要的基础算法,为什么很多同学对于二分法都是一看就会,一写就废?
其实主要就是对区间的定义没有理解清楚,在循环中没有始终坚持根据查找区间的定义来做边界处理。
区间的定义就是不变量,那么在循环中坚持根据查找区间的定义来做边界处理,就是循环不变量规则。
本篇根据两种常见的区间定义,给出了两种二分法的写法,每一个边界为什么这么处理,都根据区间的定义做了详细介绍。
3.移除元素
数组的元素在内存地址中是连续的,不能单独删除数组中的某个元素,只能覆盖。
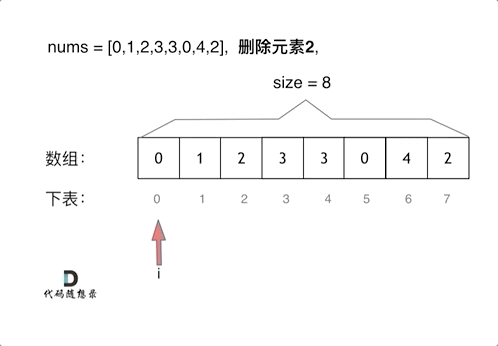
暴力解法
这个题目暴力的解法就是两层for循环,一个for循环遍历数组元素 ,第二个for循环更新数组。
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
双指针法
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
定义快慢指针
- 快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
- 慢指针:指向更新 新数组下标的位置
注意这些实现方法并没有改变元素的相对位置!
- 时间复杂度:O(n)
- 空间复杂度:O(1)
4.有序数组的平方
暴力排序
最直观的想法,莫过于:每个数平方之后,排个序,代码如下:
class Solution {
public:
vector<int> sortedSquares(vector<int>& A) {
for (int i = 0; i < A.size(); i++) {
A[i] *= A[i];
}
sort(A.begin(), A.end()); // 快速排序
return A;
}
};
这个时间复杂度是 O(n + nlogn), 可以说是O(nlogn)的时间复杂度,但为了和下面双指针法算法时间复杂度有鲜明对比,我记为 O(n + nlog n)。
双指针法
数组其实是有序的, 只不过负数平方之后可能成为最大数了。
那么数组平方的最大值就在数组的两端,不是最左边就是最右边,不可能是中间。
此时可以考虑双指针法了,i指向起始位置,j指向终止位置。
定义一个新数组result,和A数组一样的大小,让k指向result数组终止位置。
如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。
如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。
如动画所示:
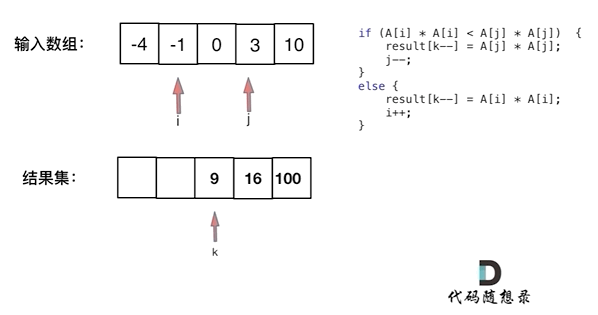
此时的时间复杂度为O(n),相对于暴力排序的解法O(n + nlog n)还是提升不少的。
5.长度最小的子数组
暴力解法
这道题目暴力解法当然是 两个for循环,然后不断的寻找符合条件的子序列,时间复杂度很明显是O(n^2)。
代码如下:
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int result = INT32_MAX; // 最终的结果
int sum = 0; // 子序列的数值之和
int subLength = 0; // 子序列的长度
for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
sum = 0;
for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
sum += nums[j];
if (sum >= s) { // 一旦发现子序列和超过了s,更新result
subLength = j - i + 1; // 取子序列的长度
result = result < subLength ? result : subLength;
break; // 因为我们是找符合条件最短的子序列,所以一旦符合条件就break
}
}
}
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == INT32_MAX ? 0 : result;
}
};
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
后面力扣更新了数据,暴力解法已经超时了。
滑动窗口
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们想要的结果。
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环 完成了一个不断搜索区间的过程。
窗口的起始位置如何移动:如果当前窗口的值大于等于s了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,也就是for循环里的索引。
解题的关键在于 窗口的起始位置如何移动,如图所示:
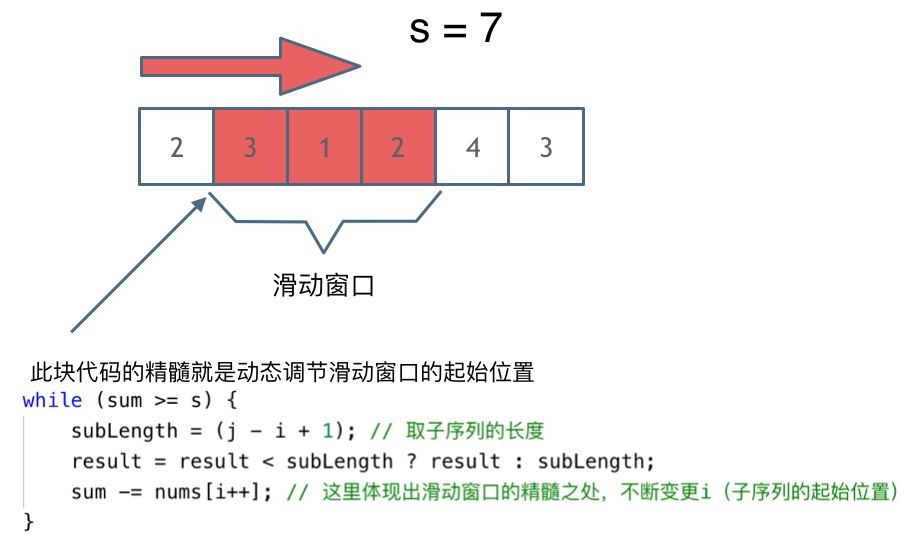
- 时间复杂度:O(n)
- 空间复杂度:O(1)
6.螺旋矩阵
模拟顺时针画矩阵的过程:
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上
按照左闭右开的原则,由外向内一圈一圈这么画下去。
这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
- 时间复杂度 O(n^2): 模拟遍历二维矩阵的时间
- 空间复杂度 O(1)
7.区间和
前缀和 在涉及计算区间和的问题时非常有用!
例如,我们要统计 vec[i] 这个数组上的区间和。
我们先做累加,即 p[i] 表示 下标 0 到 i 的 vec[i] 累加 之和。

如果,我们想统计,在vec数组上 下标 2 到下标 5 之间的累加和,那是不是就用 p[5] - p[1] 就可以了。
为什么呢?
p[1] = vec[0] + vec[1];
p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];
p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];
这不就是我们要求的 下标 2 到下标 5 之间的累加和吗。
特别注意: 在使用前缀和求解的时候,要特别注意 求解区间。
如上图,如果我们要求 区间下标 [2, 5] 的区间和,那么应该是 p[5] - p[1],而不是 p[5] - p[2]。
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, a, b;
cin >> n;
vector<int> vec(n);
vector<int> p(n);
int presum = 0;
for (int i = 0; i < n; i++) {
cin >> vec[i];
presum += vec[i];
p[i] = presum;
}
while (cin >> a >> b) {
int sum;
if (a == 0) sum = p[b];
else sum = p[b] - p[a - 1];
cout << sum << endl;
}
}
8.开发商购买土地
我甚至没看懂题是什么意思....
【题目描述】
在一个城市区域内,被划分成了n * m个连续的区块,每个区块都拥有不同的权值,代表着其土地价值。目前,有两家开发公司,A 公司和 B 公司,希望购买这个城市区域的土地。
现在,需要将这个城市区域的所有区块分配给 A 公司和 B 公司。
然而,由于城市规划的限制,只允许将区域按横向或纵向划分成两个子区域,而且每个子区域都必须包含一个或多个区块。
为了确保公平竞争,你需要找到一种分配方式,使得 A 公司和 B 公司各自的子区域内的土地总价值之差最小。
注意:区块不可再分。
【输入描述】
第一行输入两个正整数,代表 n 和 m。
接下来的 n 行,每行输出 m 个正整数。
输出描述
请输出一个整数,代表两个子区域内土地总价值之间的最小差距。
【输入示例】
3 3 1 2 3 2 1 3 1 2 3
【输出示例】
0
【提示信息】
如果将区域按照如下方式划分:
1 2 | 3 2 1 | 3 1 2 | 3
两个子区域内土地总价值之间的最小差距可以达到 0。
【数据范围】:
- 1 <= n, m <= 100;
- n 和 m 不同时为 1。
思路
看到本题,大家如果想暴力求解,应该是 n^3 的时间复杂度,
一个 for 枚举分割线, 嵌套 两个for 去累加区间里的和。
如果本题要求 任何两个行(或者列)之间的数值总和,大家在0058.区间和 的基础上 应该知道怎么求。
就是前缀和的思路,先统计好,前n行的和 q[n],如果要求矩阵 a行 到 b行 之间的总和,那么就 q[b] - q[a - 1]就好。
至于为什么是 a - 1,大家去看 0058.区间和 的分析,使用 前缀和 要注意 区间左右边的开闭情况。
本题也可以使用 前缀和的思路来求解,先将 行方向,和 列方向的和求出来,这样可以方便知道 划分的两个区间的和。
代码如下:
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main () {
int n, m;
cin >> n >> m;
int sum = 0;
vector<vector<int>> vec(n, vector<int>(m, 0)) ;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> vec[i][j];
sum += vec[i][j];
}
}
// 统计横向
vector<int> horizontal(n, 0);
for (int i = 0; i < n; i++) {
for (int j = 0 ; j < m; j++) {
horizontal[i] += vec[i][j];
}
}
// 统计纵向
vector<int> vertical(m , 0);
for (int j = 0; j < m; j++) {
for (int i = 0 ; i < n; i++) {
vertical[j] += vec[i][j];
}
}
int result = INT_MAX;
int horizontalCut = 0;
for (int i = 0 ; i < n; i++) {
horizontalCut += horizontal[i];
result = min(result, abs(sum - horizontalCut - horizontalCut));
}
int verticalCut = 0;
for (int j = 0; j < m; j++) {
verticalCut += vertical[j];
result = min(result, abs(sum - verticalCut - verticalCut));
}
cout << result << endl;
}
时间复杂度: O(n^2)
其实本题可以在暴力求解的基础上,优化一下,就不用前缀和了,在行向遍历的时候,遇到行末尾就统一一下, 在列向遍历的时候,遇到列末尾就统计一下。
时间复杂度也是 O(n^2)
代码如下:
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main () {
int n, m;
cin >> n >> m;
int sum = 0;
vector<vector<int>> vec(n, vector<int>(m, 0)) ;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> vec[i][j];
sum += vec[i][j];
}
}
int result = INT_MAX;
int count = 0; // 统计遍历过的行
for (int i = 0; i < n; i++) {
for (int j = 0 ; j < m; j++) {
count += vec[i][j];
// 遍历到行末尾时候开始统计
if (j == m - 1) result = min (result, abs(sum - count - count));
}
}
count = 0; // 统计遍历过的列
for (int j = 0; j < m; j++) {
for (int i = 0 ; i < n; i++) {
count += vec[i][j];
// 遍历到列末尾的时候开始统计
if (i == n - 1) result = min (result, abs(sum - count - count));
}
}
cout << result << endl;
}
9.总结
面试中,数组是必考的基础数据结构。
其实数组的题目在思想上一般比较简单的,但是如果想高效,并不容易。
我们之前一共讲解了四道经典数组题目,每一道题目都代表一个类型,一种思想。
#二分法
数组:每次遇到二分法,都是一看就会,一写就废(opens new window)
这道题目呢,考察数组的基本操作,思路很简单,但是通过率在简单题里并不高,不要轻敌。
可以使用暴力解法,通过这道题目,如果追求更优的算法,建议试一试用二分法,来解决这道题目
- 暴力解法时间复杂度:O(n)
- 二分法时间复杂度:O(logn)
在这道题目中我们讲到了循环不变量原则,只有在循环中坚持对区间的定义,才能清楚的把握循环中的各种细节。
二分法是算法面试中的常考题,建议通过这道题目,锻炼自己手撕二分的能力。
#双指针法
双指针法(快慢指针法):通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
- 暴力解法时间复杂度:O(n^2)
- 双指针时间复杂度:O(n)
这道题目迷惑了不少同学,纠结于数组中的元素为什么不能删除,主要是因为以下两点:
- 数组在内存中是连续的地址空间,不能释放单一元素,如果要释放,就是全释放(程序运行结束,回收内存栈空间)。
- C++中vector和array的区别一定要弄清楚,vector的底层实现是array,封装后使用更友好。
双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法。
#滑动窗口
本题介绍了数组操作中的另一个重要思想:滑动窗口。
- 暴力解法时间复杂度:O(n^2)
- 滑动窗口时间复杂度:O(n)
本题中,主要要理解滑动窗口如何移动 窗口起始位置,达到动态更新窗口大小的,从而得出长度最小的符合条件的长度。
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。
如果没有接触过这一类的方法,很难想到类似的解题思路,滑动窗口方法还是很巧妙的。
#模拟行为
模拟类的题目在数组中很常见,不涉及到什么算法,就是单纯的模拟,十分考察大家对代码的掌控能力。
在这道题目中,我们再一次介绍到了循环不变量原则,其实这也是写程序中的重要原则。
相信大家有遇到过这种情况: 感觉题目的边界调节超多,一波接着一波的判断,找边界,拆了东墙补西墙,好不容易运行通过了,代码写的十分冗余,毫无章法,其实真正解决题目的代码都是简洁的,或者有原则性的,大家可以在这道题目中体会到这一点。
#前缀和
代码随想录后续补充题目
前缀和的思路其实很简单,但非常实用,如果没接触过的录友,也很难想到这个解法维度,所以 这是开阔思路 而难度又不高的好题。
#总结
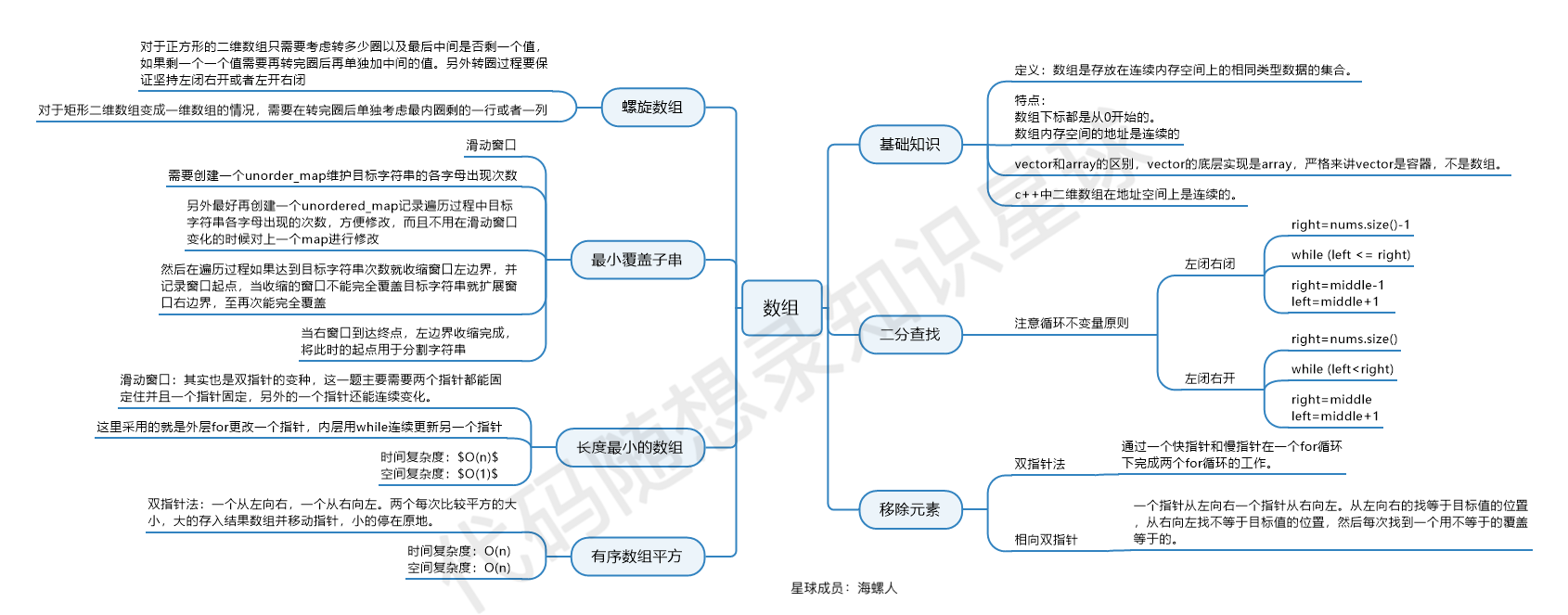
这个图是 代码随想录知识星球 (opens new window)成员:海螺人 (opens new window),所画,总结的非常好,分享给大家。
从二分法到双指针,从滑动窗口到螺旋矩阵,相信如果大家真的认真做了「代码随想录」每日推荐的题目,定会有所收获。
推荐的题目即使大家之前做过了,再读一遍文章,也会帮助你提炼出解题的精髓所在。
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








