# 创作灵感 #
最近在准备硕博连读考核,写这篇文章是为了巩固基础知识,记录下来我个人不熟悉或者不会的 “知识+题”,筛选掉一下已经很熟悉的基础知识,实现精华内容的提取。
首先指路:关于链表,你该了解这些! | 代码随想录
估计这篇文章对4年后找工作的我也能有帮助(顺利毕业的话)
注:代码较少,思路为主,适合用于面试的复习【后续会整合代码】
顺便想感叹一下,本科的时候觉得好难的这些题,现在读研了再回看只能说确实像升级后打第一关一样……
目录
1.链表理论基础
链表的类型
单链表
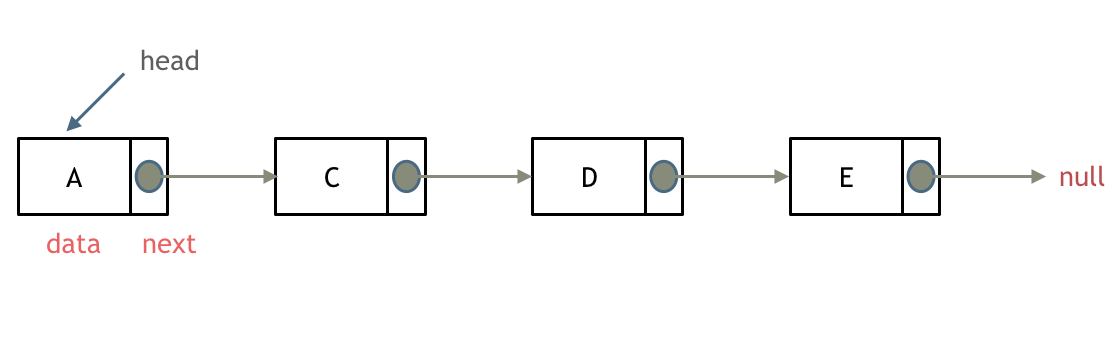
什么是链表,链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,一个是数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(空指针的意思)。
链表的入口节点称为链表的头结点也就是head。
如图所示:
双链表
单链表中的指针域只能指向节点的下一个节点。
双链表:每一个节点有两个指针域,一个指向下一个节点,一个指向上一个节点。
双链表 既可以向前查询也可以向后查询。
循环链表
循环链表,顾名思义,就是链表首尾相连。
循环链表可以用来解决约瑟夫环问题。
链表的存储方式
了解完链表的类型,再来说一说链表在内存中的存储方式。
数组是在内存中是连续分布的,但是链表在内存中可不是连续分布的。
链表是通过指针域的指针链接在内存中各个节点。
所以链表中的节点在内存中不是连续分布的 ,而是散乱分布在内存中的某地址上,分配机制取决于操作系统的内存管理。
如图所示:
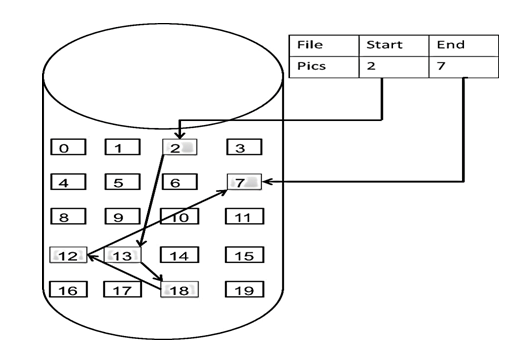
这个链表起始节点为2, 终止节点为7, 各个节点分布在内存的不同地址空间上,通过指针串联在一起。
链表的定义
接下来说一说链表的定义。
链表节点的定义,很多同学在面试的时候都写不好。
这是因为平时在刷leetcode的时候,链表的节点都默认定义好了,直接用就行了,所以同学们都没有注意到链表的节点是如何定义的。
而在面试的时候,一旦要自己手写链表,就写的错漏百出。
这里我给出C/C++的定义链表节点方式,如下所示:
// 单链表
struct ListNode {
int val; // 节点上存储的元素
ListNode *next; // 指向下一个节点的指针
ListNode(int x) : val(x), next(NULL) {} // 节点的构造函数
};
有同学说了,我不定义构造函数行不行,答案是可以的,C++默认生成一个构造函数。
但是这个构造函数不会初始化任何成员变量,下面我来举两个例子:
通过自己定义构造函数初始化节点:
ListNode* head = new ListNode(5);
使用默认构造函数初始化节点:
ListNode* head = new ListNode();
head->val = 5;
所以如果不定义构造函数使用默认构造函数的话,在初始化的时候就不能直接给变量赋值!
链表的操作
删除节点
删除D节点,如图所示:
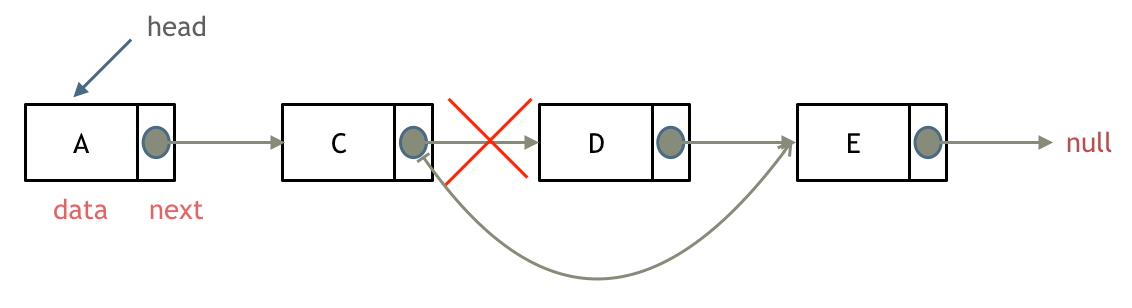
只要将C节点的next指针 指向E节点就可以了。
那有同学说了,D节点不是依然存留在内存里么?只不过是没有在这个链表里而已。
是这样的,所以在C++里最好是再手动释放这个D节点,释放这块内存。
其他语言例如Java、Python,就有自己的内存回收机制,就不用自己手动释放了。
添加节点
如图所示:
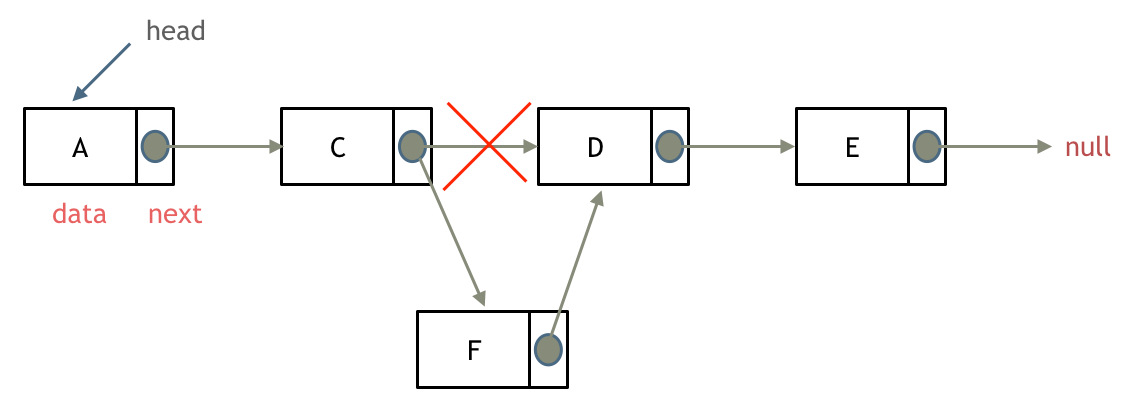
可以看出链表的增添和删除都是O(1)操作,也不会影响到其他节点。
但是要注意,要是删除第五个节点,需要从头节点查找到第四个节点通过next指针进行删除操作,查找的时间复杂度是O(n)。
性能分析
再把链表的特性和数组的特性进行一个对比,如图所示:
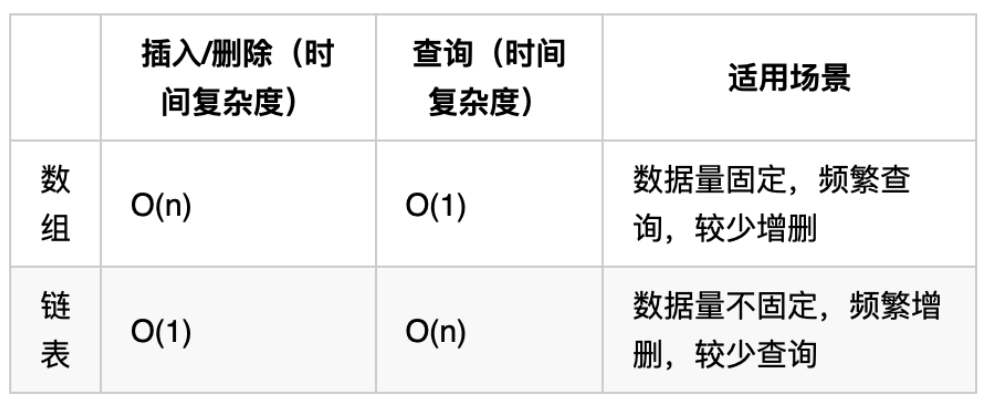
数组在定义的时候,长度就是固定的,如果想改动数组的长度,就需要重新定义一个新的数组。
链表的长度可以是不固定的,并且可以动态增删, 适合数据量不固定,频繁增删,较少查询的场景。
2.移除链表元素
- 直接使用原来的链表来进行删除操作。
- 设置一个虚拟头结点在进行删除操作。
也可以通过递归的思路解决本题:
基础情况:对于空链表,不需要移除元素。
递归情况:首先检查头节点的值是否为 val,如果是则移除头节点,答案即为在头节点的后续节点上递归的结果;如果头节点的值不为 val,则答案为头节点与在头节点的后续节点上递归得到的新链表拼接的结果。
以上三种方法时间复杂度都为 O(n)
3.设计链表
不看了哈,我目前先只看概念,这里都涉及的是代码
4.反转链表
只需要改变链表的next指针的指向,直接将链表反转 ,而不用重新定义一个新的链表,如图所示:
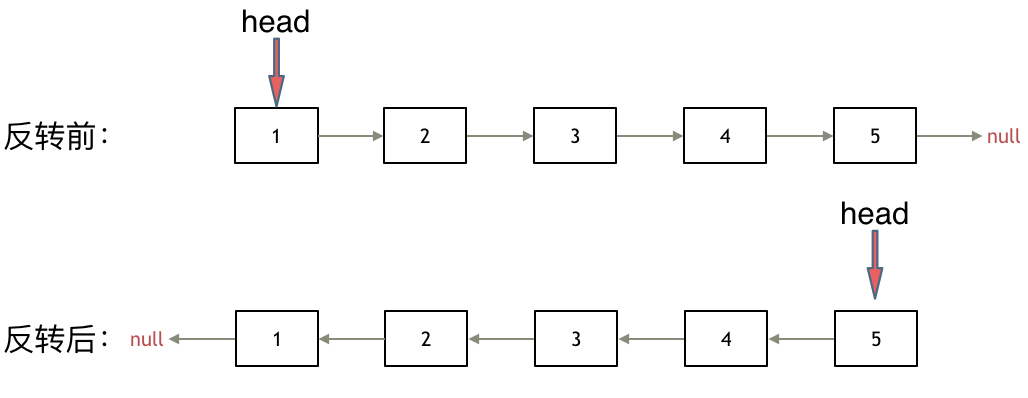
之前链表的头节点是元素1, 反转之后头结点就是元素5 ,这里并没有添加或者删除节点,仅仅是改变next指针的方向。
首先定义一个cur指针,指向头结点,再定义一个pre指针,初始化为null。
然后就要开始反转了,首先要把 cur->next 节点用tmp指针保存一下,也就是保存一下这个节点。
为什么要保存一下这个节点呢,因为接下来要改变 cur->next 的指向了,将cur->next 指向pre ,此时已经反转了第一个节点了。
接下来,就是循环走如下代码逻辑了,继续移动pre和cur指针。
最后,cur 指针已经指向了null,循环结束,链表也反转完毕了。 此时我们return pre指针就可以了,pre指针就指向了新的头结点。
双指针法
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* temp; // 保存cur的下一个节点
ListNode* cur = head;
ListNode* pre = NULL;
while(cur) {
temp = cur->next; // 保存一下 cur的下一个节点,因为接下来要改变cur->next
cur->next = pre; // 翻转操作
// 更新pre 和 cur指针
pre = cur;
cur = temp;
}
return pre;
}
};
- 时间复杂度: O(n)
- 空间复杂度: O(1)
递归法
递归法相对抽象一些,但是其实和双指针法是一样的逻辑,同样是当cur为空的时候循环结束,不断将cur指向pre的过程。
关键是初始化的地方,可能有的同学会不理解, 可以看到双指针法中初始化 cur = head,pre = NULL,在递归法中可以从如下代码看出初始化的逻辑也是一样的,只不过写法变了。
具体可以看代码(已经详细注释),双指针法写出来之后,理解如下递归写法就不难了,代码逻辑都是一样的。
class Solution {
public:
ListNode* reverse(ListNode* pre,ListNode* cur){
if(cur == NULL) return pre;
ListNode* temp = cur->next;
cur->next = pre;
// 可以和双指针法的代码进行对比,如下递归的写法,其实就是做了这两步
// pre = cur;
// cur = temp;
return reverse(cur,temp);
}
ListNode* reverseList(ListNode* head) {
// 和双指针法初始化是一样的逻辑
// ListNode* cur = head;
// ListNode* pre = NULL;
return reverse(NULL, head);
}
};
- 时间复杂度: O(n), 要递归处理链表的每个节点
- 空间复杂度: O(n), 递归调用了 n 层栈空间
我们可以发现,上面的递归写法和双指针法实质上都是从前往后翻转指针指向,其实还有另外一种与双指针法不同思路的递归写法:从后往前翻转指针指向。
具体代码如下(带详细注释):
class Solution {
public:
ListNode* reverseList(ListNode* head) {
// 边缘条件判断
if(head == NULL) return NULL;
if (head->next == NULL) return head;
// 递归调用,翻转第二个节点开始往后的链表
ListNode *last = reverseList(head->next);
// 翻转头节点与第二个节点的指向
head->next->next = head;
// 此时的 head 节点为尾节点,next 需要指向 NULL
head->next = NULL;
return last;
}
};
- 时间复杂度: O(n)
- 空间复杂度: O(n)
5.两两交换链表中的节点
建议使用虚拟头结点,这样会方便很多,要不然每次针对头结点(没有前一个指针指向头结点),还要单独处理。
对虚拟头结点的操作,还不熟悉的话,可以看这篇链表:听说用虚拟头节点会方便很多? (opens new window)。
接下来就是交换相邻两个元素了,此时一定要画图,不画图,操作多个指针很容易乱,而且要操作的先后顺序
初始时,cur指向虚拟头结点,然后进行如下三步:
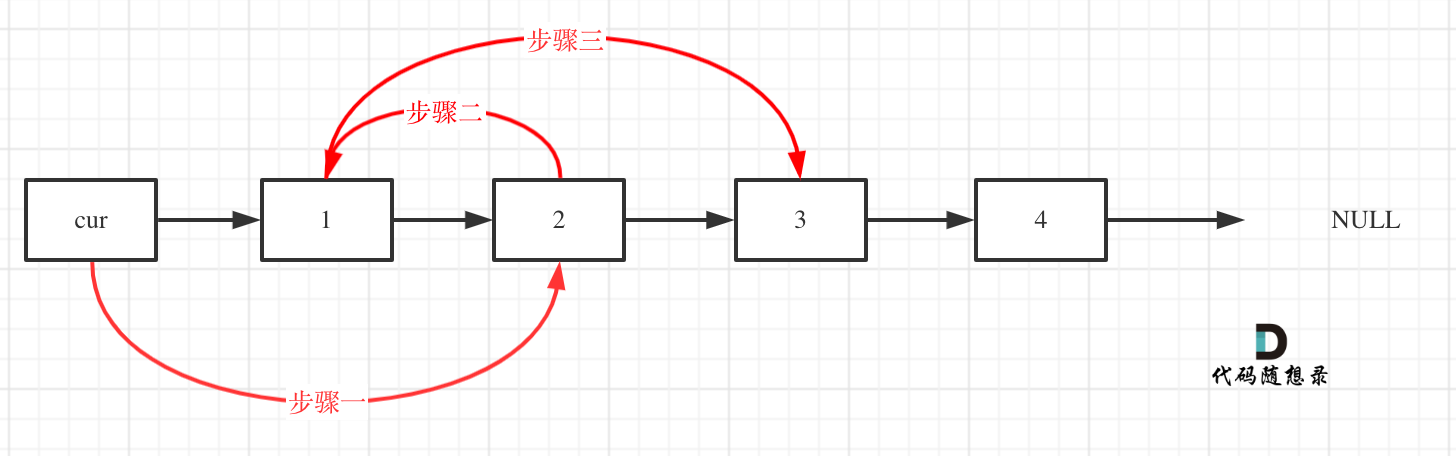
看这个可能就更直观一些了:
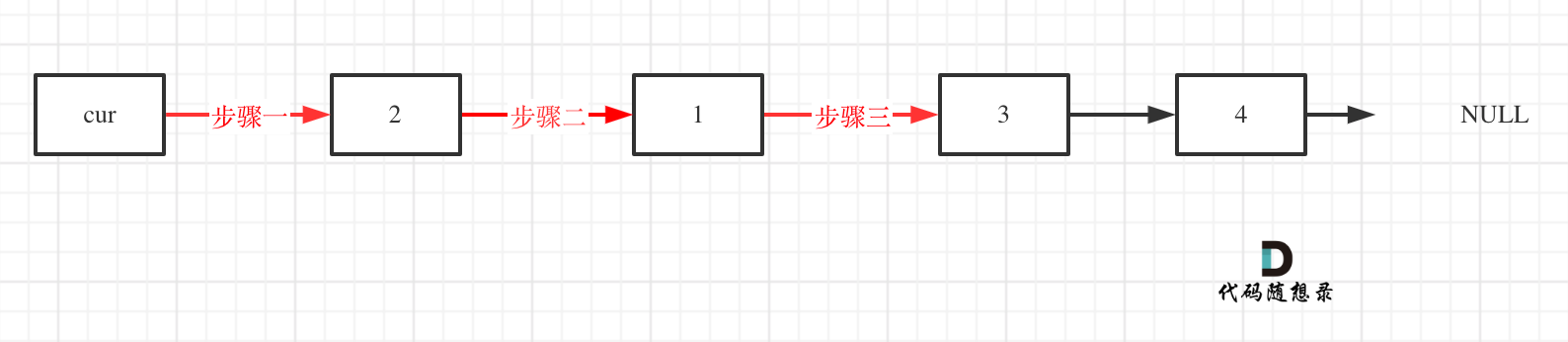
对应的C++代码实现如下: (注释中详细和如上图中的三步做对应)
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
dummyHead->next = head; // 将虚拟头结点指向head,这样方便后面做删除操作
ListNode* cur = dummyHead;
while(cur->next != nullptr && cur->next->next != nullptr) {
ListNode* tmp = cur->next; // 记录临时节点
ListNode* tmp1 = cur->next->next->next; // 记录临时节点
cur->next = cur->next->next; // 步骤一
cur->next->next = tmp; // 步骤二
cur->next->next->next = tmp1; // 步骤三
cur = cur->next->next; // cur移动两位,准备下一轮交换
}
ListNode* result = dummyHead->next;
delete dummyHead;
return result;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
6.删除链表的倒数第N个节点
双指针的经典应用,如果要删除倒数第n个节点,让fast移动n步,然后让fast和slow同时移动,直到fast指向链表末尾。删掉slow所指向的节点就可以了。
思路是这样的,但要注意一些细节。
分为如下几步:
-
首先这里我推荐大家使用虚拟头结点,这样方便处理删除实际头结点的逻辑,如果虚拟头结点不清楚,可以看这篇: 链表:听说用虚拟头节点会方便很多?(opens new window)
-
定义fast指针和slow指针,初始值为虚拟头结点,如图:
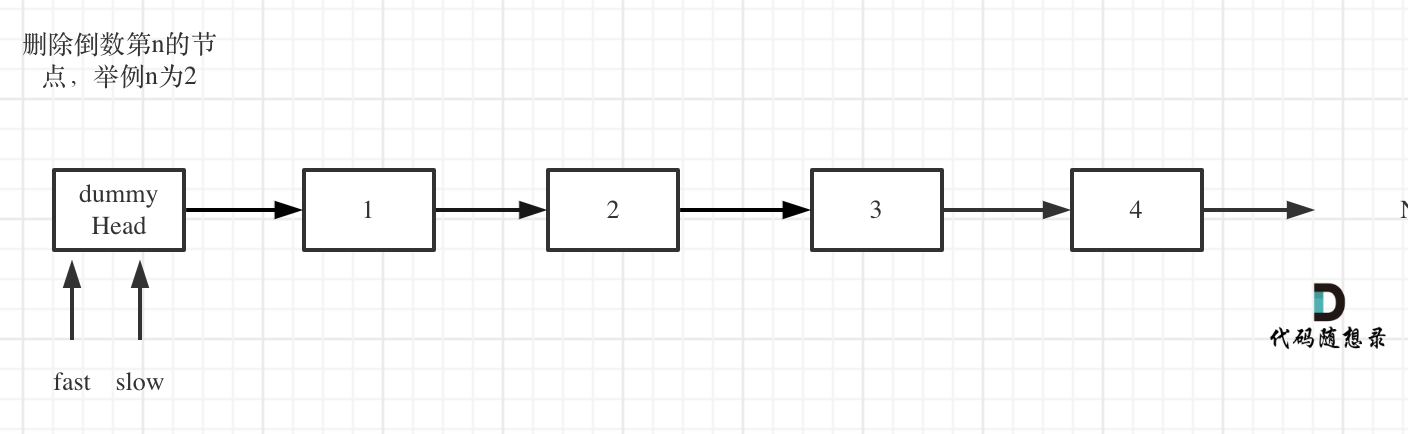
-
fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
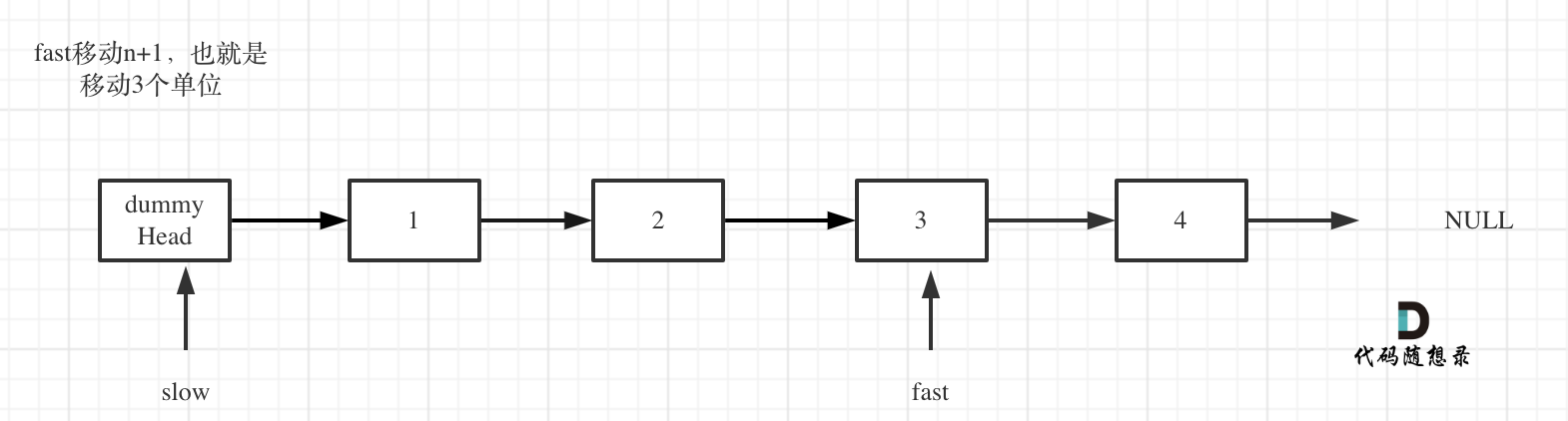
-
fast和slow同时移动,直到fast指向末尾,如题:
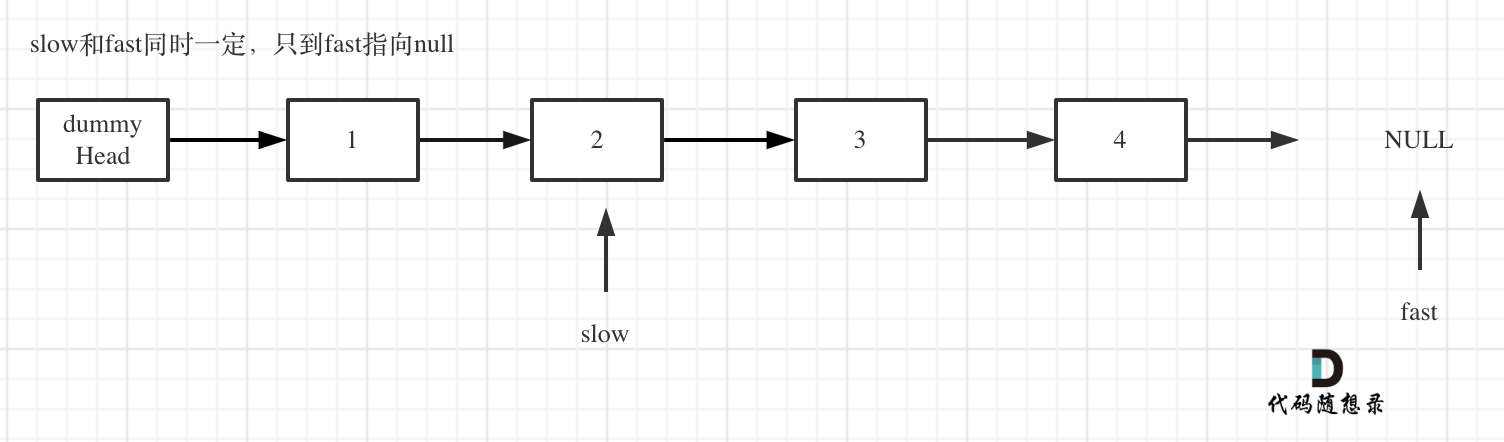
//图片中有错别词:应该将“只到”改为“直到”
-
删除slow指向的下一个节点,如图:
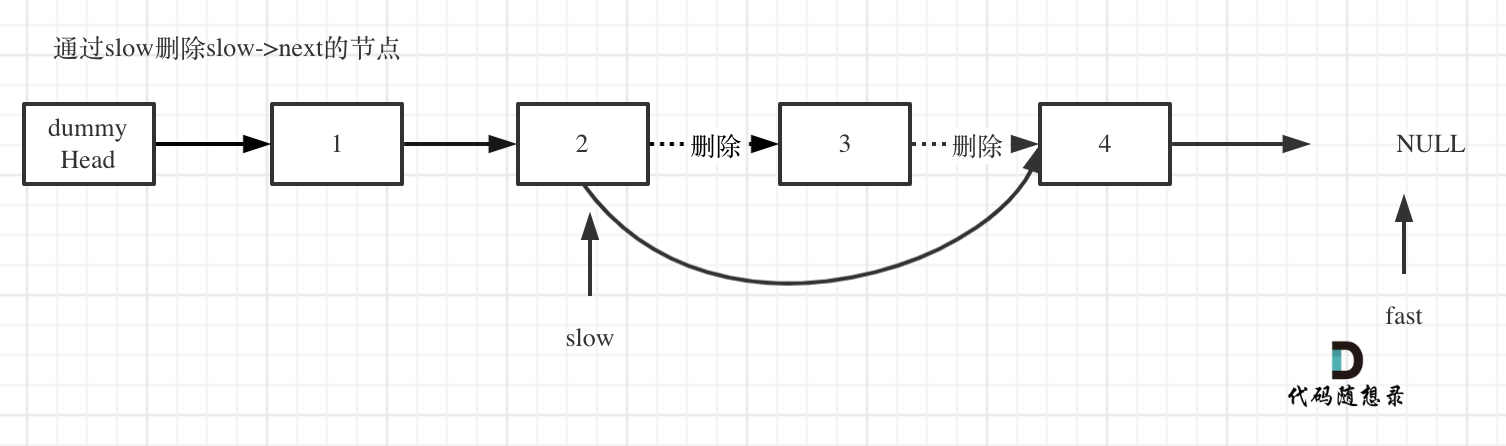
此时不难写出如下C++代码:
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
ListNode* slow = dummyHead;
ListNode* fast = dummyHead;
while(n-- && fast != NULL) {
fast = fast->next;
}
fast = fast->next; // fast再提前走一步,因为需要让slow指向删除节点的上一个节点
while (fast != NULL) {
fast = fast->next;
slow = slow->next;
}
slow->next = slow->next->next;
// ListNode *tmp = slow->next; C++释放内存的逻辑
// slow->next = tmp->next;
// delete tmp;
return dummyHead->next;
}
};
- 时间复杂度: O(n)
- 空间复杂度: O(1)
7.链表相交
简单来说,就是求两个链表交点节点的指针。 这里同学们要注意,交点不是数值相等,而是指针相等。
为了方便举例,假设节点元素数值相等,则节点指针相等。
看如下两个链表,目前curA指向链表A的头结点,curB指向链表B的头结点:
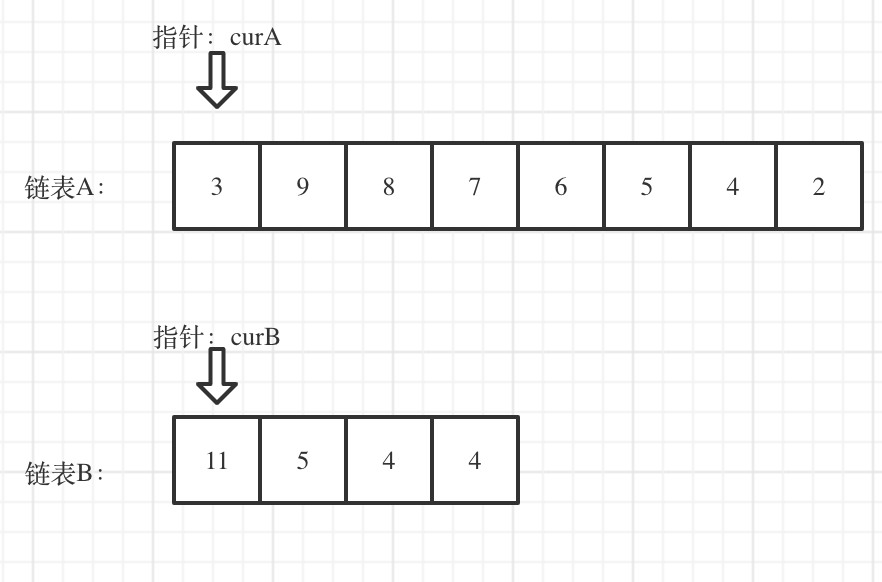
我们求出两个链表的长度,并求出两个链表长度的差值,然后让curA移动到,和curB 末尾对齐的位置,如图:
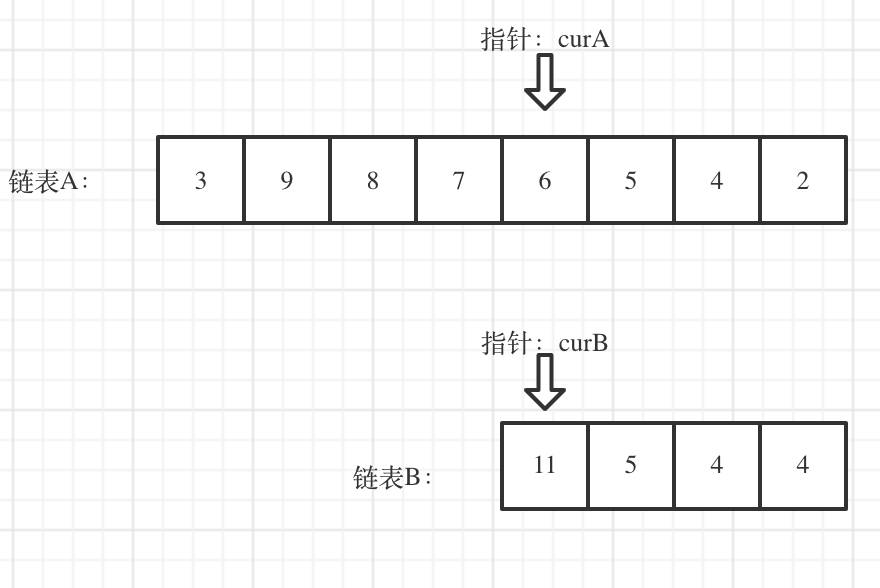
此时我们就可以比较curA和curB是否相同,如果不相同,同时向后移动curA和curB,如果遇到curA == curB,则找到交点。
否则循环退出返回空指针。
C++代码如下:
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* curA = headA;
ListNode* curB = headB;
int lenA = 0, lenB = 0;
while (curA != NULL) { // 求链表A的长度
lenA++;
curA = curA->next;
}
while (curB != NULL) { // 求链表B的长度
lenB++;
curB = curB->next;
}
curA = headA;
curB = headB;
// 让curA为最长链表的头,lenA为其长度
if (lenB > lenA) {
swap (lenA, lenB);
swap (curA, curB);
}
// 求长度差
int gap = lenA - lenB;
// 让curA和curB在同一起点上(末尾位置对齐)
while (gap--) {
curA = curA->next;
}
// 遍历curA 和 curB,遇到相同则直接返回
while (curA != NULL) {
if (curA == curB) {
return curA;
}
curA = curA->next;
curB = curB->next;
}
return NULL;
}
};
- 时间复杂度:O(n + m)
- 空间复杂度:O(1)
8.环形链表
这道题目,不仅考察对链表的操作,而且还需要一些数学运算。
主要考察两知识点:
- 判断链表是否环
- 如果有环,如何找到这个环的入口
#判断链表是否有环
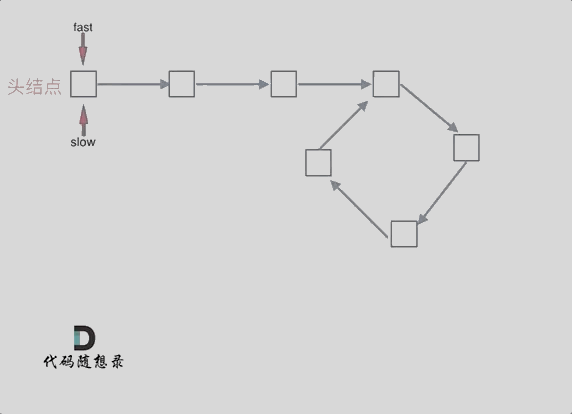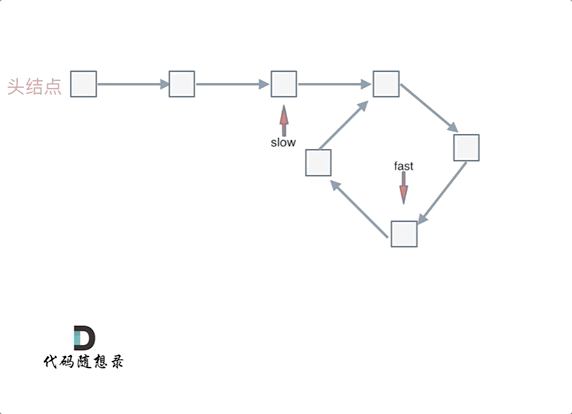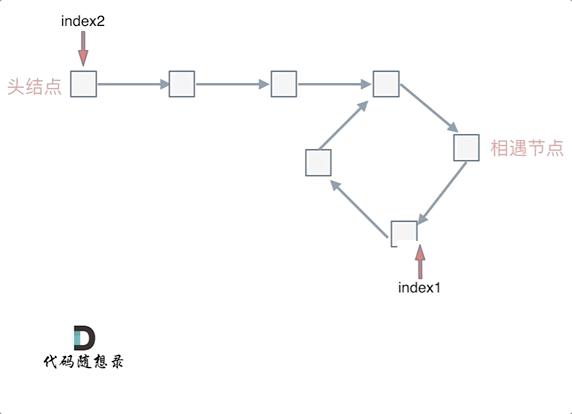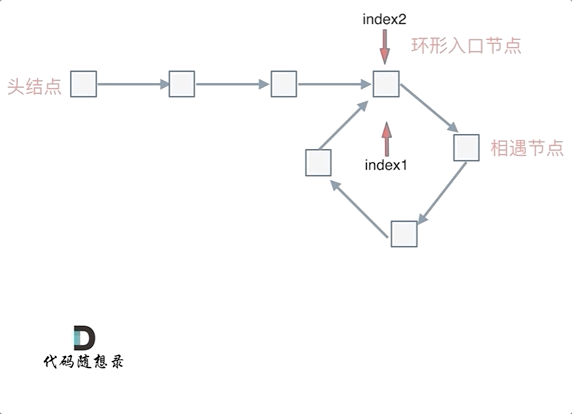
可以使用快慢指针法,分别定义 fast 和 slow 指针,从头结点出发,fast指针每次移动两个节点,slow指针每次移动一个节点,如果 fast 和 slow指针在途中相遇 ,说明这个链表有环。
为什么fast 走两个节点,slow走一个节点,有环的话,一定会在环内相遇呢,而不是永远的错开呢
首先第一点:fast指针一定先进入环中,如果fast指针和slow指针相遇的话,一定是在环中相遇,这是毋庸置疑的。
那么来看一下,为什么fast指针和slow指针一定会相遇呢?
可以画一个环,然后让 fast指针在任意一个节点开始追赶slow指针。
会发现最终都是这种情况, 如下图:
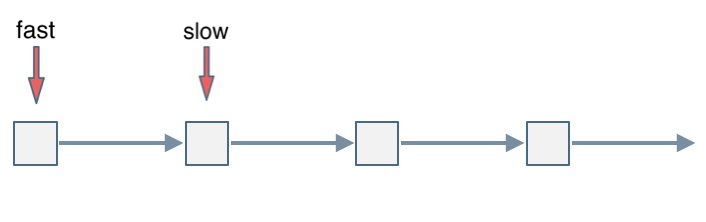
fast和slow各自再走一步, fast和slow就相遇了
这是因为fast是走两步,slow是走一步,其实相对于slow来说,fast是一个节点一个节点的靠近slow的,所以fast一定可以和slow重合。
动画如下:
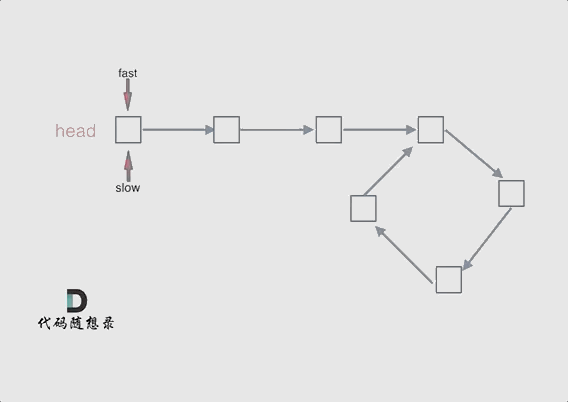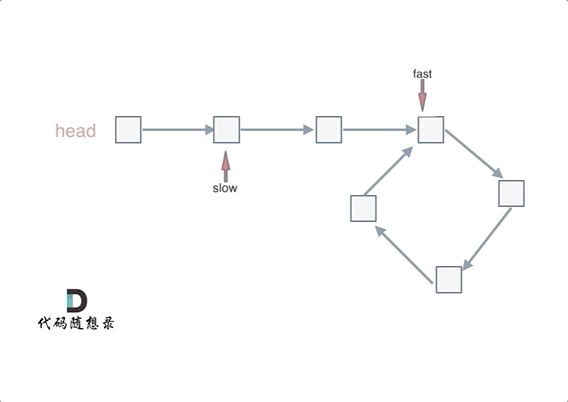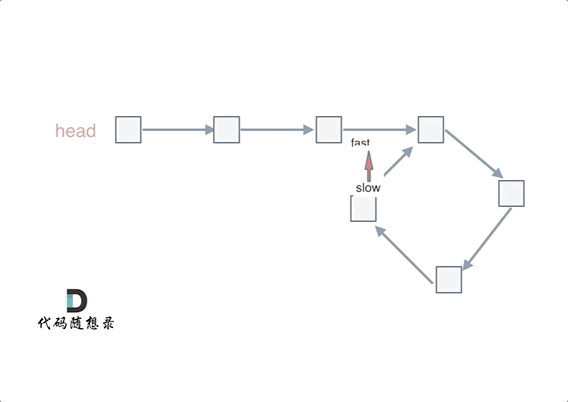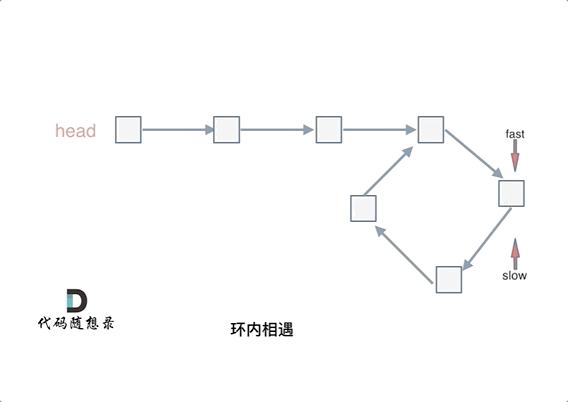
#如果有环,如何找到这个环的入口
此时已经可以判断链表是否有环了,那么接下来要找这个环的入口了。
假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示:
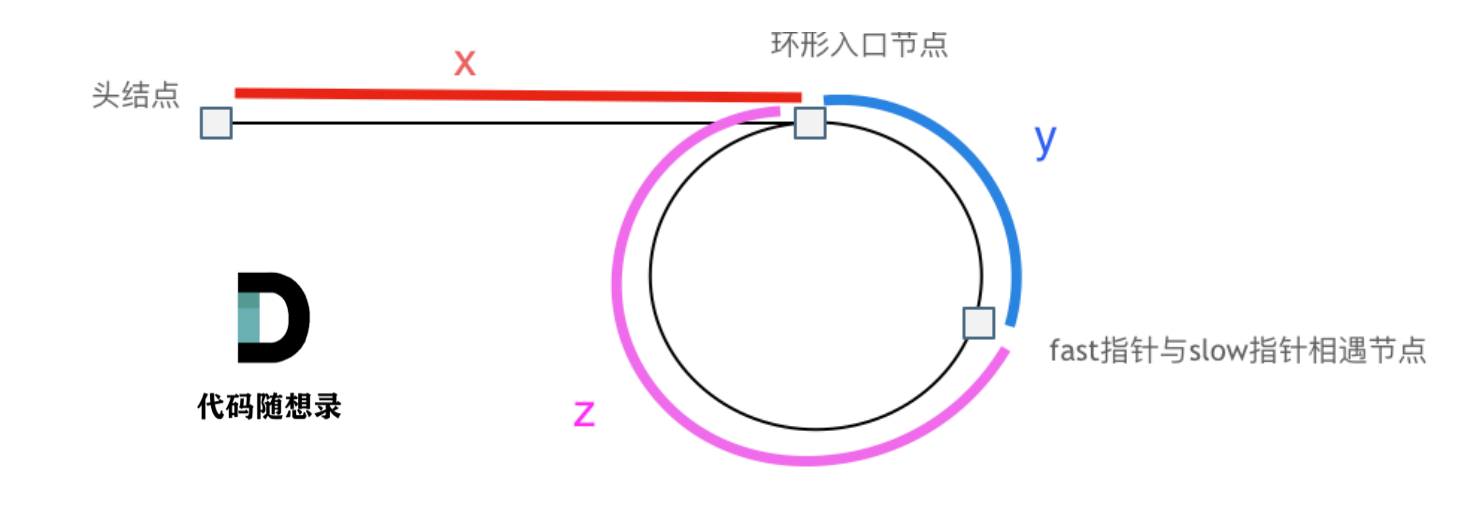
那么相遇时: slow指针走过的节点数为: x + y, fast指针走过的节点数:x + y + n (y + z),n为fast指针在环内走了n圈才遇到slow指针, (y+z)为 一圈内节点的个数A。
因为fast指针是一步走两个节点,slow指针一步走一个节点, 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2:
(x + y) * 2 = x + y + n (y + z)
两边消掉一个(x+y): x + y = n (y + z)
因为要找环形的入口,那么要求的是x,因为x表示 头结点到 环形入口节点的的距离。
所以要求x ,将x单独放在左面:x = n (y + z) - y ,
再从n(y+z)中提出一个 (y+z)来,整理公式之后为如下公式:x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的,因为 fast指针至少要多走一圈才能相遇slow指针。
这个公式说明什么呢?
先拿n为1的情况来举例,意味着fast指针在环形里转了一圈之后,就遇到了 slow指针了。
当 n为1的时候,公式就化解为 x = z,
这就意味着,从头结点出发一个指针,从相遇节点 也出发一个指针,这两个指针每次只走一个节点, 那么当这两个指针相遇的时候就是 环形入口的节点。
也就是在相遇节点处,定义一个指针index1,在头结点处定一个指针index2。
让index1和index2同时移动,每次移动一个节点, 那么他们相遇的地方就是 环形入口的节点。
动画如下:
那么 n如果大于1是什么情况呢,就是fast指针在环形转n圈之后才遇到 slow指针。
其实这种情况和n为1的时候 效果是一样的,一样可以通过这个方法找到 环形的入口节点,只不过,index1 指针在环里 多转了(n-1)圈,然后再遇到index2,相遇点依然是环形的入口节点。
代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
while(fast != NULL && fast->next != NULL) {
slow = slow->next;
fast = fast->next->next;
// 快慢指针相遇,此时从head 和 相遇点,同时查找直至相遇
if (slow == fast) {
ListNode* index1 = fast;
ListNode* index2 = head;
while (index1 != index2) {
index1 = index1->next;
index2 = index2->next;
}
return index2; // 返回环的入口
}
}
return NULL;
}
};
- 时间复杂度: O(n),快慢指针相遇前,指针走的次数小于链表长度,快慢指针相遇后,两个index指针走的次数也小于链表长度,总体为走的次数小于 2n
- 空间复杂度: O(1)
9.总结
链表的理论基础
在这篇文章关于链表,你该了解这些! (opens new window)中,介绍了如下几点:
- 链表的种类主要为:单链表,双链表,循环链表
- 链表的存储方式:链表的节点在内存中是分散存储的,通过指针连在一起。
- 链表是如何进行增删改查的。
- 数组和链表在不同场景下的性能分析。
可以说把链表基础的知识都概括了,但又不像教科书那样的繁琐。
链表经典题目
#虚拟头结点
在链表:听说用虚拟头节点会方便很多? (opens new window)中,我们讲解了链表操作中一个非常重要的技巧:虚拟头节点。
链表的一大问题就是操作当前节点必须要找前一个节点才能操作。这就造成了,头结点的尴尬,因为头结点没有前一个节点了。
每次对应头结点的情况都要单独处理,所以使用虚拟头结点的技巧,就可以解决这个问题。
在链表:听说用虚拟头节点会方便很多? (opens new window)中,我给出了用虚拟头结点和没用虚拟头结点的代码,大家对比一下就会发现,使用虚拟头结点的好处。
#链表的基本操作
在链表:一道题目考察了常见的五个操作! (opens new window)中,我们通过设计链表把链表常见的五个操作练习了一遍。
这是练习链表基础操作的非常好的一道题目,考察了:
- 获取链表第index个节点的数值
- 在链表的最前面插入一个节点
- 在链表的最后面插入一个节点
- 在链表第index个节点前面插入一个节点
- 删除链表的第index个节点的数值
可以说把这道题目做了,链表基本操作就OK了,再也不用担心链表增删改查整不明白了。
这里我依然使用了虚拟头结点的技巧,大家复习的时候,可以去看一下代码。
#反转链表
在链表:听说过两天反转链表又写不出来了? (opens new window)中,讲解了如何反转链表。
因为反转链表的代码相对简单,有的同学可能直接背下来了,但一写还是容易出问题。
反转链表是面试中高频题目,很考察面试者对链表操作的熟练程度。
我在文章 (opens new window)中,给出了两种反转的方式,迭代法和递归法。
建议大家先学透迭代法,然后再看递归法,因为递归法比较绕,如果迭代还写不明白,递归基本也写不明白了。
可以先通过迭代法,彻底弄清楚链表反转的过程!
#删除倒数第N个节点
在链表:删除链表倒数第N个节点,怎么删? (opens new window)中我们结合虚拟头结点 和 双指针法来移除链表倒数第N个节点。
#链表相交
链表:链表相交 (opens new window)使用双指针来找到两个链表的交点(引用完全相同,即:内存地址完全相同的交点)
#环形链表
在链表:环找到了,那入口呢? (opens new window)中,讲解了在链表如何找环,以及如何找环的入口位置。
这道题目可以说是链表的比较难的题目了。 但代码却十分简洁,主要在于一些数学证明。
总结
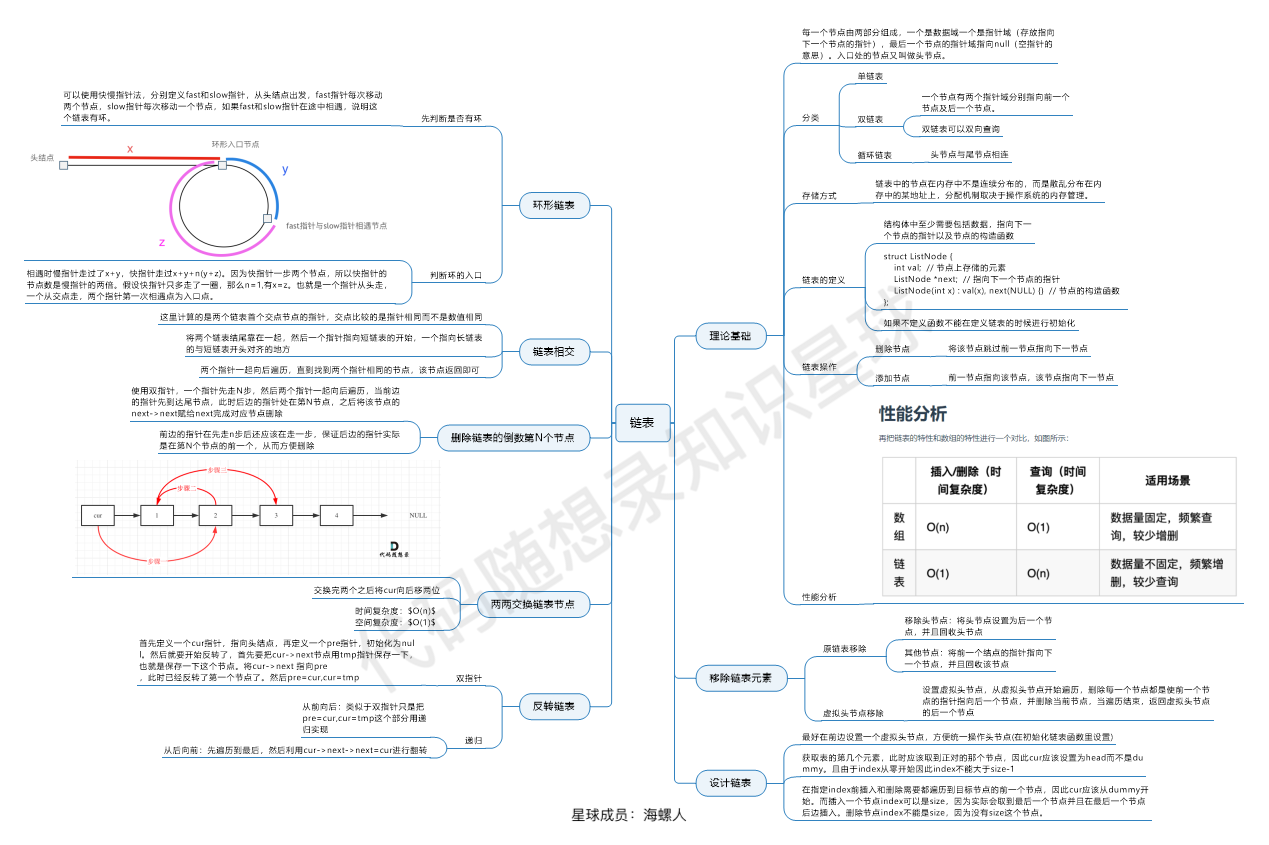
这个图是 代码随想录知识星球 (opens new window)成员:海螺人 (opens new window),所画,总结的非常好,分享给大家。
考察链表的操作其实就是考察指针的操作,是面试中的常见类型。
链表篇中开头介绍链表理论知识 (opens new window),然后分别通过经典题目介绍了如下知识点:
























 8289
8289

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








