题面:
# P10789 [NOI2024] 登山
## 题目描述
“为什么要攀登?因为山就在那里。”
慕士塔格山上有 $n$ 处点位,点从 $1$ 到 $n$ 编号,$1$ 号点位为山顶。这 $n$ 个点位构成一棵有根树的结构,其中 $1$ 号点位为根,对于 $2\leq i\leq n$,$i$ 号点位的父亲结点为 $p_i$ 号点位。
记 $d_i$ 为 $i$ 号点位到山顶所需经过的边数。形式化地说,$d_1=0$,对于 $2\leq i\leq n$,$d_i=d_{p_i}+1$。
定义一条**登山路径**为从 $2\sim n$ 号点位中的某一个开始,经过若干次**移动**后**到达山顶**的方案。
定义一次从 $i(2\leq i\leq n)$ 号点位出发的**移动**为以下两种方式之一:
1. 冲刺:在给定的冲刺范围 $[l_i,r_i]$ 内,选择一个正整数 $k$ 满足 $l_i\leq k\leq r_i$,向山顶移动 $k$ 步,即移动至 $i$ 号点位在有根树上的 $k$ 级父亲处。保证 $1\leq l_i\leq r_i\leq d_i$。
2. 休息:由于慕士塔格山地形陡峭,休息时会滑落到某一个儿子结点处。形式化地说,选择一个满足 $p_j=i$ 的 $j$,移动至到 $j$ 号点位。特别地,若 $i$ 号点位为有根树的叶子结点,则不存在满足 $p_j=i$ 的 $j$,因此此时不能选择休息。
定义一条**登山路径**对应的**登山序列**为初始点位以及每次移动到的点位所构成的序列。形式化地说,一条从 $x$ 号点位开始的**登山路径**对应的****登山序列****是一个点序列 $a_1=x,a_2,\dots,a_m=1$ 满足对于 $1\leq i<m$,$a_{i+1}$ 是 $a_i$ 的 $k(l_{a_i}\leq k\leq r_{a_i})$ 级祖先或 $p_{a_{i+1}}=a_i$。
为了保证每次冲刺都能更接近山顶,一条**合法的登山路径**需要满足:对于初始点位或某次移动到的点位 $i$,以后冲刺到的点位 $j$ 都必须满足 $d_j<d_i-h_i$,其中 $h_i$ 是一个给定的参数,保证 $0\leq h_i<d_i$。形式化地说,一条**合法的登山路径**对应的**登山序列** $a_1,a_2,\dots,a_m$ 需要满足:对于所有 $1\leq i<j\leq m$,若 $p_{a_j} \neq a_{j-1}$,则 $d_{a_j}<d_{a_i}-h_{a_i}$。
对于 $2\sim n$ 号所有点位,求从这些点位开始的**合法的登山路径**条数。两条**登山路径**不同当且仅当其对应的**登山序列**不同。由于答案可能较大,你只需要求出答案对 $998\,244\,353$ 取模后的结果。
## 输入格式
**本题有多组测试数据。**
输入的第一行包含一个整数 $c$,表示测试点编号。$c=0$ 表示该测试点为样例。
输入的第二行包含一个整数 $t$,表示测试数据组数。
接下来依次输入每组测试数据,对于每组测试数据:
输入的第一行包含一个整数 $n$,表示慕士塔格山的点位数量。
接下来 $n-1$ 行,第 $i-1(2\leq i\leq n)$ 行包含四个整数 $p_i,l_i,r_i,h_i$。保证 $1\leq p_i<i$,$1\leq l_i\leq r_i\leq d_i$,$0\leq h_i<d_i$。
## 输出格式
对于每组测试数据,输出一行 $n-1$ 个整数,分别表示从点位 $2\sim n$ 到达山顶的方案数对 $998\,244\,353$ 取模后的结果。
## 输入输出样例 #1
### 输入 #1
```
0
3
5
1 1 1 0
2 1 1 0
2 1 2 1
4 2 3 0
6
1 1 1 0
2 1 2 0
3 1 3 2
4 1 4 1
5 1 5 3
6
1 1 1 0
2 1 2 0
2 1 2 0
3 1 2 0
3 2 3 2
```
### 输出 #1
```
3 3 2 4
5 9 3 21 6
4 10 5 14 1
```
## 输入输出样例 #2
### 输入 #2
```
见 mountain2.in/ans
这个样例满足测试点 2,3 的约束条件
```
### 输出 #2
```
```
## 输入输出样例 #3
### 输入 #3
```
见 mountain3.in/ans
这个样例满足测试点 9 的约束条件
```
### 输出 #3
```
```
## 输入输出样例 #4
### 输入 #4
```
见 mountain4.in/ans
这个样例满足测试点 11,12 的约束条件
```
### 输出 #4
```
```
## 输入输出样例 #5
### 输入 #5
```
见 mountain5.in/ans
这个样例满足测试点 13 的约束条件
```
### 输出 #5
```
```
## 说明/提示
**【样例 1 解释】**
样例 $1$ 共包含三组测试数据。
对于第一组测试数据,慕士塔格山的点位结构如下:
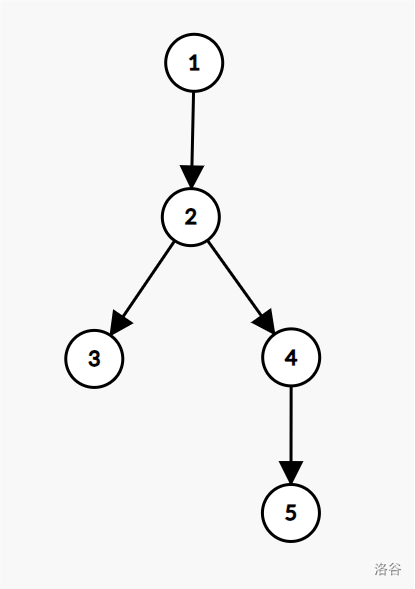
在该测试数据中,$d_1=0$,$d_2=1$,$d_3=d_4=2$,$d_5=3$。
从 $4$ 开始的合法的登山路径共有以下 $2$ 条:
1. 直接选择冲刺到 $4$ 的 $2$ 级父亲,也就是 $1$,到达山顶,对应的登山序列为 $[4,1]$。
2. 先休息滑落到 $5$,然后从 $5$ 冲刺到它的 $3$ 级父亲,到达山顶。对应的登山序列为 $[4,5,1]$。
从 $5$ 开始的合法的登山路径共有以下 $4$ 条:
1. 直接选择冲刺到 $5$ 的 $3$ 级父亲,也就是 $1$,到达山顶。对应的登山序列为 $[5,1]$。
2. 先冲刺到 $5$ 的 $2$ 级父亲,也就是 $2$;然后再从 $2$ 冲刺到它的 $1$ 级父亲,到达山顶。对应的登山序列为 $[5,2,1]$。
3. 先冲刺到 $5$ 的 $2$ 级父亲,也就是 $2$;然后在 $2$ 处休息,滑落到 $4$;接着从 $4$ 冲刺到它的 $2$ 级父亲,到达山顶。对应的登山序列为 $[5,2,4,1]$。
4. 先冲刺到 $5$ 的 $2$ 级父亲,也就是 $2$;然后在 $2$ 处休息,滑落到 $4$;继续休息,滑落到 $5$;接着从 $5$ 再次冲刺到它的 $3$ 级父亲,到达山顶。对应的登山序列为 $[5,2,4,5,1]$。
**【数据范围】**
对于所有测试数据保证:$1\leq t\leq 4$,$2\leq n\leq 10^5$。
对于任意的 $2\leq i\leq n$,保证:$1\leq p_i<i$,$1\leq l_i\leq r_i\leq d_i$,$0\leq h_i<d_i$。
| 测试点编号 | $n\leq$ | 是否有 $l_i=r_i$ | 是否有 $h_i=0$ | 是否有 $p_i=i-1$ |
| :----------: | :----------: | :----------: | :----------: | :----------: |
| $1$ | $6$ | 否 | 否 | 否 |
| $2,3$ | $300$ | 否 | 否 | 否 |
| $4,5$ | $5000$ | 否 | 否 | 否 |
| $6$ | $10^5$ | 是 | 是 | 是 |
| $7$ | $10^5$ | 是 | 是 | 否 |
| $8$ | $10^5$ | 是 | 否 | 是 |
| $9$ | $10^5$ | 是 | 否 | 否 |
| $10$ | $10^5$ | 否 | 是 | 是 |
| $11,12$ | $10^5$ | 否 | 是 | 否 |
| $13$ | $10^5$ | 否 | 否 | 是 |
| $14\sim 20$ | $10^5$ | 否 | 否 | 否 |
题解:
显然要考虑 dp,最终需要求出的是 $f_i$ 表示 $i\to 1$ 的方案数,初始有 $f_1=1$。方便起见,令 $h_u$ 的值表示 $d_u-h'_u-1$,$h'$ 是题面中读入的原始值。转移只需要考虑对第一次向上冲刺的位置进行转移,枚举 $u$ 子树中的点 $v$ 表示向下 $u$ 休息到了 $v$,枚举 $u$ 的祖先之一 $i$,如果满足 $d_v-d_i\in[l_v,r_v]$ 且 $d_i\leq \min_{j\in\text{path}(u,v)}h_j$ 就需要有 $f_i$ 转移到 $f_u$,不难通过枚举 $v$ 并处理前缀和做到 $\mathcal O(n^2)$。
可以感受到,正解是几乎在线的数据结构优化问题,问题在于维护出所有 $f_i$ 的系数 $coef_i$ 使得 $f_u=\sum coef_if_i$。其中 $coef_i$ 的意义就表示 $u$ 子树有多少个 $v$ 使得 $f_i\to f_u$ 的转移是合法的。那么子树中 $l_v,r_v$ 就相当于链 $+1$,但是 $h$ 让问题复杂了起来。为了去掉与区间 $[l,r]$ 的交集,我们尝试将更新改为对于 $r_v+1$ 以上的 $coef$ 进行 $-1$,对于 $l_v$ 以上的进行 $+1$;$h$ 的限制对两个操作独立,分别是 $+1$ 和 $-1$。具体的,我们考虑 $u\to1$ 的链,从前往后是深度为 $0,1,\cdots,d_u$ 的点,构成一个长度为 $d_u+1$ 的序列 $s$,$s$ 序列的每个元素是 $h_i$,由不同的 $R\in\text{anc}(u)$ 表示当前考虑到 $f_R$,就会有不同的区间的 $coef$ 被重置为 $0$。先考虑这个序列 $s$,一个结论是我们只会关心所有的后缀最小值位置集合 $P$,当找到 $R$ 时,我们只关心 $R$ 在这个序列中向后大于等于它的首个 $P$ 中的元素,因此我们可以构造一个重构树,$u$ 的父亲 $up_u$ 表示 $u$ 的祖先中最深的 $v$ 使得 $h_v<h_u$,显然这相当于跳了若干级祖先,重构树上的边代表着原树的一条直链,更新理应是链加。对于这两个限制可以分开考虑,不妨看到 $[0,p]$ 的操作 $+1$,那么对于某个 $u$ 其造成的就是 $[h_{\text{next}_u}+1,p]$。所以我们可以找到 $P$ 中首个 $h<p$ 的位置打上 $[h+1,p]$ 的标记,后续的 $\min$ 更新操作就与 $p$ 无关了,给 $h$ 打一个 tag 然后在重构树 dfs 时累加一下这个标记即可。后续的颜色视为 $P$ 上那个点的即可。
现在的操作 $(x,y,w)$ 就是形如维护祖先序列中的 $w\sum_{x\leq i\leq y}f_i$,可以使用差分的思想,差分成 $x-1$ 处以及 $y$ 处对于树上前缀和的修改,系数分别为 $-w,w$。这个操作赋上颜色 $u$ 表示这是休息点为 $u$ 的贡献,每次 $f$ 只需要询问所有子树中颜色的 $f$ 之和。树状数组维护,时间复杂度 $\mathcal O(n\log n)$。
[自认为实现较为优美的代码](https://loj.ac/s/2203509)。
代码:
#include<bits/stdc++.h>
#define ull unsigned long long
#define ll long long
#define pb push_back
#define mkp make_pair
#define fi first
#define se second
#define inf 1000000000
#define infll 1000000000000000000ll
#define pii pair<int,int>
#define rep(i,a,b,c) for(int i=(a);i<=(b);i+=(c))
#define per(i,a,b,c) for(int i=(a);i>=(b);i-=(c))
#define F(i,a,b) for(int i=a,i##end=b;i<=i##end;i++)
#define dF(i,a,b) for(int i=a,i##end=b;i>=i##end;i--)
#define cmh(sjy) while(sjy--)
#define lowbit(x) (x&(-x))
#define HH printf("\n")
#define eb emplace_back
#define poly vector<int>
#define SZ(x) ((int)x.size())
using namespace std;
template<typename T>inline void chkmax(T &x,const T &y){ x=std::max(x,y); }
template<typename T>inline void chkmin(T &x,const T &y){ x=std::min(x,y); }
const int mod=998244353,maxn=100005;
void fre(){
freopen("mountain.in","r",stdin),freopen("mountain.out","w",stdout);
}
inline int qpow(int x,ll y){
int rt=1;
for(;y;y>>=1,x=1ll*x*x%mod) if(y&1) rt=1ll*rt*x%mod;
return rt;
}
inline void inc(int &x,const int y){ x=(x+y>=mod)?(x+y-mod):(x+y); }
inline void dec(int &x,const int y){ x=(x>=y)?(x-y):(x+mod-y); }
inline void mul(int &x,const int y){ x=1ll*x*y%mod; }
inline int add(const int x,const int y){ return (x+y>=mod)?(x+y-mod):(x+y); }
inline int sub(const int x,const int y){ return (x>=y)?(x-y):(x+mod-y); }
inline int prod(const int x,const int y){ return 1ll*x*y%mod; }
int n,dfn[maxn],siz[maxn],tim,stk[maxn],top,dep[maxn],f[maxn],fa[maxn];
int anc[maxn][20],mn[maxn][20];
int ul[maxn],ur[maxn],uh[maxn],lim[maxn],pre[maxn],fr[maxn],tol[maxn],tor[maxn],diff[maxn],th[maxn];
vector<int>g[maxn],tmp,nxt[maxn];
vector<pii>qu[maxn];
void dfs1(int u){
dfn[u]=++tim,siz[u]=1;
stk[top++]=u;
tmp.push_back(u);
auto find=[&](int k){ return k>dep[u]?0:stk[dep[u]-k]; };
int v=u;
dF(i,18,0)if(anc[v][i]&&mn[v][i]>=lim[u])v=anc[v][i];
fr[u]=fa[v],nxt[fr[u]].push_back(u);
const int L=dep[u]-ul[u]+1,R=dep[u]-ur[u];
th[u]=find(uh[u]+1);
if(lim[u]>=R){
int p=u,to=find(ur[u]+1);
dF(i,18,0)if(anc[p][i]&&mn[p][i]>=R)p=anc[p][i];
qu[to].push_back(mkp(u,mod-1)),qu[to].push_back(mkp(fa[p],1));
inc(diff[fa[p]],mod-1);
}else inc(diff[u],mod-1);
if(lim[u]>=L){
int p=u,to=find(ul[u]);
dF(i,18,0)if(anc[p][i]&&mn[p][i]>=L)p=anc[p][i];
qu[to].push_back(mkp(u,1)),qu[to].push_back(mkp(fa[p],mod-1));
inc(diff[fa[p]],1);
}else inc(diff[u],1);
for(int v:g[u])dfs1(v),siz[u]+=siz[v];
--top;
}
void dfs3(int u){
for(int v:nxt[u])dfs3(v),inc(diff[u],diff[v]);
if(!u)return;
qu[th[u]].push_back(mkp(u,diff[u]));
qu[th[u]].push_back(mkp(fr[u],sub(0,diff[u])));
}
namespace DS{
int t[maxn];
void init(){ memset(t,0,sizeof t); }
void add(int x,int y){ if(x)for(;x<=n;x+=lowbit(x))inc(t[x],y); }
int query(int x){ int R=0;for(;x;x^=lowbit(x))inc(R,t[x]);return R; }
int query(int l,int r){ return l>r?0:sub(query(r),query(l-1)); }
}
void dfs2(int u){
f[u]=(u==1)?1:DS::query(dfn[u],dfn[u]+siz[u]-1);
pre[u]=add(pre[fa[u]],f[u]);
for(auto [x,y]:qu[u])DS::add(dfn[x],1ll*y*pre[u]%mod);
for(int v:g[u])dfs2(v);
}
void solve(){
cin>>n,tim=top=0,dep[0]=-1;
F(i,0,n)g[i].clear(),fr[i]=diff[i]=0,qu[i].clear(),nxt[i].clear();
F(i,2,n)cin>>fa[i]>>ul[i]>>ur[i]>>uh[i],dep[i]=dep[fa[i]]+1,lim[i]=dep[i]-uh[i]-1;
F(i,2,n)g[fa[i]].push_back(i);
F(i,1,n)anc[i][0]=fa[i],mn[i][0]=lim[fa[i]];
F(j,1,18)F(i,1,n)anc[i][j]=anc[anc[i][j-1]][j-1],mn[i][j]=min(mn[i][j-1],mn[anc[i][j-1]][j-1]);
dfs1(1),dfs3(0);
DS::init();
dfs2(1);
F(i,2,n)cout<<f[i]<<' ';
cout<<endl;
}
int testid;
signed main(){
fre(),ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int zsy=1; cin>>testid>>zsy;
F(____,1,zsy)solve();
}
请结合上述文字为这份代码添加注释,越详细越好






 博客内容涉及一个序列操作的问题,其中需要找出使序列所有数变得相同的最少操作次数。通过差分数组和正负数抵消的策略,计算出初始差分数组的正数和负数之和的最大值作为操作数,而它们的绝对差值加1为结果数。代码实现中,首先计算差分数组,然后找出正负数的和,最后输出操作数和结果数。
博客内容涉及一个序列操作的问题,其中需要找出使序列所有数变得相同的最少操作次数。通过差分数组和正负数抵消的策略,计算出初始差分数组的正数和负数之和的最大值作为操作数,而它们的绝对差值加1为结果数。代码实现中,首先计算差分数组,然后找出正负数的和,最后输出操作数和结果数。
















 453
453

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








