树的直径应用

树的毛毛虫形态最大点数问题

原创已于 2022-03-15 22:11:26 修改 · 124 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++

于 2022-03-13 20:53:18 首次发布

这篇博客讨论了一种将树的部分结构抽象为‘毛毛虫’形状的问题。给定一棵树的节点数N和边数M，通过DFS算法找出能够形成最大‘毛毛虫’的节点数，并给出相应的实现代码。文章涉及图论和深度优先搜索算法的应用。

题目描述

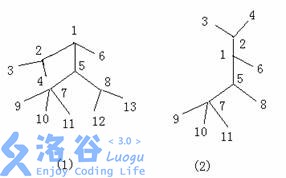
对于一棵树，我们可以将某条链和与该链相连的边抽出来，看上去就象成一个毛毛虫，点数越多，毛毛虫就越大。例如下图左边的树（图 11）抽出一部分就变成了右边的一个毛毛虫了（图 22）。

输入格式

输入中第一行两个整数 N, MN,M，分别表示树中结点个数和树的边数。

接下来 MM 行，每行两个整数 a, ba,b 表示点 aa 和点 bb 有边连接（a, b \le Na,b≤N）。你可以假定没有一对相同的 (a, b)(a,b) 会出现一次以上。

#include<iostream>
#include<cstring>
using namespace std;
const int maxn=3e5+5;
int head[maxn];
struct node{
    int to,next;
}edge[maxn<<1];
int cnt=0;
void add_edge(int from,int to)
{
    edge[cnt].to=to;
    edge[cnt].next=head[from];
    head[from]=cnt++;
}
int s;
int du[maxn];
int as=0;
void dfs(int root,int pre,int all)
{
    if(as<all) s=root,as=all;
    for(int i=head[root];i!=-1;i=edge[i].next)
    {
        int to=edge[i].to;
        if(to!=pre)
        {
            dfs(to,root,all+du[to]-2);
        }
    }
}
int main()
{
    int n,m;cin>>n>>m;
    memset(head,-1,sizeof(head));
    for(int i=1;i<=n;i++) du[i]++;
    for(int i=1;i<=m;i++)
    {
        int from,to;cin>>from>>to;
        add_edge(from,to);
        add_edge(to,from);
        du[from]++;
        du[to]++;
    }
    dfs(1,0,du[1]);
    as=0;
    dfs(s,0,du[s]);
    cout<<as<<endl;
}