hdu1016素数环问题

Problem Description
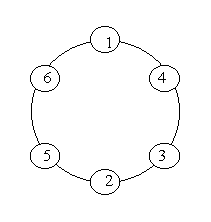
A ring is compose of n circles as shown in diagram. Put natural number 1, 2, …, n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.

Note: the number of first circle should always be 1.

Input
n (0 < n < 20).

Output
The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.

You are to write a program that completes above process.

Print a blank line after each case.

Sample Input

6

8

Sample Output

Case 1:

1 4 3 2 5 6

1 6 5 2 3 4

Case 2:

1 2 3 8 5 6 7 4

1 2 5 8 3 4 7 6

1 4 7 6 5 8 3 2

1 6 7 4 3 8 5 2

一、问题描述：
输入正整数n（n<20），以1为第一个数，把整数1，2，3，…，n组成一个环，使得相邻两个整数的和均为素数。输出时从整数1开始逆时针排列。同一个环应恰好输出一次。

输入、输出如上所述：
（注意输出格式，每个Case之间有一行空白）
（还有每一行最后一个数字后是没有空格的，笔者被坑了两次，哭了，杭电的OJ评测太严格了）

二、问题分析
首先可以生成1~n的全排列，然后逐个判断是否合法，但排列总数高达19！= 121645100408832000 种，时间复杂度是很高的。
其次我们可以采用回溯法，利用dfs算法去求解。在2~n中依次尝试，用数组标记哪些数已经使用过，如果没有被使用且满足和前一个数的和为素数，就标记已经使用，继续dfs，直到满足方案，打印输出。
由于一个数只用一次，所以两个数的和最多为2n-1，所以可以先把前40（甚至前37）个数中的素数找出来，组成一个数组，为以后的判断提供方便。（提示：利用find()函数）。

三、代码（附注释）

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int n, ca = 0; //ca用来打印情况 
int a[20], p[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37}, vis[20]; //a[]数组用来存放答案，p[]存放40以内的素数，vis[]数组用来标记数是否使用过

void dfs(int x)
{
    if (x == n && find(p, p + 12, a[0] + a[n-1]) != p + 12) //递归边界，别忘了第一个数和最后一个数的和也为素数
    {
        for(int i=0;i<n-1;i++)
           cout<<a[i]<<" ";   
        cout<<a[n-1]<<endl;   //被坑的地方，注意格式
    }
    else
        for (int i = 2; i <= n; i++)     //逐个尝试2~n的每个数
            if (!vis[i] && find(p, p + 12, i+a[x-1]) != p + 12)  //如果没有被使用过且和a[]中前一个之和为素数
            {
                a[x] = i;    //满足条件，把i加入a[]数组
                vis[i] = 1;  //标记已经使用过
                dfs(x + 1);
                vis[i] = 0;  //取消标记
            }
}

int main()
{
    while (cin>>n && n)
    {
        memset(a, 0, sizeof(a)); //a[]数组清零
        a[0] = 1;                //第一个数为1
        memset(vis, 0, sizeof(vis)); //vis[]数组清零

        cout<<"Case "<<++ca<<":"<<endl;  
        dfs(1);   //一定要从1开始dfs(),想想为什么
        cout<<endl;
    }
    return 0;
}