电机控制 | 永磁同步电机无位置传感器控制之——滑膜观测器SMO

本文对无位置控制中的滑膜观测器进行思路梳理，并对扩展反电动势进行简要介绍。

知识储备：状态空间方程，符号函数，分情况讨论的概念。

---

一、状态空间方程列写

1.1 反电动势

旋转坐标系下电压方程：

直接变换到静止坐标系下电压方程：

 其中：

 （具体计算过程参考：推个公式 | 三相永磁同步电机静止坐标系下电压方程推导_电机旋转坐标系到静止坐标系推导-优快云博客）

可以看出，方程内有两处包含位置角信息，且存在sin2θ项，不便于θ信息获取。扩展反电动势应运而生。

---

1.2 扩展反电动势

对原电压方程改写：

 变换到静止坐标系下电压方程：

上式即为同步电机的数学模型通式。

当Ld≠Lq时，为内嵌式同步电机公式；

当Ld=Lq时，为表贴式同步电机公式；

当KE=0时，为同步磁阻电机公式。

我们定义后一项为扩展反电动势，静止坐标系下的电压方程写作：

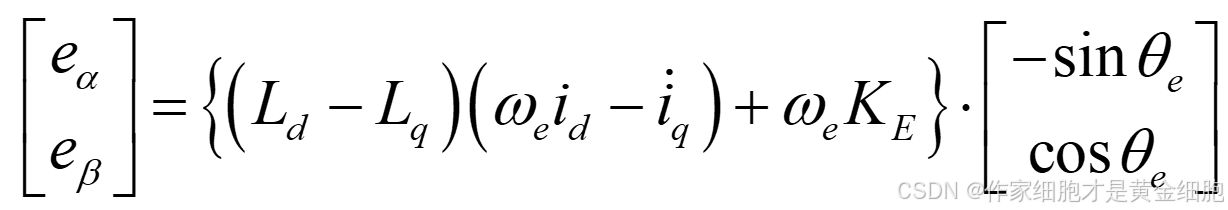
可以看到，此时只有扩展反电动势中包含转子位置角。因此我们需要获取扩展反电动势信息，进而得到角度，从而实现无位置控制。

我们是在电流环中进行控制，即被控量是电流。因此，我们把被控量放在等式左边，重写状态空间方程为：

（本文主要为了理解思路，因此以简单情况切入）假设Ld=Lq，电机参数已知，则通过上式子我们可以直接算出扩展反电动势值，后文简称“反电动势”。但是在实际情况下，由于各种干扰等存在，计算出的值并不准确，存在较大误差，因此我们采用滑膜观测器来进行反电动势获取。

---

二、滑膜观测器

2.1 反电动势估计

首先对估计电流和反电动势进行列写：

直接控不好控，我们做差间解控。用估计值-实际值：

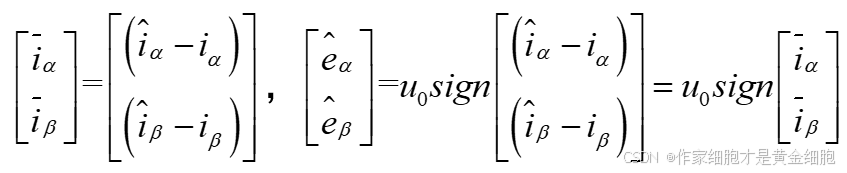
当估计值和实际值等价时，我们估计的反电动势就等于实际的反电动势了（这里采用常值切换函数sign）。这就是滑动模态，要保证这个滑动模态一直存在，要保证V*V‘ < 0（李雅普诺夫第二法则），即：

观察上式可知，A项一定小于零，B项分情况可以写为：

至此，确定了滑膜控制面的值，即得到了估计的反电动势值。

---

2.2 反正切获取转子位置及转速

反电动势中包含转子位置信息即：

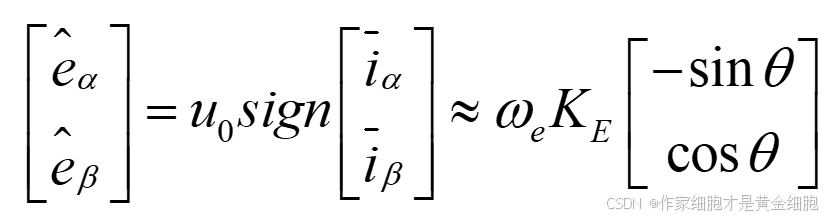
转速及转子位置角获取：

---

补充：

李雅普诺夫第二法则：对于连续时间系统，如果存在一个连续可微的李雅普诺夫函数，满足以下两个条件：

1.正定，即 ；

2.负定，即；

则系统渐近稳定，综上总结为： 

---

仿真结果分析：电机控制 | 基于反正切的滑膜观测电机控制仿真及问题记录-优快云博客 

---

参考博客：【电机控制】PMSM无感FOC控制（七）滑模观测器的应用_滑膜观测器-优快云博客

如果此篇文章对您有帮助，记得评论告诉我(●'◡'●)，您的点赞和收藏是对写作者最大的鼓励！