牛客的小白月赛24补题

我就是不信J题能错！

。。。。。。。没注意负数取模
呀呀呀呀，打脑壳

保证取模后的结果为正数：
((x % MOD) + MOD) % MOD

思路
1.挨个尝试肯定超时
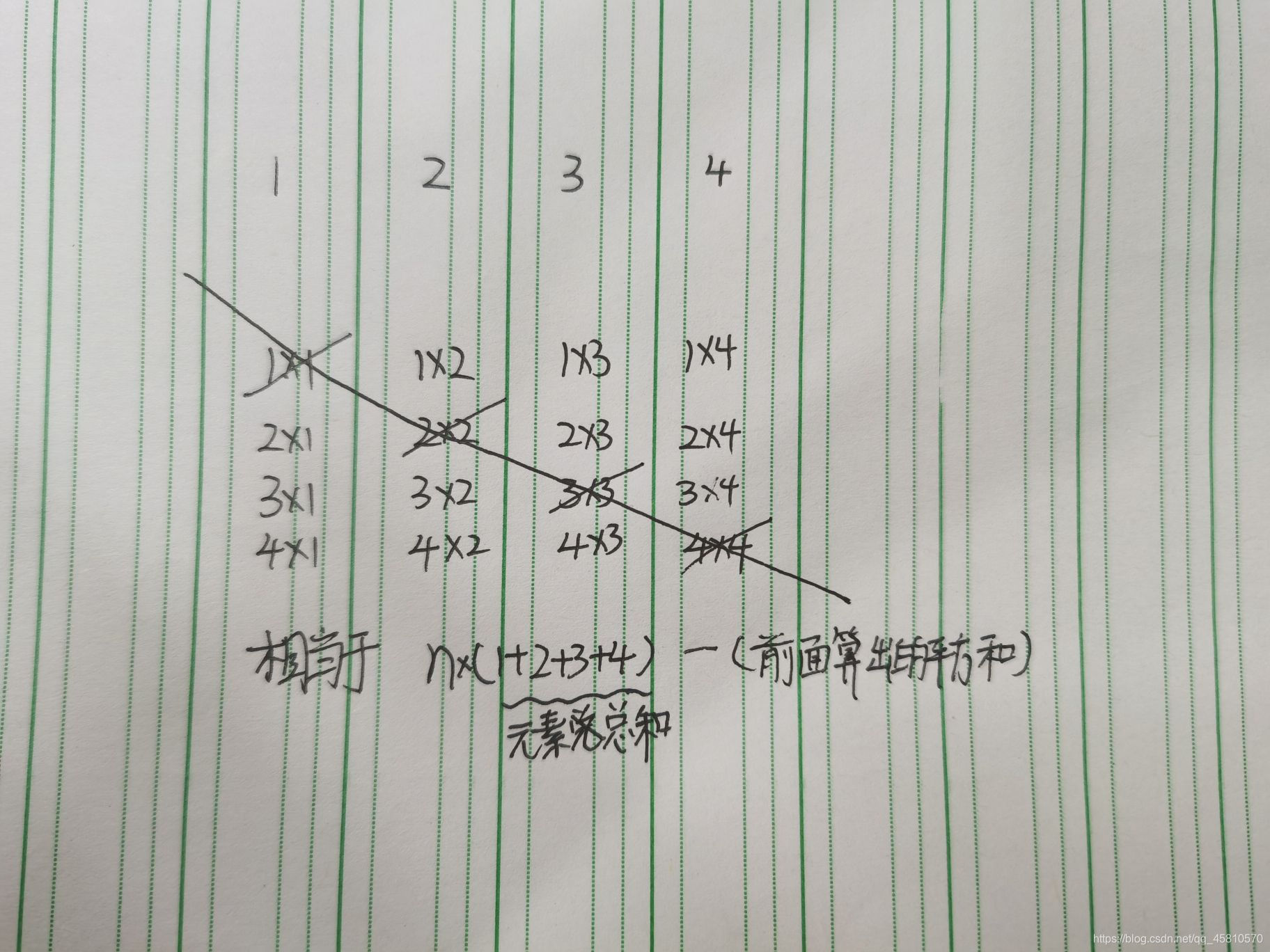
2.就是把平方项展开

a²+b²+2ab
每个平方项的出现次数n-1次
每个2ab形式的和

最后一定注意取余为正数

戳我试试看

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<list> 
using namespace std;
#define mid 1000000007 
typedef  long long ll;
ll c[500005];
int main(){
    ll a,i;
    ll sum=0,sum2=0,sum3=0;
    scanf("%lld",&a);
    for(i=0;i<a;i++){
    scanf("%lld",&c[i]);
    sum=(sum+c[i])%mid;
    sum2=(sum2+(c[i]*c[i])%mid)%mid;
    }
    for(i=0;i<a;i++){
        sum3=(c[i]*sum%mid+sum3)%mid;
    }
    cout<<((sum2*(a-1)%mid-(sum3-sum2)%mid)+mid)%mid;
    return 0;
}

C题十面埋伏

比赛的时候看都没看~~~~~~

牛客大神估的是

1800

但做起来还是相当轻松，就是一个相当清晰的搜索
就是有点小技巧
我在题中记录

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<list>  
using namespace std;
#define mid 1000000007  
typedef  long long ll;
//第一个思路（多半错，但我想不出哪里错）
//就是检测每个' . '，看它上下左右是不是有'#'，有的话，就变为*;
//果然错了，因为如果#围成一个空心圈，就会把中间的也变了
//第二个思路————搜索 
int w[4][2]={{0,1},{0,-1},{-1,0},{1,0}};
int a,b;
char c[506][506];
int book[506][506]; 
void sou(int x,int y){
	int i;
	for(i=0;i<=3;i++){//平常一样，一个点向4个方向走 
		int fx=x+w[i][0];
		int fy=y+w[i][1];
		if(fx>=1&&fx<=a&&fy>=1&&fy<=b){//害怕越界 
			if(c[fx][fy]=='.'&&book[fx][fy]==0){/*如果走后的落脚点是个没有走过的'.', 
												就以这个点再进行搜索，并且标记走过*/ 
					book[fx][fy]=1;
					sou(fx,fy);
				}
			if(c[fx][fy]=='#'){//我们认定#号点是走不通的，遇见就把原本的点标记为* 
				c[x][y]='*';
			}
		}
	}
}
int main(){
	int i,j;
	cin>>a>>b;
	for(i=1;i<=a;i++){
		for(j=1;j<=b;j++){
			cin>>c[i][j];
		}
	}
	book[1][1]=1;
	sou(1,1);
	for(i=1;i<=a;i++){
		for(j=1;j<=b;j++){
			cout<<c[i][j];
		}
		cout<<endl;
	}
} 

我的补题原则是
只补错的，
简单的，
能够理解领悟的，
看着不会做但是代码短的