本文详细介绍了二叉树的各种遍历方法，包括递归和非递归实现的先序、中序、后序遍历以及宽度优先遍历。此外，还探讨了如何判断一棵二叉树是否是搜索二叉树、完全二叉树、满二叉树或平衡二叉树。同时，提供了寻找两个节点的最低公共祖先和一个节点的后继节点的算法。最后，讨论了二叉树的序列化和反序列化以及折纸问题的模拟。
文章目录
1.二叉树的遍历
二叉树节点结构：
(1)用递归和非递归两种方式实现二叉树的先序（dfs）、中序、后序遍历
递归序：对于每个节点，递归时都可以回到自己三次。在递归序的基础之上可以加工出三种遍历顺序：先序（头左右）、中序（左头右）、后序（左右头），分别是第一次到自己打印，后两次到自己什么也不干；第二次到自己打印，其余两次到自己什么也不干；第三次到自己打印，其余两次到自己什么也不干。利用递归序可以三次访问自己，选择打印时机不同，产生出三种递归的遍历方式。
//递归序
void f(Node* head) {
//1
if (head == nullptr) {
return;
}
//1
f(head->left);
//2
//2
f(head->right);
//3
//3
}
非递归：
先序：准备一个栈；首先将头节点放入栈中；每次在栈中弹出一个节点记为cur；打印（处理）cur；先将右孩子入栈，再将左孩子入栈（如果有）；重复上述操作栈为空
后序：先序：“头左右”；先序撇：“头右左”，该打印时不打印，而是将其放入一个辅助栈里，所有节点入栈之后统一打印—>后序遍历。因为有辅助栈的缘故，“头右左”变成了“左右头”，即后序。
中序：准备一个栈；每棵子树整棵树左边界进栈，依次弹出节点的过程中打印，然后对弹出节点的右树重复上述过程，直到栈为空。
先序遍历代码实现：
//先序遍历
//递归
void preOrderRecursion(Node* head) {
if (head == nullptr) {
return;
}
cout << head->val << " ";
preOrderRecursion(head->left);
preOrderRecursion(head->right);
}
//非递归
void preOrderUnRecur(Node* head) {
if (head != nullptr) {
stack<Node*>sk;
sk.push(head);
while (!sk.empty()) {
head = sk.top();
sk.pop();
cout << head->val << " ";
if (head->right != nullptr) {
sk.push(head->right);
}
if (head->left != nullptr) {
sk.push(head->left);
}
}
}
}
中序遍历代码实现：
//中序遍历
//递归
void inOrderRecursion(Node* head) {
if (head == nullptr) {
return;
}
inOrderRecursion(head->left);
cout << head->val << " ";
inOrderRecursion(head->right);
}
//非递归
void inOrderUnRecur(Node* head) {
if (head != nullptr) {
stack<Node*>sk;
while (!sk.empty() || head != nullptr) {
if (head != nullptr) {//左边界进栈
sk.push(head);
head = head->left;
}
else {//弹出就打印
head = sk.top();
sk.pop();
cout << head->val << " ";
head = head->right;
}
}
}
}
后序遍历代码实现：
//后序遍历
//递归
void postOrderRecursion(Node* head) {
if (head == nullptr) {
return;
}
postOrderRecursion(head->left);
postOrderRecursion(head->right);
cout << head->val << " ";
}
//非递归
void postOrderUnRecur(Node* head) {
if (head != nullptr) {
stack<Node*>s1;
stack<Node*>s2;
s1.push(head);
while (!s1.empty()) {
head = s1.top();
s1.pop();
s2.push(head);
if (head->left != nullptr) {
s1.push(head->left);
}
if (head->right != nullptr) {
s1.push(head->right);
}
}
while (!s2.empty()) {
head = s2.top();
cout << head->val << " ";
s2.pop();
}
}
}
(2)如何完成二叉树的宽度优先遍历（bfs）(常见题目：求一棵二叉树的宽度)
二叉树的宽度优先遍历（一层一层的遍历），用队列；首先将头节点放入队列中；弹出就打印；然后先放左再放右
代码实现：
//宽度优先遍历
void bfs(Node* head) {
if (head != nullptr) {
queue<Node*>q;
q.push(head);
while (!q.empty()) {
head = q.front();
q.pop();
cout << head->val << " ";
if (head->left != nullptr) {
q.push(head->left);
}
if (head->right != nullptr) {
q.push(head->right);
}
}
}
}
例：求一棵二叉树的宽度
解：
方法一：需要知道当前在第几层，并且知道这一层有多少节点。用一个hashmap记录当前节点在第几层（key：node，value：所在层）
看代码的时候，将变量写出来，画图看
方法二：不用hashmap。需要用到几个变量：curend：当前层最后一个节点、nextend：下一层最后一个节点（始终是最近进栈的节点，换层的时候要置空）、curlevel当前层已经发现的节点数
代码实现：
//例：求一棵二叉树的宽度
//方法一：使用hashmap
int maxW01(Node* head) {
if (head == nullptr) {
return 0;
}
queue<Node*>q;
q.push(head);
unordered_map<Node*, int>mp;
mp.insert({ head,1 });
int curLevel = 1;//当前遍历所在的层
int curLevelNodes = 0;//当前层节点数,节点出栈再增加
int maxNodes = INT_MIN;
while (!q.empty()) {
head = q.front();
q.pop();
int curNodeLevel = mp[head];//当前节点所在的层
if (curNodeLevel == curLevel) {
curLevelNodes++;
}
else {
maxNodes = max(maxNodes, curLevelNodes);;
curLevel++;
curLevelNodes = 1;
}
if (head->left != nullptr) {
q.push(head->left);
mp.insert({ head->left,curLevel + 1 });
}
if (head->right != nullptr) {
q.push(head->right);
mp.insert({ head->right,curLevel + 1 });
}
}
return max(maxNodes, curLevelNodes);//最后一层的curLevelNodes没有于maxNodes比较
}
//方法二：不适用hashmap
int maxW02(Node* head) {
if (head == nullptr) {
return 0;
}
queue<Node*>q;
q.push(head);
Node* curEndNode = head;//当前层最后一个节点
Node* nextEndNode = nullptr;//下一层最后一个节点
int curLevelNodes = 0;//当前层已经发现的节点数
int maxNodes = INT_MIN;
while (!q.empty()) {
head = q.front();
q.pop();
curLevelNodes++;
//要先将左右子树进栈，以更新nextEndNode
if (head->left != nullptr) {
q.push(head->left);
nextEndNode = head->left;
}
if (head->right != nullptr) {
q.push(head->right);
nextEndNode = head->right;
}
//相等，需要换层
if (head == curEndNode) {
maxNodes = max(maxNodes, curLevelNodes);
curEndNode = nextEndNode;
nextEndNode = nullptr;
curLevelNodes = 0;
}
}
return maxNodes;
}
2.二叉树的相关概念及其实现判断
(1)如何判断一颗二叉树是否是搜索二叉树？
搜索二叉树：左子树的节点都比根节点小，有子树的节点都比根节点大（经典搜索二叉树没有重复值）
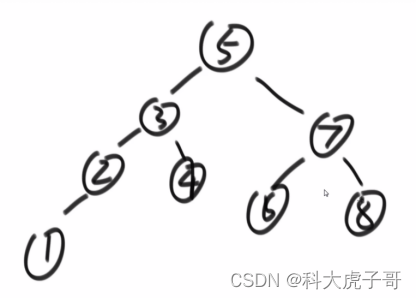
判断方法：中序遍历一直是升序的则为搜索二叉树，否则不是。
代码实现：
//判断一颗二叉树是否是搜索二叉树
//递归
bool checkSbtRecur(Node* head) {
if (head == nullptr) {
return true;
}
bool checkLeft = checkSbtRecur(head->left);
//打印时机，变成了比较实际
if ((checkLeft == false) || (head->left!=nullptr&& head->val <= head->left->val)) {
return false;
}
bool checkRight = checkSbtRecur(head->right);
return checkRight;
}
//非递归
bool checkSbtUnRecur(Node* head) {
if (head == nullptr) {
return true;
}
stack<Node*>sk;
int preVal = INT_MIN;
while (!sk.empty() || head != nullptr) {
if (head != nullptr) {
sk.push(head);
head = head->left;
}
else {
head = sk.top();
sk.pop();
if (head->val <= preVal) {
return false;
}
preVal = head->val;
head = head->right;
}
}
return true;
}
(2)如何判断一颗二叉树是完全二叉树？
判断方法：按照宽度遍历，依次遍历每个结点的过程中：1)有右孩子没左孩子，返回false；2)在1)不违规的情况下，第一次遇到左右孩子不双全节点，之后的所有节点必须是叶子节点
//判断一颗二叉树是完全二叉树
bool checkCBT(Node* head) {
if (head == nullptr) {
return true;
}
queue<Node*>q;
q.push(head);
bool flag = false;//是否遇到左右两个孩子不双全的节点
while (!q.empty()) {
head = q.front();
q.pop();
if ((head->right != nullptr && head->left == nullptr)||(flag&&(head->left!=nullptr||head->right!=nullptr))) {
return false;
}
if (head->left == nullptr || head->right == nullptr) {//判断是否左右孩子不双全
flag = true;
}
if (head->left != nullptr) {
q.push(head->left);
}
if (head->right != nullptr) {
q.push(head->right);
}
}
return true;
}
(3)如何判断一颗二叉树是否是满二叉树？
麻烦的方法：先求二叉树的深度L，再求二叉树节点数N，判断是否满足
用套路解：向左树要深度和节点数、向右树要深度和节点数，最后再进行判断是否满足
//判断一颗二叉树是否是满二叉树
struct ReDa {
int depth;
int nodes;
bool isFbt;
ReDa(int depth, int nodes, bool isFbt) {
this->depth = depth;
this->nodes = nodes;
this->isFbt = isFbt;
}
};
ReDa isFull(Node* head) {
if (head == nullptr) {
return ReDa(0, 0, true);
}
ReDa leftData = isFull(head->left);
ReDa rightData = isFull(head->right);
int depth = max(leftData.depth, rightData.depth) + 1;
int nodes = leftData.nodes + rightData.nodes + 1;
bool isFbt = (nodes == pow(2, depth) - 1) ? true : false;
return ReDa(depth, nodes, isFbt);
}
(4)如何判断一颗二叉树是否是平衡二叉树？（二叉树递归套路）
平衡二叉树：任意一个节点，左树的高度和右树的高度差不超过1
套路：求解一个二叉树问题时，我可以向我的左树要信息，可以向我的右树要信息的情况下，列出可能性，向上层递归返回我这一层的信息。可以解决一切树型DP（动态规划）的问题，二叉树中最难的问题。
假设以x为头的子树，判断他是不是平衡二叉树，可以向我的左树要信息，可以向我的右树要信息的情况下，罗列可能性；1) 左子树要是平衡二叉树；2) 右子树要是平衡二叉树；3) 左子树、右子树的高度差小于2;这里只有一种可能性：以上三个条件都成立。所以左树需要给我：它是否是平的和高度；右树需要给我：它是否是平的和高度。
//判断一颗二叉树是否是平衡二叉树(套路)
struct ReturnData{
bool isBalance;
int hight;
ReturnData(bool isBalance, int hight) {
this->isBalance = isBalance;
this->hight = hight;
}
};
ReturnData isBalanced(Node* head) {
if (head == nullptr) {//base case搞清楚
return ReturnData(true, 0);
}
ReturnData leftData = isBalanced(head->left);
ReturnData rightData = isBalanced(head->right);
int height = max(leftData.hight, rightData.hight) + 1;
bool isBal = leftData.isBalance && rightData.isBalance && abs(leftData.hight - rightData.hight) < 2;
return ReturnData(isBal, height);
}
(5)利用套路再实现判断搜索二叉树
思路：以x为头的整棵树是否为搜索二叉树，可以问左树要信息，也可以问右树要信息，罗列可能性：1) 左树是搜索二叉树；2) 右树是搜索二叉树；3) 左树最大值要小于x的值；4) 右树的最小值要大于x的值。所以问左树要的信息是：你是否为搜索二叉树以及你的最大值；问右树要的信息是：你是否为搜索二叉树以及你的最小值。问左右子树要的信息不再一样，但是递归要求对每个节点一视同仁，所以取索要信息的并集，即左右子树都返回是否为搜索二叉树、最小值、最大值。
代码实现：
//利用套路判断是否为搜索二叉树
struct ReturnType {
bool isSBT;
int minVal;
int maxVal;
ReturnType(bool isSBT, int minVal, int maxVal) {
this->isSBT = isSBT;
this->minVal = minVal;
this->maxVal = maxVal;
}
};
ReturnType* isSBT(Node* head) {
if (head == nullptr) {
return nullptr;//basecase为空时不知道怎么设置，直接返回空，但在调用的时候要做判断
}
ReturnType* leftData = isSBT(head->left);
ReturnType* rightData = isSBT(head->right);
bool isS = true;
int minV = head->val;
int maxV = head->val;
if (leftData != nullptr) {
minV = min(minV, leftData->minVal);
maxV = max(maxV, leftData->maxVal);
}
if (rightData != nullptr) {
minV = min(minV, rightData->minVal);
maxV = max(maxV, rightData->maxVal);
}
if (leftData != nullptr && (!leftData->isSBT || leftData->maxVal >= head->val)) {
isS = false;
}
if (rightData != nullptr && (!rightData->isSBT || rightData->minVal <= head->val)) {
isS = false;
}
return new ReturnType(isS, minV, maxV);
}
3.给定两个二叉树的节点node1和node2，找到他们的最低公共祖先节点
最低公共祖先：最先汇聚的节点。
解：
方法一：用一个hashmap存储节点与该节点的父节点（遍历）；然后将node1向上遍历至头节点，每遍历到一个节点都将其放入set中；最后node2也向上遍历至头节点，每遍历到一个节点都检查是否再set中，如果在则返回
方法二：1) n1是n2的lca或n2是n1的lca；2) n1和n2不互为lca。问左树有没有n1/n2；问右树有没有n1/n2，有则返回最近的那个（都有的情况），没有则返回空
代码实现：
//给定两个二叉树的节点node1和node2，找到他们的最低公共祖先节点
//方法一：
void process(Node* head, unordered_map<Node*, Node*>& mp) {
if (head == nullptr) {
return;
}
mp.insert({ head->left,head });
mp.insert({ head->right,head });
process(head->left, mp);
process(head->right, mp);
}
Node* lca01(Node* head, Node* n1, Node* n2) {
unordered_map<Node*, Node*>mp;
mp.insert({ head,head });
process(head, mp);
unordered_set<Node*>st;
while (n1 != mp[n1]) {
st.insert(n1);
n1 = mp[n1];
}
while (n2 != mp[n2]) {
if (st.find(n2) != st.end()) {
return n2;
}
n2 = mp[n2];
}
return head;
}
//方法二：
Node* lca02(Node* head, Node* n1, Node* n2) {
if (head == nullptr || head == n1 || head == n2) {
return head;
}
Node* left = lca02(head->left, n1, n2);
Node* right = lca02(head->right, n1, n2);
//左右都不为空返回当前节点即为lca（case2）
if (left != nullptr && right != nullptr) {
return head;
}
//一个为空，一个不为空返回不为空的那个（case1）
return left == nullptr ? right : left;
}
4.在二叉树中找到一个节点的后继节点
后继节点：在二叉树的中序遍历的序列中，node的下一个节点叫作node的后继节点；前驱节点：在二叉树的中序遍历的序列中，node的前一个节点叫作node的前驱节点
一般的方法是采用中序遍历，找到一个节点的后继节点（O(N)），但是该题给出了一个parent指针，可以优化(O(k),k为节点与其后继节点的真实距离)。在结构上找到一个节点的后继节点的规律：1) x有右树时，则x的后继为x右树上最左节点；2) x无右树时，则x的后继一定在x的上面，根据parent指针向上找，直到当前节点时其父节点的左孩子，则x的后继即为这个父节点（考虑特殊情况：x为整棵树的最右节点，向上找直到为空也没找到，那么x的后继就是空）。
代码实现：
//在二叉树中找到一个节点的后继节点
struct Node_ {
int val;
Node_* left;
Node_* right;
Node_* parent;
Node_(int val) {
this->val = val;
this->left = nullptr;
this->right = nullptr;
this->parent = nullptr;
}
};
Node_* getSuccessorNode(Node_* n) {
if (n == nullptr) {
return nullptr;
}
if (n->right != nullptr) {//有右树
Node_* p = n->right;
while (p->left != nullptr) {
p = p->left;
}
return p;
}
else {//无右树
Node_* p = n->parent;
while (p != nullptr && n != p->left) {
n = p;
p = p->parent;
}
return p;
}
return nullptr;
}
5.二叉树的序列化和反序列化
序列化：树–>字符串
反序列化：字符串–>树
先序 中序 后序都可以序列化
先序为例：
序列化就是将遍历时的打印操作换成字符串操作。
代码实现：
//序列化
string serialByPre(Node* head) {
if (head == nullptr) {
return "#_";//用#表示空，_是一个节点的结束
}
string res = to_string(head->val) + "_";//to_string将各种数转成string 需要头文件string
res += serialByPre(head->left);
res += serialByPre(head->right);
return res;
}
//反序列化
queue<string> splitStr(string str, char spS) {
string s = "";
queue<string>res;
for (auto c : str) {
if (c == spS) {
res.push(s);
s = "";
}
else {
s = s + c;
}
}
return res;
}
Node* reconPreOrder(queue<string>& q) {
string s = q.front();
q.pop();
if (s == "#") {
return nullptr;
}
int val = stoi(s);
Node* head = new Node(val);
head->left = reconPreOrder(q);
head->right= reconPreOrder(q);
return head;
}
Node* reconByPreString(string s) {
queue<string>q = splitStr(s, '_');
return reconPreOrder(q);
}
6.折纸问题
模拟中序遍历：
代码实现：
//折纸问题
void printProcess(int i, int N, bool down) {//i:节点所在层 N：一共多少层 down：打印凹（true）还是凸（false）
if (i > N) {
return;
}
printProcess(i + 1, N, true);
if (down == true) {
cout << "凹";
}
else {
cout << "凸";
}
printProcess(i + 1, N, false);
}
void printAllFolds(int N) {
printProcess(1, N, true);
cout << endl;
}
扫一扫
1248
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
