🥳🥳PS:此篇开头的链表习题补充在了P4的末尾!!🥳🥳
目录
一、二叉树的节点结构:
// 定义二叉树节点结构
typedef struct TreeNode {
int value; // 节点值
struct TreeNode* left; // 指向左子节点的指针
struct TreeNode* right; // 指向右子节点的指针
} TreeNode;Q:
1、用递归和非递归的方式实现二叉树的先序、中序、后续遍历
2、如何直观地打印一颗二叉树
3、如何完成二叉树的宽度优先搜索(常见题目:求一颗二叉树的宽度)
二、树的递归序以及递归遍历
如下图所示,在递归遍历中,二叉树会有如下的1、2、3次机会回到自身的函数中。我们可以在其中穿插打印/求和等一系列操作以实现对于树结构的使用。

按照“递归序”来理解前序、中序、后序遍历:

三、二叉树的非递归遍历
本质上说,递归函数自动实行了压栈、弹栈功能,如果自己实现,即可达到同样的效果,这样更有利于我们理解递归的过程:
1. 先序遍历的非递归实现:

2. 后序遍历的非递归实现:

3. 中序遍历的非递归实现:

网上的非递归实现二叉树的动画讲解很多,大家可以看看这两个:
二分搜索树 前中后序(递归和非递归)和层序遍历(动图)
二叉树遍历-先序(非递归)【图解+代码】_哔哩哔哩_bilibili
下面我们再来看一个例子,动手理解下面树的非递归中序遍历:
例:
按照上述方法,对下面的树,画图实现非递归中序遍历:
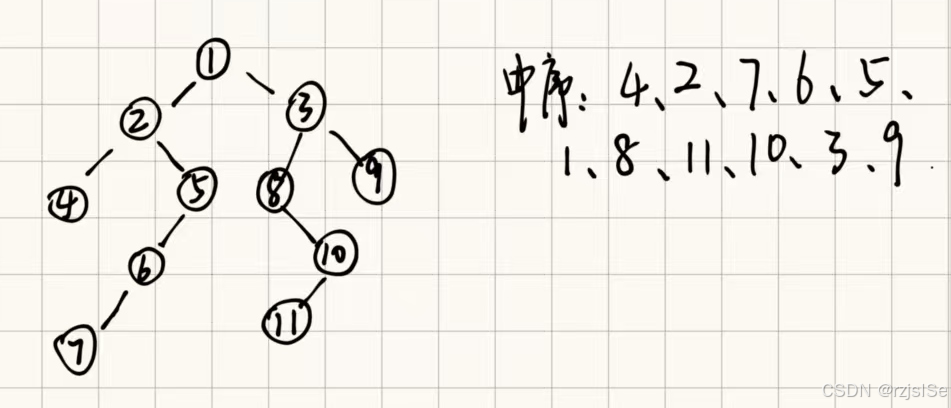
大家可以参考我绘制的过程:

四、层序遍历(宽度遍历)
步骤:
1)维护一个队列;
2)对于一颗树,先将头节点放入;
3)弹出队列中节点,并将其左节点、右节点依次放入(若有);
4)重复2~3,直到队列为空;
代码实现(c++):
// 层序遍历函数
void levelOrderTraversal(TreeNode* root) {
if (root == nullptr) return; // 如果树为空,直接返回
std::queue<TreeNode*> q; // 创建一个队列
q.push(root); // 将根节点入队
while (!q.empty()) {
TreeNode* current = q.front(); // 访问队头节点
q.pop(); // 出队
std::cout << current->value << " "; // 输出节点值
// 将当前节点的左子节点和右子节点入队
if (current->left != nullptr) {
q.push(current->left);
}
if (current->right != nullptr) {
q.push(current->right);
}
}
}变体例题:求一颗二叉树的宽度?
tips:这里并未按照原视频设置那么多变量,而是采用“BFS+队列长度“来对于二叉树进行判断!
- 时间复杂度:O(n),其中 n 是二叉树的节点数。我们遍历每个节点一次。
- 空间复杂度:O(n),队列中最多会存储二叉树的一层节点,即最宽的一层的节点数。在最坏的情况下,队列的最大容量为树的宽度。
struct TreeNode {
int value;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : value(val), left(nullptr), right(nullptr) {}
};// 计算二叉树的宽度
int calculateTreeWidth(TreeNode* root) {
if (root == nullptr) return 0; // 如果树为空,宽度为 0
std::queue<TreeNode*> q; // 使用队列进行层序遍历
q.push(root); // 将根节点入队
int maxWidth = 0; // 记录最大宽度
// 层序遍历
while (!q.empty()) {
int levelSize = q.size(); // 当前层的节点数
maxWidth = std::max(maxWidth, levelSize); // 更新最大宽度
// 遍历当前层的所有节点
for (int i = 0; i < levelSize; ++i) {
TreeNode* current = q.front();
q.pop();
// 将左子节点和右子节点入队
if (current->left != nullptr) {
q.push(current->left);
}
if (current->right != nullptr) {
q.push(current->right);
}
}
}
return maxWidth; // 返回最大宽度
}int main() {
// 创建一个简单的二叉树
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
root->right->right = new TreeNode(6);
// 计算并输出二叉树的最大宽度
std::cout << "Maximum width of the tree: " << calculateTreeWidth(root) << std::endl;
return 0;
}重要!看代码注意用纸笔画图理解!硬看需要很多经验,新手最好一步一个脚印!
五、经典问题
1、如何判断搜索二叉树?
搜索二叉树:左子树的值总有 < 根 < 右子树;
判断:联想到中序遍历,输出中序遍历结果,若是升序,则是搜索二叉树!
// 中序遍历判断是否是搜索二叉树
bool inOrderTraversal(TreeNode* root, int& prev) {
if (root == nullptr) return true;
// 先遍历左子树
if (!inOrderTraversal(root->left, prev)) {
return false;
}
// 检查当前节点值是否大于前一个节点值
if (root->value <= prev) {
return false;
}
// 更新前一个节点的值为当前节点值
prev = root->value;
// 再遍历右子树
return inOrderTraversal(root->right, prev);
}
// 检查树是否为搜索二叉树
bool isBinarySearchTree(TreeNode* root) {
int prev = INT_MIN; // 用于记录前一个节点的值
return inOrderTraversal(root, prev);
}2、如何判断完全二叉树?
完全二叉树:除最后一层,其余层都是满的;且最后一层从左到右依次填充。
判断:基于BFS——(1)对任意节点,若其有右节点但无左节点,return false;
(2)在(1)的前提下,从遇到第一个左右节点不全的节点开始,后续只能是
叶子节点;

// 检查是否为完全二叉树
bool isCompleteBinaryTree(TreeNode* root) {
if (root == nullptr) return true;
std::queue<TreeNode*> q;
q.push(root);
bool leaf = false; // 标记出现叶子节点
while (!q.empty()) {
TreeNode* current = q.pop();
l = current->left;
r = current->right;
if(
// 左右节点不全且有孩子(违反条件2)
(leaf && (l || r))
||
(!l && r) // 无左节点,却有右节点(违反条件1)
){
return false;
}
// 如果当前节点是非叶节点,继续入队
if (l) {
q.push(l);
}
if (r) {
q.push(r);
}
if(l || r){
leaf = true;
}
}
return true; // 遍历完整棵树且未违反条件
}
3、如何判断满二叉树?
满二叉树:若树的最大深度为L,节点数为N,则当且仅当满足 N = 2^L -1 时,为满二叉树。
思路:求树高和节点数,验证等式是否成立。
// 计算树的高度
int calculateHeight(TreeNode* root) {
int height = 0;
while (root) {
height++;
root = root->left; // 一直走左子树,直到最深的叶子节点
}
return height;
}
// 计算树的节点数
int countNodes(TreeNode* root) {
if (!root) return 0;
queue<TreeNode*> q;
q.push(root);
int nodeCount = 0;
while (!q.empty()) {
TreeNode* current = q.front();
q.pop();
nodeCount++;
if (current->left) q.push(current->left);
if (current->right) q.push(current->right);
}
return nodeCount;
}
// 判断是否为满二叉树
bool isFullBinaryTree(TreeNode* root) {
if (!root) return true; // 空树也是满二叉树
int height = calculateHeight(root);
// 计算理论上的节点数 N = 2^L - 1
int expectedNodes = (1 << height) - 1;
int actualNodes = countNodes(root);
// 判断节点数是否相等
return expectedNodes == actualNodes;
}六*、二叉树递归套路(树形DP)
当可以向左树和右树要信息的时候,需要什么信息,可以达成目的?
平衡二叉树:对于任意子树,其左树和右树的高度差不超过1。
此处以平衡二叉树为例,需同时满足以下三个条件:
(1)左树为平衡二叉树;
(2)右树为平衡二叉树;
(3)|h左 - h右| <= 1;
整理可得:左树需得到信息——是否平衡、高度是多少;右树也需得到信息——是否平衡、高度是多少。故可确定返回值的结构体为:是否是平衡二叉树 + 树高。
代码实现:
#include <bits/stdc++.h>
#include <iostream>
#include <cmath>
using namespace std;
struct Node{
int val;
Node* left;
Node* right;
// 记得写构造函数!
Node(int value) : val(value), left(nullptr), right(nullptr) {}
};
struct ReturnType{
bool isB;
int ht;
};
ReturnType isBST(Node* root, int h){
if(root == NULL){
return ReturnType{true, 0};
}
ReturnType l = isBST(root->left, h);
ReturnType r = isBST(root->right, h);
bool isBalanced = l.isB && r.isB && (abs(l.ht - r.ht) <= 1);
int ht=max(l.ht, r.ht)+1;
return ReturnType{isBalanced, ht};
}
int main()
{
// 创建一棵平衡二叉树
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->left = new Node(6);
// 判断是否为平衡二叉树
if (isBST(root, 0).isB) {
cout << "The tree is balanced." << endl;
} else {
cout << "The tree is NOT balanced." << endl;
}
}
搜索二叉树同理:从向左右子树要信息的角度思考,需满足如下条件:
- 左树是搜索二叉树;
- 右树是搜索二叉树;
- 左max < root;
- 右min > root;
整理可得(取并集),返回的值:是否是搜索二叉树 + min + max。
代码:
#include <bits/stdc++.h>
#include <cmath>
#include <iostream>
using namespace std;
struct Node{
int val;
Node* left;
Node* right;
Node(int v): val(v), left(nullptr), right(nullptr) {}
};
struct ReturnType{
bool isST;
int min;
int max;
};
ReturnType process(Node* root){
if(root == NULL){
return ReturnType{true, INT_MAX, INT_MIN}; // 注意叶节点初始化为无穷以免影响判断
}
ReturnType l = process(root->left);
ReturnType r = process(root->right);
bool isSearchTree = l.isST && r.isST && (l.max < root->val) && (r.min > root->val);
// 全局最大 / 最小值
int min1 = min(root->val, l.min);
min1 = min(min1, r.min);
int max1 = max(root->val, l.max);
max1 = max(max1, r.max);
return ReturnType{isSearchTree, min1, max1};
}
int main()
{
// 创建一棵二叉树
Node* root = new Node(10);
root->left = new Node(8);
root->right = new Node(12);
root->left->left = new Node(4);
root->left->right = new Node(9);
root->right->left = new Node(11);
// 判断是否为搜索二叉树
ReturnType result = process(root);
cout << "Is it a search binary tree? " << (result.isST ? "Yes" : "No") << endl;
return 0;
}同理,使用套路解满二叉树的判断:
需要满足的条件:
左右子树都是满二叉树;
返回值:树的深度,树的节点个数;
代码实现:
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
struct Node{
int val;
Node* left;
Node* right;
Node(int v): val(v), left(nullptr), right(nullptr) {}
};
struct Info{
int height;
int nodeSum;
};
Info process(Node* root){
if(root == NULL){
return Info{0, 0};
}
Info inLeft = process(root->left);
Info inRight = process(root->right);
int h = max(inLeft.height, inRight.height)+1;
int nodeSum = inLeft.nodeSum + inRight.nodeSum + 1;
return Info{h, nodeSum};
}
int main()
{
Node* root = new Node(10);
root->left = new Node(8);
root->right = new Node(12);
root->left->left = new Node(4);
root->left->right = new Node(9);
root->right->left = new Node(11);
root->right->right = new Node(2);
Info result = process(root);
cout<< (result.nodeSum == (1 << result.height)-1 ? "Yes":"no");
return 0;
}“套路”仅仅适用于大多数题目!
反例:求树上数据的中位数 -> 局部中位数无法推出全局中位数,故不可行!
七、其他题型
1、最低公共祖先
Q:给定两个在同一棵树上的二叉树节点node1和node2,找到他们的最低公共祖先;

思路:
(1)定义集合set保存二叉树中所有的连接关系;
(2)接着定义集合set1,根据set中的信息,从o1节点往上找,找出从o1到根节点的路径;
(3)同理,让o2根据set中的信息往上找,当o2达到的节点包含在集合set1中时,该节点就是他们的最低公共祖先。


优化思路:先分类讨论,本题中共两种情况(分别为下图的黄色标记和蓝色标记):
Case1:o1、o2在同一条路径上(o1是o2的lca或者o2是o1的lca);
Case2:o1、o2不在同一条路径上(o1与o2不互为lca);

代码:

上述代码经过了多轮优化,所以直接看看不懂很正常!!
关键点:第二个 if 仅针对case2成立(汇聚点);按递归序扫描时,遇到o1或o2就会一直返回。
2、后继节点
Q:从结构上寻找后继节点(中序遍历中,某节点的下一个节点叫做后继节点);

关键点:由于给出了parent指针,故需要根据结构进行优化;
分类讨论:1)该节点有右树;2)该节点无右树

代码实现:


注意,getSuccessorNode函数中,else分支中同时考虑了节点无右树的两种情况!
3、序列化与反序列化
序列化和反序列化是将数据结构(在本例中是二叉树)转换为可存储或传输的格式的过程,并能够恢复其原始结构的技术。具体来说:
-
序列化:将二叉树转化为一个可以存储(如存入文件)或传输(如通过网络传输)的格式,通常是字符串或数组。【序列化后的数据结构应该包含足够的信息,以便在反序列化时能够恢复原来的二叉树结构。】
-
反序列化:从序列化的格式中恢复出原始的二叉树结构。
-
序列化时,我们可以使用前序遍历(根-左-右)或后序遍历(左-右-根)等遍历方法来对二叉树进行遍历,并将遍历结果转化为字符串。例如,我们可以用“
NULL”标识空节点,使用逗号分隔节点值。 -
反序列化时,我们通过序列化时得到的字符串恢复出二叉树的结构。根据序列化时的规则逐步重建树的每个节点。
代码:
#include <bits/stdc++.h>
using namespace std;
// 定义二叉树节点结构体
struct Node {
int val;
Node* left;
Node* right;
Node(int v) : val(v), left(nullptr), right(nullptr) {}
};
// 序列化二叉树的函数
string serialize(Node* root) {
if (root == nullptr) {
return "NULL,"; // 使用"NULL"标记空节点
}
return to_string(root->val) + "," + serialize(root->left) + serialize(root->right);
}
// 反序列化二叉树的函数
Node* deserializeHelper(istringstream& ss) {
string val;
getline(ss, val, ','); // 读取以逗号分隔的节点值
if (val == "NULL") {
return nullptr; // 如果是空节点,返回nullptr
}
Node* node = new Node(stoi(val)); // 创建当前节点
node->left = deserializeHelper(ss); // 递归反序列化左子树
node->right = deserializeHelper(ss); // 递归反序列化右子树
return node;
}
Node* deserialize(const string& data) {
istringstream ss(data);
return deserializeHelper(ss);
}
// 用于打印树的前序遍历
void preorder(Node* root) {
if (root == nullptr) return;
cout << root->val << " ";
preorder(root->left);
preorder(root->right);
}
int main() {
// 构造一棵示例二叉树
Node* root = new Node(10);
root->left = new Node(8);
root->right = new Node(12);
root->left->left = new Node(4);
root->left->right = new Node(9);
root->right->left = new Node(11);
root->right->right = new Node(14);
cout << "Preorder traversal of the tree: ";
preorder(root);
cout << endl;
// 序列化二叉树
string serialized = serialize(root);
cout << "Serialized tree: " << serialized << endl;
// 反序列化二叉树
Node* deserializedRoot = deserialize(serialized);
cout << "Preorder traversal of deserialized tree: ";
preorder(deserializedRoot);
cout << endl;
return 0;
}4、折纸面试题(微软)

动手实践后可知,可以抽象为二叉树结构:

代码实现:(二叉树模拟+中序遍历)

上述代码空间复杂度 O(N) 级别,直接计算长度为 2^(N-1) 为 O(2^N) 级别!节省了很多的空间!
























 399
399

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








