最全卷积总结篇（分组、深度可分离、空洞、转置等）

胡乱儿起个名

已于 2025-04-18 23:39:23 修改

阅读量3k

点赞数 33

分类专栏： PyTorch框架深度学习基础机器学习文章标签： pytorch 深度学习人工智能 cnn

于 2024-11-26 21:52:51 首次发布

本文链接：https://blog.youkuaiyun.com/qq_44815135/article/details/144030014

版权

1.普通卷积

1.1 卷积计算过程

在这里插入图片描述

1.2 多输入通道计算过程

在这里插入图片描述

1.3 多输出通道计算过程

在这里插入图片描述

2. 1x1卷积

2.1. 1×1卷积

1×1 卷积，与标准卷积完全一样，唯一的特殊点在于卷积核的尺寸是1×1 ，也就是不去考虑输入数据局部信息之间的关系，而把关注点放在不同通道间。当输入矩阵的尺寸为3×3 ，通道数也为3时，使用4个1×1卷积核进行卷积计算，最终就会得到与输入矩阵尺寸相同，通道数为4的输出矩阵，如图所示。

在这里插入图片描述

2.2. 1×1 卷积的作用

实现信息的跨通道交互与整合。考虑到卷积运算的输入输出都是3个维度（宽、高、多通道），所以1×1卷积实际上就是对每个像素点，在不同的通道上进行线性组合，从而整合不同通道的信息。
对卷积核通道数进行降维和升维，减少参数量。经过1×1 卷积后的输出保留了输入数据的原有平面结构，通过调控通道数，从而完成升维或降维的作用。
利用1×1 卷积后的非线性激活函数，在保持特征图尺寸不变的前提下，大幅增加非线性。

3.分组卷积

3.1 什么是分组卷积？

分组卷积（Group Convolution）是一种卷积操作方式，它最早在AlexNet中引入，并在深度学习中被广泛使用，尤其是在高效模型设计（如MobileNet和ResNeXt）中。分组卷积通过将输入特征通道分为若干组，并在每组内单独进行卷积操作，可以减少计算复杂度和参数量，同时有效利用模型的结构特性。
在这里插入图片描述
分组卷积的工作原理

通道分组：输入特征图的通道图为C_in,输出特征图的通道数为C_out,将每组的C_in和C_out分为G组，每组的通道数为C_in/G和C_out/G。
组内卷积：每组的输入通道仅与对应组的卷积核进行卷积，组间相互独立。
输出拼接：所有组的卷积输出特征图按照通道维度拼接，形成最终输出。

如果分组=1，分组卷积退化为普通的全通道卷积；
如果分组=输入通道数,分组卷积变为深度卷积。

3.2 分组卷积优势

在这里插入图片描述

4.深度可分离卷积

4.1什么是深度可分离卷积？

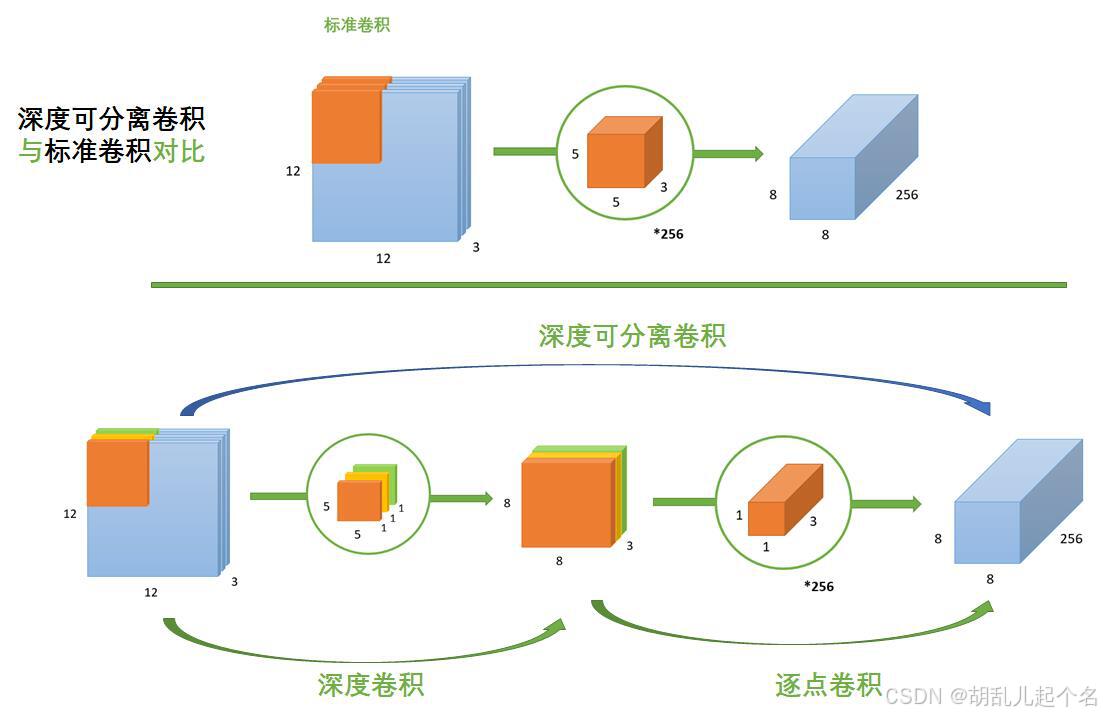
深度可分离卷积将传统卷积操作拆分成两个步骤：

深度卷积：每个输入通道都使用独立的卷积核进行卷积。
逐点卷积：使用 1x1 卷积核对深度卷积的输出进行跨通道的融合。

在这里插入图片描述

4.2 深度可分离卷积的计算量

在这里插入图片描述

4.3 与普通计算量的比较

在这里插入图片描述

5.空洞卷积

空洞卷积（Dilated Convolution），也叫膨胀卷积，是一种特殊的卷积操作，主要用于扩大感受野，同时保持计算效率。它通过在卷积核采样点之间插入空隙（即膨胀率），有效地提升了卷积操作对全局特征的捕获能力，而不增加参数量或计算成本。
在这里插入图片描述

5.1 什么是感受野？

下图是一个普通卷积的过程，卷积核大小为3×3，步长s=1。可以发现，所得特征图中一个1×1像素区域（灰绿色）对应了原图中的3×3大小的区域，这就是3×3大小卷积核的感受野。
在这里插入图片描述我们再来看，当我们对刚刚得到的特征图（橙色）再经过一次3×3卷积，如下图所示：

在这里插入图片描述很显然，此时最后一层特征图中一个1×1像素区域（青蓝色）对应了橙色特征图中的3×3大小的区域，这也是3×3大小卷积核的感受野。
那么，现在我将上述两步放在一起，如下图所示：

在这里插入图片描述那么请问，此时最后一层特征图中一个1×1像素区域（青蓝色）对应原图多少尺寸大小的区域呢？答案是5×5，因为青蓝色像素感受野包含了整个橙色的区域，而整个橙色区域的感受野正是下方5×5区域大小的范围。

通过上文叙述，我们知道了感受野是怎么计算的了，下面给出计算感受野的公式, k_d是空洞卷积核大小，kernel_size 是原卷积核大小

 k_d = (kernel_size - 1) * dilation_rate + 1 
 F_i = (F_i - 1) * stride + k_d

5.2 空洞卷积

优势：它能够在不进行下采样操作（如使用pooling层）的情况下，保持或增大特征图的尺寸，同时增加感受野（receptive field）的大小，从而能够在图像分割等任务中捕获更广泛的信息。
在这里插入图片描述看图的时候，你可以忽略红点，红点只是想说明空洞卷积时卷积的样子。如果非要理解，可以这样来看，F0层到F1层，由于是正常卷积，红点就是 3×3的，感受野也是 3×3。F1层到F2层，空洞卷积，所以我们会发现红点中间都隔了一个0值，又由于用每个红点卷积F1层时感受野都是3×3的，所以浅绿色在外层又多了一圈变为了 7×7。F2层到F3层，红点中间隔了3个，每个红点由覆盖了F2层的 7×7，所以感受野就变为了15×15。

(a) F1 是通过从 F0 应用一个空洞率为 1 的空洞卷积产生的；F1 中的每个元素具有 3×3 的感受野。

(b) F2 是通过从 F1 应用一个空洞率为 2 的空洞卷积产生的；F2 中的每个元素具有 7×7 的感受野。

再解释一遍，假设步长均为1。假设我们有图(a)这样一个输入层（白色格子），首先应用一个普通的 3×3卷积核（空洞率为1）卷积到F1层，那么显然F1层的每个值的感受野都是3×3（图a中的浅绿色）。从F1层到F2层，我们应用一个空洞率为2的3×3卷积核，那么F2层的每个值的感受野，变为了7×7（图b中的浅绿色）。从F2层到F3层，我们应用一个空洞率为4的3×3卷积核，那么F3层的每个值的感受野，变为了15×15（图c中的浅绿色）。感受野在指数级增长：空洞率又2变4，视野也由7变为了15。

重要的是，尽管感受野在指数级地增长（从 3×3 到 7×7 再到 15×15），但每一层与之相关的参数数量是恒定的。这是因为空洞卷积只是通过在卷积核的元素之间插入零来增加感受野，而不是增加卷积核的实际大小或数量。这种特性使得空洞卷积在需要大感受野但又要控制模型复杂性的任务中特别有用，例如图像分割、目标检测等。通过系统地调整空洞率，可以在不增加计算成本的情况下有效地捕获多尺度的上下文信息。