本文详细解析了《混沌映射与比特重组的图像加密》一文中的加密算法，包括置乱和扩散两个阶段。首先，通过Tent混沌系统进行像素的行和列置乱，接着使用可逆的Henon映射进行进一步的像素位置变换。在解密过程中，通过逆操作还原图像。文章还指出了原文中的一些错误和修正方法。
索引
传送门
- 文献原文可前往其收录处《混沌映射与比特重组的图像加密》.
- 原文算法的实现可以参见博文《《混沌映射与比特重组的图像加密》（平萍等）一文的算法实现（基于Matlab）》.
- 对算法背后一些理论的分析可以参见博文《《混沌映射与比特重组的图像加密》（平萍等）一文的算法分析》.
- 对原文算法的改进可以参见博文《《混沌映射与比特重组的图像加密》（平萍等）一文的算法改进和展望》.
- 对算法及其改进形式的仿真实验可以参见博文《《混沌映射与比特重组的图像加密》（平萍等）一文的仿真实验 (基于Matlab)》.
- 对算法的性能分析可以参见博文《《混沌映射与比特重组的图像加密》（平萍等）一文的性能分析（一）-- 敏感性分析 (基于Matlab)》 以及 《《混沌映射与比特重组的图像加密》（平萍等）一文的性能分析（二）-- 相关性, 安全性强度, 计算用时分析 (基于Matlab)》.
原文中的加密算法步骤 (原文只给出加密算法)
第1阶段置乱
(1) 选取一幅大小为 M × N M\times N M×N的灰度级数字图像, 计算图像中像素值的总和记作 s s s, 然后利用式(1), (2)分别计算出Tent混沌系统的控制参数 μ \mu μ和Tent混沌系统初始迭代的次数 k k k, 即
μ = 2 s / M × N × 255 , (1) \mu ={
{2}^{
{s}/{M\times N\times 255}\;}}, \tag{1} μ=2s/M×N×255,(1)
k = s m o d 10 3 + 10 3 . (2) k=s\text{ }\bmod {
{10}^{3}}+{
{10}^{3}}. \tag{2} k=s mod103+103.(2)
式中 s / ( M × N × 255 ) {s}/{\left( M\times N\times 255 \right)}\; s/(M×N×255)的结果不取整.
注 Tent混沌系统的系统方程定义为
x ( n + 1 ) = { μ x ( n ) , 0 < x ( n ) ≤ 0.5 , μ ( 1 − x ( n ) ) , 0.5 < x < 1. x\left( n+1 \right)=\left\{ \begin{aligned} & \mu x\left( n \right),\text{ }0<x\left( n \right)\le 0.5, \\ & \mu \left( 1-x\left( n \right) \right),\text{ }0.5<x<1. \\ \end{aligned} \right. x(n+1)={
μx(n), 0<x(n)≤0.5,μ(1−x(n)), 0.5<x<1.
即
x ( n + 1 ) = μ × min { x ( n ) , 1 − x ( n ) } , 0 < x ( n ) < 1. x\left( n+1 \right)=\mu \times \min \left\{ x\left( n \right),\text{ }1-x\left( n \right) \right\},\text{ }0<x\left( n \right)<1. x(n+1)=μ×min{
x(n), 1−x(n)}, 0<x(n)<1.
要求 x ( n ) ∈ ( 0 , 1 ) , μ ∈ ( 0 , 2 ) x\left( n \right)\in \left( 0,1 \right),\text{ }\mu \in \left( 0,2 \right) x(n)∈(0,1), μ∈(0,2). 原文关于上述方程的表述存在印刷失误. 当 μ > 1 \mu >1 μ>1时, 系统处于混沌状态.
由式(1), 当明文图像为纯黑图像时, μ = 2 0 = 1 \mu ={
{2}^{0}}=1 μ=20=1, 当明文图像为纯白图像时, μ = 2 1 = 2 \mu ={
{2}^{1}}=2 μ=21=2, 而当明文图像介于纯黑与纯白之间, 则有 μ ∈ ( 1 , 2 ) \mu \in \left( 1,2 \right) μ∈(1,2)符合条件. 在这个前提下, 只要控制初始输入的密钥 0 < x 0 < 1 0<{
{x}_{0}}<1 0<x0<1, 则后续的 ∀ n ∈ Z > 0 \forall n\in {
{\mathbb{Z}}_{>0}} ∀n∈Z>0, 均有 x ( n ) ∈ ( 0 , 1 ) x\left( n \right)\in \left( 0,1 \right) x(n)∈(0,1).
(2) 将像素矩阵中每个像素转换成 8 8 8位二进制数. 例如数 123 123 123转换成8位二进制是 01111011 01111011 01111011.
(3) 输入初始密钥 x 0 { {x}_{0}} x0, 并根据步骤(1)求出的控制参数 μ \mu μ, Tent混沌系统进行 k k k次迭代, 消除初态效应的影响.
(4) Tent混沌系统继续迭代 M M M次, 由此产生长度为 M M M的混沌序列 E = { e 1 , e 2 , ⋯ , e M } E=\left\{ { {e}_{1}},{ {e}_{2}},\cdots ,{ {e}_{M}} \right\} E={ e1,e2,⋯,eM}, 产生的混沌序列的值均在 0 0 0到 1 1 1之间.
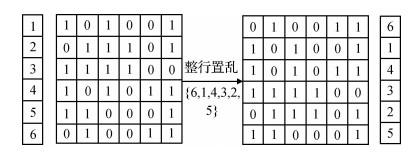
(5) 将步骤(4)生成的序列 E E E按升序排序, 从而得到一个位置向量 P E = { p 1 E , p 2 E , ⋯ , P M E } { {P}^{E}}=\left\{ { {p}_{1}}^{E},{ {p}_{2}}^{E},\cdots ,{ {P}_{M}}^{E} \right\} PE={ p1E,p2E,⋯,PME}, 利用生成的位置向量 P E { {P}^{E}} PE, 对已经转成比特的数字图像矩阵进行整行置乱. 比如任意序列 { 0.3 , 0.7 , 0.5 , 0.4 , 0.8 , 0.2 } \left\{ 0.3,\text{ }0.7,\text{ }0.5,\text{ }0.4,\text{ }0.8,\text{ }0.2 \right\} { 0.3, 0.7, 0.5, 0.4, 0.8, 0.2}, 将该序列按升序进行排序后得到有序序列是 { 0.2 , 0.3 , 0.4 , 0.5 , 0.7 , 0.8 } \left\{ 0.2,\text{ }0.3,\text{ }0.4,\text{ }0.5,\text{ }0.7,\text{ }0.8 \right\} { 0.2, 0.3, 0.4, 0.5, 0.7, 0.8}, 则相应的位置序列就是 { 6 , 1 , 4 , 3 , 2 , 5 } \left\{ 6,\text{ }1,\text{ }4,\text{ }3,\text{ }2,\text{ }5 \right\} { 6, 1, 4, 3, 2, 5}. 下图为采用该位置序列的一个整行置乱示意图.
(6) Tent混沌系统继续迭代 8 × N 8\times N 8×N次, 由此产生的长度为 8 × N 8\times N 8×N的混沌序列 F = { f 1 , f 2 , ⋯ , f M } F=\left\{ {
{f}_{1}},{
{f}_{2}},\cdots ,{
{f}_{M}} \right\} F={
f1,f2,⋯,fM}, 将序列 F F F按升序排序之后得到相应的位置向量 P F = { p 1 F , p 2 F , ⋯ , p M F } {
{P}^{F}}=\left\{ {
{p}_{1}}^{F},{
{p}_{2}}^{F},\cdots ,{
{p}_{M}}^{F} \right\} PF={
p1F,p2F,⋯,pMF}, 利用 P F {
{P}^{F}} PF对数字图像矩阵进行整列置乱.
第2阶段置乱
(1) Tent混沌系统继续迭代 M × N M\times N M×N次, 由此产生的长度为 M × N M\times N M×N的混沌序列 R = { r 1 , r 2 , ⋯ , r M × N } R=\left\{ {
{r}_{1}},{
{r}_{2}},\cdots ,{
{r}_{M\times N}} \right\} R={
r1,r2,⋯,rM×N}.
(2) 将第1阶段得到的置乱矩阵从左到右分成8个 M × N M\times N M×N的比特矩阵, 对 8 8 8个矩阵分别使用Henon映射
{ x ( n + 1 ) = 1 − a x ( n ) 2 + y ( n ) m o d N , y ( n + 1 ) = b x ( n ) + c m o d N , (3) \left\{ \begin{aligned} & x\left( n+1 \right)=1-ax{
{\left( n \right)}^{2}}+y\left( n \right)\text{ }\bmod N, \\ & y\left( n+1 \right)=bx\left( n \right)+c\text{ }\bmod N, \\ \end{aligned} \right. \tag{3} {
x(n+1)=1−ax(n)2+y(n) modN,y(n+1)=bx(n)+c modN,(3)
进行置乱, 式(3)中控制参数 a i ( i = 1 , 2 , ⋯ , 8 ) {
{a}_{i}}\left( i=1,2,\cdots ,8 \right) ai(i=1,2,⋯,8)为
a i = C e i l i n g ( f N / 2 + i × 10 14 ) m o d 2 8 , {
{a}_{i}}=Ceiling\left( {
{f}_{N/2+i}}\times {
{10}^{14}} \right)\text{ }\bmod {
{2}^{8}}, ai=Ceiling(fN/2+i×1014) mod28,
c i = C e i l i n g ( f N / 2 + i 2 × 10 14 ) m o d 2 8 . {
{c}_{i}}=Ceiling\left( {
{f}_{N/2+i}}^{2}\times {
{10}^{14}} \right)\text{ }\bmod {
{2}^{8}}. ci=Ceiling(f
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
