关于堆（heap）

说在前面

我第一次接触堆这个东西是在做堆排序的时候。这玩意还不错，难度也不大，可以用的地方很多，值得玩一玩。

前置知识：

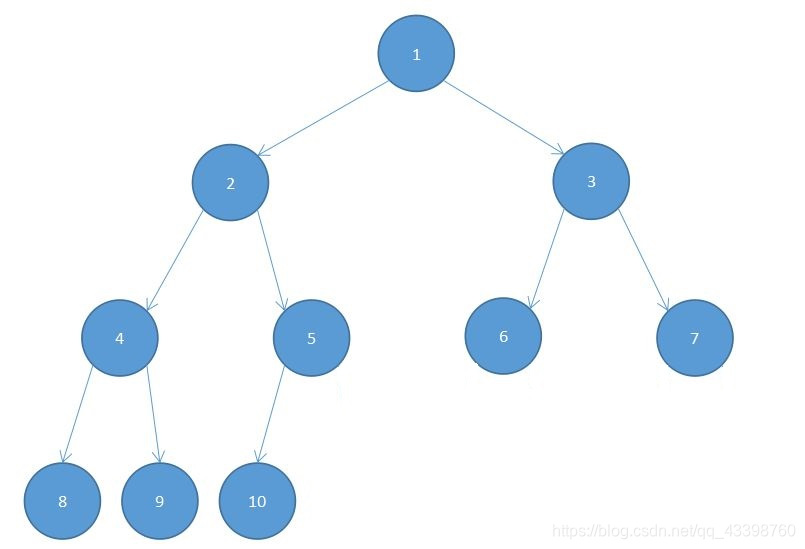
完全二叉树

完全二叉树 ，顾名思义是一种二叉树就是说 （假设树根深度为1 ）深度为k的二叉树 ，第1至第k-1层的结
点都是满的，也就是说 ，如果一颗二叉树满足第i(1<=i<=K-1)层的结点数为2 * i-1  ，0<第K层的结点数
<=2 * k-1  ，并且最下面一层的结点都集中在该层最左边的若干位置 ，那么它就是一颗完全二叉树。

like this:

堆的性质及其基本操作：

堆的性质

1.编号为i的结点的左二子的编号为2 * i  ，右儿子编号为2 * i + 1  ，父结点编号为i / 2 （假设有）

2.n个结点的堆的高度为log2(n + 1)的对数

3.h[i] <= h[2 * i], h[i] <= h[2 * i + 1] （或者 h[i] >= h[2 * i], h[i] >= h[2 * i + 1] ）ps:前面那个是小
根堆 ，即h[1]是最小值 ；而后者为大根堆 ，即h[1]是最大值。

 

基本操作

1.上浮（up）

void up(int x) { //h[x]上浮
	while(x > 1 && h[x] < h[x >> 1]) {
		swap(h[x], h[x >> 1]);
		x >>= 1;
	}
}

 

2.下沉（down）

void down(int x) { //h[x]下沉，len是堆中元素个数
	int y = x << 1;
	while(y <= len) {
		if(y + 1 <= len && h[y + 1] < h[y]) y++;
		if(h[y] < h[x]) {
			swap(h[x], h[y]);
			x = y;
			y = x << 1;
		} else break;
	}
}

3.读入（insert）

void insert(int x) {
	h[++len] = x;
	up(len);
}

4.删除（delete）

void del(int x) {  //删除元素h[x]
	h[x] = h[len--];
	up(x);
	down(x);
}

下面放一个模板（小根堆）：

#include<bits/stdc++.h>
using namespace std;
int n, k;
int a[100010], h[100010];
int b[100010];
int cnt, len;

void up(int x) {
	while (x > 1 && h[x] < h[x >> 1]) {
		swap(h[x], h[x >> 1]);
		x >>= 1;
	}
}

void down(int x) {
	int y = x << 1;
	while (y <= len) {
		if (y + 1 <= len && h[y + 1] < h[y]) y++;
		if (h[y] < h[x]) {
			swap(h[x], h[y]);
			x = y;
			y = x << 1;
		}
		else break;
	}
}

void insert(int x) {
	h[++len] = x;
	up(len);
}

int solve() {
	int d = h[1];
	h[1] = h[len--];
	down(1);
	return d;
}

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		scanf("%d", &a[i]);
		insert(a[i]);
	}
	for (int i = 1; i <= n; i++) {
		cout << solve() << " ";
	}
}
/*
13
19 17 16 12 9 15 1 2 11 7 3 10 14
*/

几个题目：

入门OJ1551 合并果子

入门OJ1552 合并果子2

入门OJ2104 ksum