C++手写非线性优化方法: GN & LM & DL，对比测试

置顶 已于 2023-09-18 10:55:14 修改
阅读量1.5k 收藏 18
点赞数 4
分类专栏： 0_1SLAM 文章标签： c++ 机器人 自动驾驶
于 2022-09-12 20:59:40 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_42911741/article/details/126798707
版权

0、状态估计 

        对机器人状态估计：输入u，观测z，估计状态x ---> 条件概率P(x|z,u) ----------(贝叶斯)-------> 后验概率P(x|Z) =  P(Z|x) * P(x) / P(Z) (后验=似然*先验) ---> (后验最大化，似然就得最大化，变作求x的最大似然估计MLE)；

        MLE：在什么状态下，最可能产生现在的观测数据；

        ====> 对运动方程/观测方程作高斯分布，取其负对数分析 ---> 误差的二范数最小问题(非线性最小二乘问题) ---> 求解方法(1-极值点，2-梯度下降)；
梯度下降：在函数求导复杂时(不好解出极值点)，寻找一个增量，直到增量很小时，使目标函数达到一个极小，就算收敛；

常用的矩阵求导法则：

        Y = AX                ==>                Y对X求导等于A^{T}

        Y = X^{T}AX          ==>                Y对X求导等于2AX

        A^{2} = A^{T}A

1阶梯度法：泰勒展开保留1阶项（最速下降法）

        \Delta x^{*} = -J(x)^{T}，最优梯度\Delta x^{*}直接用雅克比矩阵反向传播，我们还需要该方向上取一个步长 \lambda，贪心下降，呈锯齿下降，一般记为h_{sd}；
2阶梯度法：泰勒展开保留2阶项（牛顿法）

        H\Delta x = -J(x)^{T}，大规模矩阵非常难计算H；

其中，一二阶梯度法，是对f(x)^{2}为目标函数进行泰勒展开；雅克比矩阵J：一阶导，海塞矩阵H：二阶导 ；

更常用的方法：高斯牛顿法、列文伯格-马夸尔特法(阻尼牛顿法)、Dog-Leg等。

一、高斯牛顿法

        对f(x)展开，并不是对f(x)^{2}展开：f(x+\Delta x) \approx f(x) + J(x)\Delta x，接下来就是寻找下降矢量\Delta x，使得 \left \| f(x+\Delta x) \right \|^{2}达到最小，构建出的最小二乘问题：

\Delta x^{*} = arg\ min_{\Delta x}\frac{1}{2}\left \| f(x) + J(x)\Delta x \right \|^{2}

上述函数对\Delta x进行求导：

J(x)^{T}J(x)\Delta x = -J(x)^{T}f(x)

记H(x) = J(x)^{T}J(x), g(x) = -J(x)^{T}f(x)，得到高斯牛顿方程：

H(x)\Delta x = g(x)

求解上述的线性方程，需要假设H矩阵是可逆矩阵，J^{T}J只是半正定，否则求解出来的增量稳定性较差；每次迭代需要计算：x_{k} = x_{k-1} + \Delta x, J(x_{k}), f(x_{k})等；

简单优化：可以在每次得出的增量前，乘以一个因子，去控制增量过剧烈的病变。

Code：

// gn.cpp
// 估计函数  y(x) = exp( a*x*x + b*x + c ) 
int main() {
	std::vector<double> x_set, y_set;
	double a = 1, b =2 , c = 1;			// 待估计参数

	srand(time(NULL));
	double seed = (rand() % (10-1)) + 1; 
	for (int i = 1; i<= Sample_NUM; ++i) {

		// x样本
		double x = (double)i/100.0;
		x_set.push_back(x); 

		// Define random generator with Gaussian distribution
		double mean = 0.0;		//均值
		// double stddev = (double)seed/10;	//标准差0-1
		double stddev = 1.0;//标准差
		std::default_random_engine generator; 
		std::normal_distribution<double> gauss(mean, stddev);

		// y样本   // Add Gaussian noise
		double y =  exp( a*x*x + b*x + c )  + gauss(generator);

		y_set.push_back(y);
	}
        // // Output the result, for demonstration purposes
	// std::copy(begin(x_set), end(x_set), std::ostream_iterator<double>(std::cout, " "));
        // std::cout << "\n";
        // std::copy(begin(y_set), end(y_set), std::ostream_iterator<double>(std::cout, " "));
        // std::cout << "\n";

	// gn 算法
	static double aft_a = 0.0, aft_b = 0.0, aft_c = 0.0;
	Eigen::Vector3d delta_abc;
	Eigen::MatrixXd Jacb_abc, error_i;
	Eigen::Matrix3d H; 
	Eigen::Vector3d g;
	// Eigen::MatrixXd lastCost, curCost;
	double lastCost, curCost;

	if (x_set.size() != Sample_NUM || y_set.size() != Sample_NUM) {

		std::cerr << "data error!\n";
		return -1;
	}

	int iteratorNum = 100;	// 迭代次数
	for(int i = 1; i<=iteratorNum; i++) {
		for (int i = 0; i< Sample_NUM; ++i) {
			Jacb_abc.resize(Sample_NUM, 3);
			error_i.resize(Sample_NUM, 1);

			double y_est = exp( aft_a * x_set.at(i) * x_set.at(i) + 	\
													aft_b * x_set.at(i) + aft_c);
			// 雅克比  对待优化变量的偏导 
			Jacb_abc(i,0) =   -x_set.at(i) * x_set.at(i) * y_est;
			Jacb_abc(i,1) =   			    -x_set.at(i) * y_est;
			Jacb_abc(i,2) = 					    -1.0 * y_est;
		
			// 误差
			error_i(i, 0) = y_set.at(i) - y_est;
		}	
		// 计算增量方程 H * delta_? = g	
		H = Jacb_abc.transpose() * Jacb_abc;		// 计算H
		g = -Jacb_abc.transpose() * error_i; 		// 计算g 
		delta_abc = H.ldlt().solve(g); 
		
		// 误差norm
		curCost = (error_i.transpose() * error_i)(0,0);

		if (i%10==0)
			std::cout << "当前迭代次数: " << i << "/" << iteratorNum << "     当前总误差: " << curCost  << std::endl;

		if ( isnan(delta_abc(0)) || isnan(delta_abc(1)) || isnan(delta_abc(2)))
			continue; 
	
		// 判断是否提前收敛 增量是否足够小
		//if (abs(delta_abc[0]) < 0.00001 && abs(delta_abc[1]) < 0.00001 && abs(delta_abc[2]) < 0.00001) {
		//	break;
		//}
			
		// 更新增量
		aft_a += delta_abc[0];
		aft_b += delta_abc[1];
		aft_c += delta_abc[2];
	}
	std::cout << "真实abc: " << a << " " << b << " " << c << std::endl;
	std::cout << "迭代结束! \n" << "a: " << aft_a << "\nb: " << aft_b 
							<< "\nc: " << aft_c << std::endl;
	return 0;
}

上述代码的迭代结果：70次才收敛

          这里我用g2o的GN算法也跑了一下（视觉14讲的例程），发现收敛不了，是什么原因（和我手写GN算法测试的样本数据里的高斯噪声均值、方差设置都一样，知道的小伙伴可以告诉我一下=_=），之后我换成g20的lm、dl都可以收敛。。。

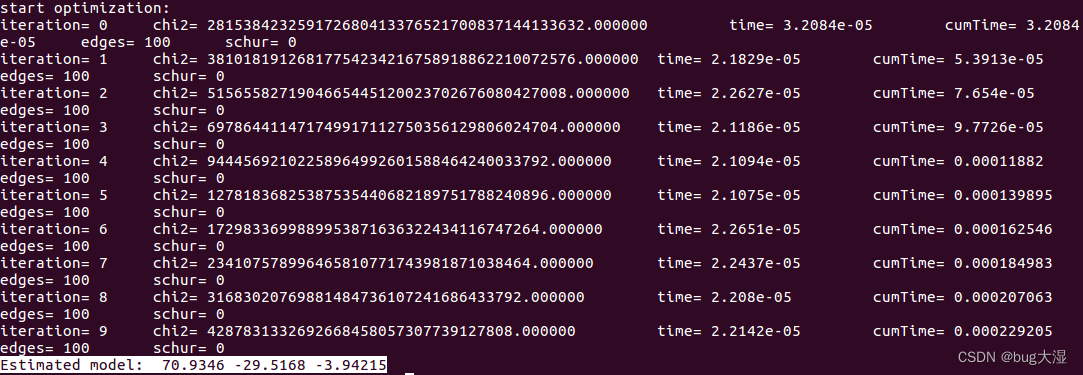
         望知道原因的小伙伴指点以下，跪谢！！！（高斯牛顿陷入了局部极值，对初值十分依赖，好的初值可以让摆脱掉陷入局部的问题）

补充：拉氏乘法在优化问题的作用

        在下面介绍的LM中，会采用拉氏乘法将不等式约束问题转化为无约束的优化问题：形如：求f(x)，带约束h(x) <= 0下的极值. 同样定义拉格朗日函数: F(x,delta) = f(x)+delta*h(x);

        首先看目标函数，f(x)在无约束条件下的最优点，显然要么在h(x)<=0的区域内，要么在h(x)>0的区域内;

        若f(x)在无约束条件下的最优点在h(x)<=0区域内，则约束条件h(x)<=0不起作用（即可直接求min f(x)，得到的结果必然满足h(x)<=0），相当于delta=0;

        若f(x)在无约束条件下的最优点不在h(x)<=0区域内，则f(x)在约束条件下的最优点必然在h(x)<=0区域边界，即在边界h(x)=0上。此类情形类似于等式约束，但此时梯度▽f(x*)和▽h(x*)的方向相反（梯度方向是函数值增大最快的方向），即存在delta>0，使▽f(x*)+delta*▽h(x*)=0；

        综上所述，必有delta*g(x) = 0。所以原不等式约束问题就转化为：min F(x,delta) , s.t. g(x)<=0,  delta>=0, delta*g(x)=0. 上面的约束条件即为KKT条件。

二、列文伯格-马夸尔特法

        考虑对每次求得的增量\Delta x进行一个信赖区域的约束，一定层度上解决了高斯牛顿H矩阵出现病态的问题；信赖区域的控制因子（用实际模型与近似模型的比值，实际上就是判断这个泰勒近似的可信度）：

\rho = \frac{f(x+\Delta x)-f(x)}{J(x)\Delta x}，                 \left \| D\Delta x \right \|^{2}\leq \mu

        注意：\rho \approx 1，近似可靠；\rho \gg 1，实际模型下降更大，可以放大增量范围；\rho \ll 1，近似模型下降大，需要缩小增量可信度范围；一般，\rho > 3/4，则\mu = 2\mu，\rho < 1/4，则\mu = 0.5\mu；

        用拉格朗日乘子将不等式约束问题转化为无约束问题，\lambda为拉格朗日乘子：

\Delta x^{*} = arg \ min_{\Delta x}\frac{1}{2}\left \| f(x)+J(x)\Delta x \right \|^{2}+\frac{\lambda }{2}\left \| D\Delta x \right \|^{2}

同样对增量求导得：

(H(x)+\lambda D^{T}D)\Delta x = g(x)

         D为非负数对角阵：可以取单位矩阵或者取J^{T}J对角线元素的平方根；分析上式：\lambda较小时，增量由H矩阵决定，类似高斯牛顿；\lambda较大时，D取为I，类似最速下降；

 Code：

        int iteratorNum = 100;	// 迭代次数
	for(int i = 1; i<=iteratorNum; i++) {

		for (int j = 0; j< Sample_NUM; ++j) {		// 构造方程
			Jacb_abc.resize(Sample_NUM, 3);
			error_i.resize(Sample_NUM, 1);

			double y_est = exp( aft_a * x_set.at(j) * x_set.at(j) + 	\
													aft_b * x_set.at(j) + aft_c);
			// 雅克比  对待优化变量的偏导 注意真实的J应该是
			Jacb_abc(j,0) =   -x_set.at(j) * x_set.at(j) * y_est;
			Jacb_abc(j,1) =   			    -x_set.at(j) * y_est;
			Jacb_abc(j,2) = 					    -1.0 * y_est;
		
			// 误差
			error_i(j, 0) = y_set.at(j) - y_est;
		}	
		// 计算增量方程 H * delta_? = g	
		H = Jacb_abc.transpose() * Jacb_abc;		// 计算H
		g = -Jacb_abc.transpose() * error_i; 		// 计算g
	
		// 误差平方和
		curSquareCost = 1.0f/2*(error_i.transpose() * error_i)(0,0);
		// std::cout << curSquareCost << std::endl;	

		// 计算初始的u
		// 初值比较好，t取小；初值未知，t取大
		// 去对角线最大元素作为初值
		static bool isFirstStart = true;
		if (isFirstStart) {
			
			double diag_max_element = 0.0;
			for (int m = 0; m<H.rows(); ++m ) {
				if (H(m,m) >= diag_max_element) {
					diag_max_element = H(m,m);
				}
			}
			double t = 1.0;		//1e-6  1e-3  或者 1.0
			u = t * diag_max_element;
			isFirstStart = false;
		}

		// 计算增量方程 （H + namDa*D_pow2） * delta_? = g
		Eigen::Matrix3d D_pow2 = Eigen::Matrix3d::Identity();
		delta_abc = (H + u*D_pow2).ldlt().solve(g); 

		if ( isnan(delta_abc(0)) || isnan(delta_abc(1)) || isnan(delta_abc(2)))
			continue; 
	
		// 判断是否提前收敛 增量是否足够小
		double delta_h = delta_abc.transpose() * delta_abc;
		if (delta_h < 1e-8) {  
			std::cout << "真实abc: " << a << " " << b << " " << c << std::endl;
			std::cout << "迭代结束! \n" << "a: " << aft_a << "\nb: " << aft_b 
							<< "\nc: " << aft_c << std::endl;
			return 0;
		}

		// 求一阶泰勒近似度
		error_sum_aft.resize(Sample_NUM, 1);
		for (int k = 0; k<Sample_NUM; k++) {
			error_sum_aft(k,0) = y_set.at(k) - exp( (aft_a+delta_abc(0)) * x_set.at(k) * x_set.at(k) + 	\
													(aft_b+delta_abc(1)) * x_set.at(k) + (aft_c+delta_abc(2)) );
		}	
		curSquareCost_aft = 1.0/2*(error_sum_aft.transpose() * error_sum_aft)(0,0);

		// Eigen::MatrixXd L0_Ldelta = -delta_abc.transpose() * Jacb_abc.transpose() * error_i - 1.0f/2 * delta_abc.transpose() * Jacb_abc.transpose() * Jacb_abc * delta_abc;
		Eigen::MatrixXd L0_Ldelta = 1.0f/2 * delta_abc.transpose() * ( u*delta_abc + g);      
		
		taylar_similary = (curSquareCost-curSquareCost_aft) / L0_Ldelta(0,0);

		if (taylar_similary>0) { 	// 近似可用 
			// 更新增量
			aft_a += delta_abc(0);
			aft_b += delta_abc(1);
			aft_c += delta_abc(2);
			// 更新u
			u = u * std::max<double>(1.0/3, 1-pow(2*taylar_similary-1, 3));
			v = 2.0;
			
		}else{
			// 近似不可用  采用一阶梯度
			u = v*u;
			v = 2*v;		
		}

		if (i%1==0) 
		{
			std::cout << "   泰勒近似: " << taylar_similary << std::endl;
			std::cout << "   本次增量: " << delta_abc.transpose() << std::endl;
			std::cout << "当前迭代次数: " << i << "/" << iteratorNum << "     当前总误差: " << curSquareCost << std::endl<< std::endl;
		}

	}

上述代码的迭代结果：

可以看到迭代了21次就收敛到了不错的数据；并且一定程度上解决GN的问题；

三、狗腿Dog-Leg

        狗腿法是置信区域方法的一种。

        考虑最速下降的优化方式，求其步长：f(x+\alpha h_{sd}) \approx f(x) + \alpha J(x)h_{sd}，\alpha为步长，h_{sd}为最速下降的梯度。对近似后的式子进行最小二乘构建：

\frac{1}{2}\left \| f(x) + \alpha Jh_{sd}\right \|^{2}

        上式展开对h_{sd}求导，得到：\alpha；

 再考虑GN的迭代优化，这样在优化的时候增量就有两种取值： a = h_{gn}和b = \alpha h_{sd}；

令c = a^{T}(b-a)，则\beta更新如下：

增量更新的伪代码：（\Delta是置信区域）

      Dog-Leg实际上就是在高斯牛顿解在限制范围内的时候，采用它的解；不在的时候就要结合一阶梯度下降去考虑解，总之，要把这个解控制在范围内或者范围的边界上；

code：

int iteratorNum = 100;	// 迭代次数
	for(int i = 1; i<=iteratorNum; i++) {

		for (int j = 0; j< Sample_NUM; ++j) {		// 构造方程
			Jacb_abc.resize(Sample_NUM, 3);
			error_i.resize(Sample_NUM, 1);

			double y_est = exp( aft_abc(0) * x_set.at(j) * x_set.at(j) + 	\
													aft_abc(1) * x_set.at(j) + aft_abc(2));
			// 雅克比  对待优化变量的偏导 注意真实的J应该是
			Jacb_abc(j,0) =   -x_set.at(j) * x_set.at(j) * y_est;
			Jacb_abc(j,1) =   			    -x_set.at(j) * y_est;
			Jacb_abc(j,2) = 					    -1.0 * y_est;
		
			// 误差
			error_i(j, 0) = y_set.at(j) - y_est;
		}	
		// 计算增量方程 H * delta_? = g	
		H = Jacb_abc.transpose() * Jacb_abc;		// 计算H
		g = -Jacb_abc.transpose() * error_i; 		// 计算g
	
		// 计算alpha 
		alpha = pow( g.lpNorm<1>(), 2) / pow( (Jacb_abc*g).lpNorm<1>(), 2);   

		// 解h_sd
		h_sd = -alpha * g;	

		// 解gn
		h_gn = H.ldlt().solve(g);  

		// 计算beta
		Eigen::Vector3d param_a = alpha * h_sd;		// a
		Eigen::Vector3d param_b = h_gn;				// b
		double param_c = param_a.transpose() * (param_b - param_a);
		if (param_c<=0) {

			beta = (sqrt( pow(param_c,2) + pow((param_b-param_a).lpNorm<1>(), 2)  *
									( pow(u,2)- pow(param_a.lpNorm<1>(),2) ) ) - c) / 
													pow((param_b-param_a).lpNorm<1>(), 2);
		}else {

			beta = ( pow(u,2)- pow(param_a.lpNorm<1>(),2) ) / 
							(sqrt( pow(param_c,2) + pow((param_b-param_a).lpNorm<1>(), 2) *
									( pow(u,2)- pow(param_a.lpNorm<1>(),2) ) ) + param_c);
		}

		// 计算h_dl
		if ( param_b.lpNorm<1>() <= u ){		// 高斯解在约束内，用高斯
			h_dl = param_b;
		}else if ( param_a.lpNorm<1>() >= u) {		// 高斯解在约束外，最速也在约束外，用最速（更改步进）
			h_dl = ( u/h_sd.lpNorm<1>() ) * h_sd; 
		} else { 
			h_dl = param_a + beta * (param_b - param_a); 	// 高斯解在约束外， 最速也在约束内，融合
		}

		// 误差平方和
		curSquareCost = 1.0f/2 * error_i.squaredNorm();
	
		// 判断是否提前收敛
		if ( error_i.lpNorm<Eigen::Infinity>() < 1e-6 ||  
					u < 1e-6 * (aft_abc.lpNorm<1>()+1e-6) || 
						g.lpNorm<Eigen::Infinity>() < 1e-6)  { 

			std::cout << "   真实abc: " << a << " " << b << " " << c << std::endl;
			std::cout << "   迭代结束! "  << std::endl;
			std::cout << "迭代结果abc: " << aft_abc.transpose() << std::endl;
			return 0; 
		}

		// 求一阶泰勒近似度
		error_sum_aft.resize(Sample_NUM, 1);
		for (int k = 0; k<Sample_NUM; k++) { 
			error_sum_aft(k,0) = y_set.at(k) - exp( (aft_abc(0)+h_dl(0)) * x_set.at(k) * x_set.at(k) + 	\
													(aft_abc(1)+h_dl(1)) * x_set.at(k) + (aft_abc(2)+h_dl(2)) );
		}	
		// curSquareCost_aft = 1.0f/2*(error_sum_aft.transpose() * error_sum_aft)(0,0);
		curSquareCost_aft = 1.0f/2 * error_sum_aft.squaredNorm();		// 元素平方和


		Eigen::MatrixXd L0_Ldelta = -h_dl.transpose() * Jacb_abc.transpose() * error_i - 1.0f/2 * h_dl.transpose() * Jacb_abc.transpose() * Jacb_abc * h_dl;
		Eigen::MatrixXd L0_Ldelta2 = 1.0f/2 * h_dl.transpose() * ( u*h_dl + g);  
		Eigen::MatrixXd L0_Ldelta3 = 1.0/2*((Jacb_abc*h_dl).transpose() * (Jacb_abc*h_dl));
		
		taylar_similary = (curSquareCost-curSquareCost_aft) / L0_Ldelta(0,0); 
		// 信赖域更新法则
		if (taylar_similary>0) { 	
			// 更新增量
			aft_abc += h_dl;		
		}

		if (taylar_similary>0.75) {

			u = std::max<double>(u, 3.0*h_dl.lpNorm<1>() );	
		} else if (taylar_similary<0.25) { 

			u = u/2.0;	
		} else {

			u = u;
		}


		if (i%1==0) 
		{
			std::cout << "   泰勒近似: " << taylar_similary << std::endl;
			std::cout << "   本次增量: " << h_dl.transpose() << std::endl;
			std::cout << "当前迭代次数: " << i << "/" << iteratorNum << "     当前总误差: " << curSquareCost << std::endl<< std::endl;
		}	

	}

 迭代估计的结果，效果还是不错的：（11次收敛）

         在实际调试的过程中，很多时候会遇到高斯牛顿无法收敛，刚开始怀疑代码写的有问题，直到使用了g2o上面高斯牛顿也出现发散，反复分析了几次，才相信自己写的没毛病，纯粹的高斯牛顿需要良好的初值去防止它陷入局部解的问题，不然很容易出现病态的H矩阵导致不收敛。。。累死zz。。。

优化问题求解步骤：
1）确定优化方程（误差方程）
2）确定优化变量
3）求解雅克比J：误差方程对优化变量的偏导
4）构建增量方程
5）矩阵分解法求解

Last，优化问题都依赖一个良好的初值！！！！！！！！！！！！！

评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值