高等数学入门教程 — 极限

一、引子

例. 假设银行的利息率与存钱时间成正比，即$n=\lambda t$，问将钱存入银行时间$T$后获得的利息率最大为多少。

如果直接存$T$时间，那么利息率为$\lambda T$。但是如果先存一段时间，取出来，将本金与利息再存入银行，最后得到的总利息率会不会高呢？

假设总共存$m$次，则总利息率为$n=f(m)=(1+\lambda T/m{)}^m-1$。画出图像为：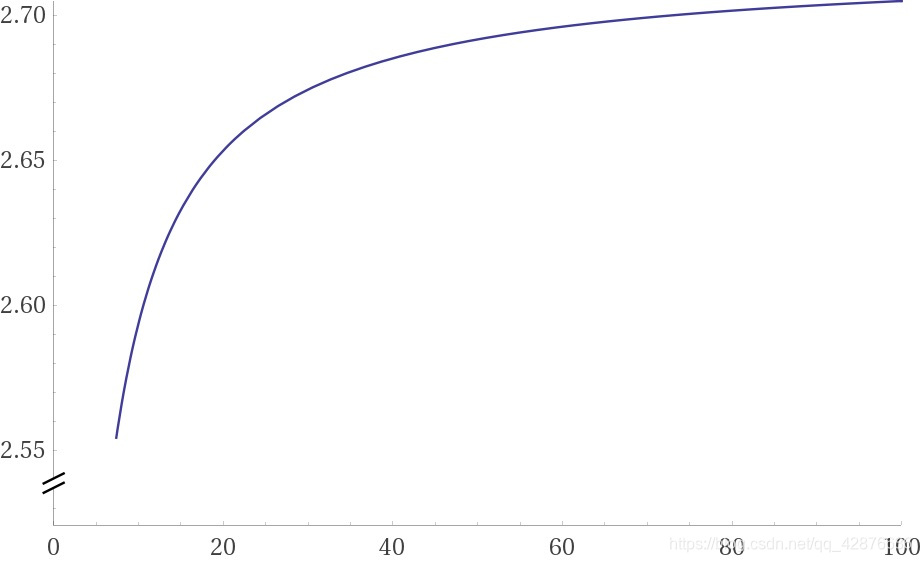
观察到$m$增大时，$f(m)$增大，但是$f(m)$并不能任意增大，似乎有一个上界，大约是$2.7$。但是$f(m)$是没有最大值的，因为如果$f(m_0)$为最大值，那么$f(m_0+1)>f(m_0)$为更大的数，这是矛盾的。这就导致了一个问题，从图像上可以看出$f(m)$有一个约为$2.7$的上阶，但是$f(m)$却没有最大值，也就是说，似乎没有办法准确地求出这个上界。要解决这个问题，必须使用极限的思想，也就是让$m\to \infty$。

类似的例子有很多，比如函数$f(x)=x^x$。$f(0)$是没有定义的，但是当$x\to 0$的时候，$f(x)\to 1$，如图：

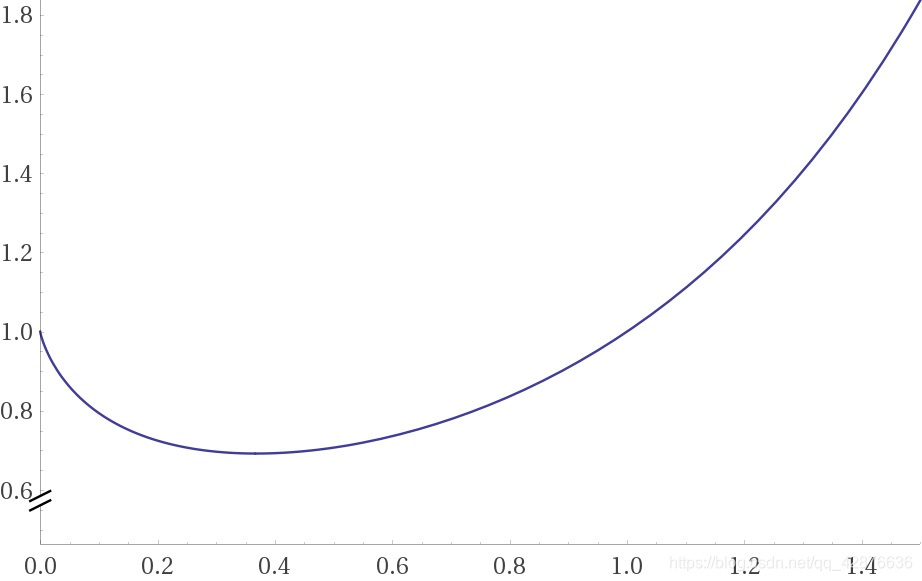
这就启发我们，研究函数的时候，光研究定义域内的点是不行的，有时候定义域外的点也有研究价值。这就需要极限。

二、极限的定义

明白了极限的意义后，就需要对极限有一个数学上严格的定义，因为光靠感觉定义出来的东西是不严谨的，必须用数学化的语言去定义。下面是极限的标准定义：

设$f(x)$在$x_0$的去心领域$I$上有定义，如果$c$满足，对于任意给定正数$\delta$，均存在正数$\epsilon$，使得对于任意$x$满足$0<|x-x_0|<\epsilon$，均有$|f(x)-c|<\delta$，则称$f(x)$在$x\to x_0$的极限为$c$，记作$$\underset{x\to x_0}{\lim }f(x)=c$$

设$f(x)$在$x_0$的去心领域$I$上有定义，如果$c$满足，对于任意给定$\delta$，均存在$\epsilon$，使得对于任意$x$满足$0<x-x_0<\epsilon$，均有$|f(x)-c|<\delta$，则称$f(x)$在$x\to x_0$的右极限为$c$，记作$$\underset{{x\to x_0}^{+}}{\lim }f(x)=c$$

设$f(x)$在$x_0$的去心领域$I$上有定义，如果$c$满足，对于任意给定$\delta$，均存在$\epsilon$，使得对于任意$x$满足$0<x_0-x<\epsilon$，均有$|f(x)-c|<\delta$，则称$f(x)$在$x\to x_0$的左极限为$c$，记作$$\underset{{x\to x_0}^{-}}{\lim }f(x)=c$$

如果直接研究这三个定义，可能会比较吃力。现在我用通俗的语言解释着三个定义。在第一个定义中，$x_0$和$c$都类似于基准点，而$\epsilon$和$\delta$都类似于精度。这个定义的意思是，给定任何一个需要达到的精度$\delta$(即$f(x)$与$c$的差的绝对值)，都能找到一个$\epsilon$，使得在$x_0$左右这么小的范围内，$f(x)$均在$\delta$精度内。也就是说，当不断缩小$f(x)$的范围的时候，总能通过缩小$x$的范围，使得$f(x)$落在给定的范围内。不难发现，这个定义非常严谨，同时也能准确地表示出极限本身的含义。

后面两个定义是对第一个定义的补充，因为有时候$x$从两边接近$x_0$时，$f(x)$的极限时不一样的，因此需要规定左极限和右极限。

如果函数在一个点的左极限与右极限不相等，那么函数在这个点上极限不存在。

如果函数在一个点趋近于正无穷大(或负无穷大)，那么函数在这个点的极限不存在，但是在本教程中写作极限为正无穷大(或负无穷大)。

例1 证明：（1）${\lim }_{x\to 1}x=1$ （2）$li{m}_{x\to 1}{x}^2=1$ （3） lim ⁡ x → 1 1 x = 1 \lim_{x\rightarrow1}\frac1x=1 lim